5.2 Expectativa condicional individual (ICE)
Los gráficos de Expectativas condicionales individuales (ICE) muestran una línea por instancia, que muestra cómo cambia la predicción de esa observación cuando cambia una característica.
El gráfico de dependencia parcial para el efecto promedio de una característica es un método global porque no se enfoca en observaciones específicas, sino en un promedio general. El equivalente a un PDP para instancias de datos individuales se llama gráfico de expectativa condicional individual (ICE) (Goldstein et al. 2017 28). Un gráfico ICE visualiza la dependencia de la predicción en una característica para cada instancia por separado, lo que da como resultado una línea por instancia, en comparación con una línea general en los gráficos de dependencia parcial. Un PDP es el promedio de las líneas de un diagrama ICE. Los valores para una observación se pueden calcular manteniendo todas las otras características iguales, creando variantes de esta instancia reemplazando el valor de la característica con valores de una cuadrícula y haciendo predicciones con el modelo de caja negra para estas instancias recién creadas. El resultado es un conjunto de puntos para una observación con el valor de la característica de la cuadrícula y las predicciones respectivas.
¿Cuál es el punto de mirar las expectativas individuales en lugar de las dependencias parciales? Las gráficas de dependencia parcial pueden oscurecer una relación heterogénea creada por las interacciones. Los PDP pueden mostrarte cómo se ve la relación promedio entre una característica y la predicción. Esto solo funciona bien si las interacciones entre las características para las cuales se calcula el PDP y las otras características son débiles. En caso de interacciones, la trama ICE proporcionará mucha más información.
Una definición más formal: En las gráficas ICE, para cada instancia en \(\{(x_{S}^{(i)},x_{C}^{(i)})\}_{i=1}^N\) la curva \(\hat{f}_S^{(i)}\) se representa frente a \(x^{(i)}_{S}\), mientras que \(x^{(i)}_{C}\) permanece fijo.
5.2.1 Ejemplos
Volvamos al conjunto de datos de cáncer cervical y veamos cómo la predicción de cada instancia está asociada con la función “Edad”. Analizaremos un random forest que predice la probabilidad de cáncer para una mujer dados los factores de riesgo. En el gráfico de dependencia parcial hemos visto que la probabilidad de cáncer aumenta alrededor de los 50 años, pero ¿es esto cierto para todas las mujeres en el conjunto de datos? El gráfico ICE revela que para la mayoría de las mujeres el efecto de la edad sigue el patrón promedio de un aumento a los 50 años, pero hay algunas excepciones: Para las pocas mujeres que tienen una alta probabilidad pronosticada a una edad temprana, la probabilidad pronosticada de cáncer no cambia mucho con la edad.
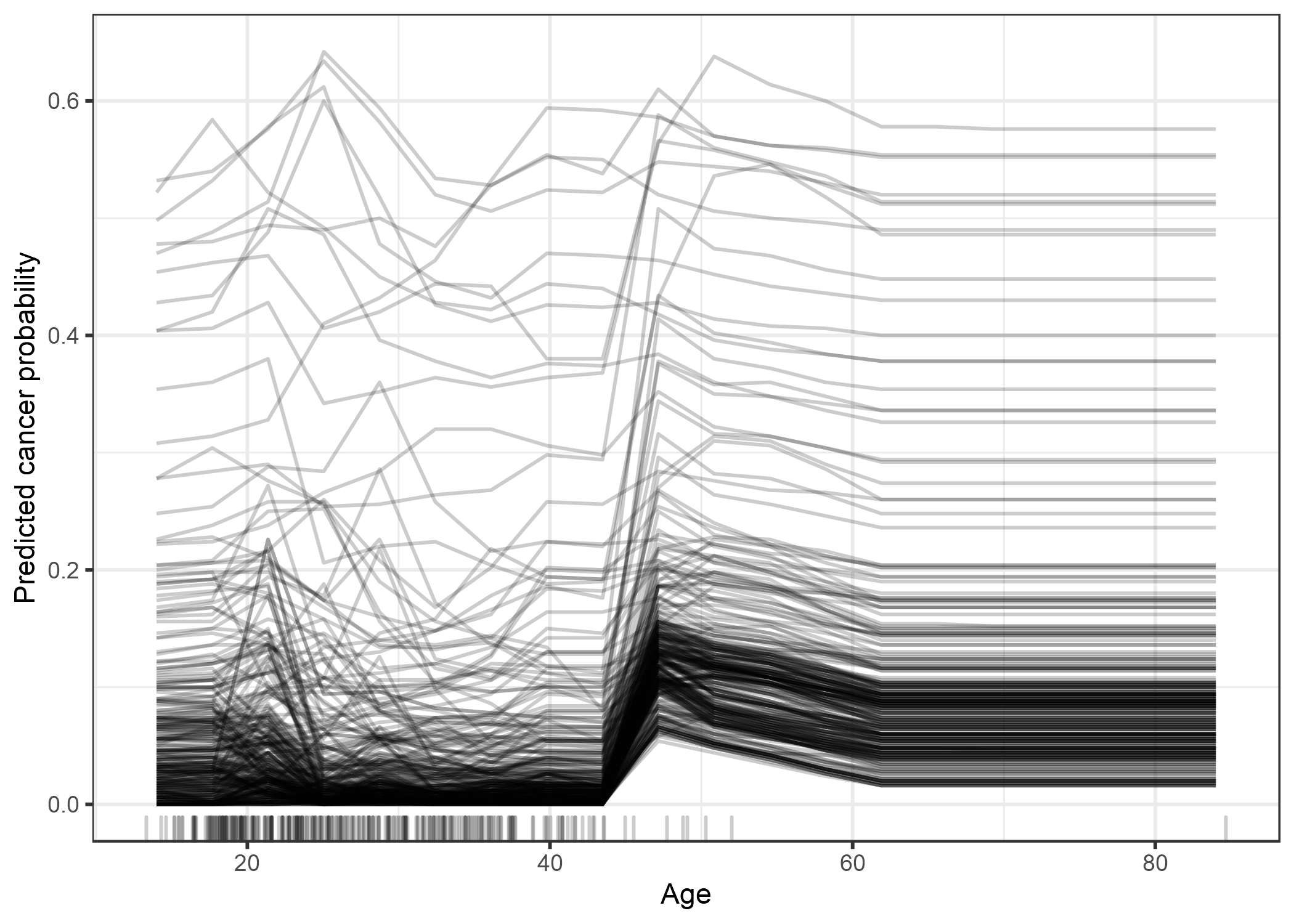
FIGURA 5.6: Gráfico ICE de probabilidad de cáncer cervical por edad. Cada línea representa a una mujer. Para la mayoría de las mujeres hay un aumento en la probabilidad pronosticada de cáncer al aumentar la edad. Para algunas mujeres con un pronóstico probabilidad de cáncer por encima de 0.4, la predicción no cambia mucho a mayor edad.
La siguiente figura muestra las gráficas de ICE para la predicción de alquiler de bicicletas. El modelo de predicción subyacente es un random forest.
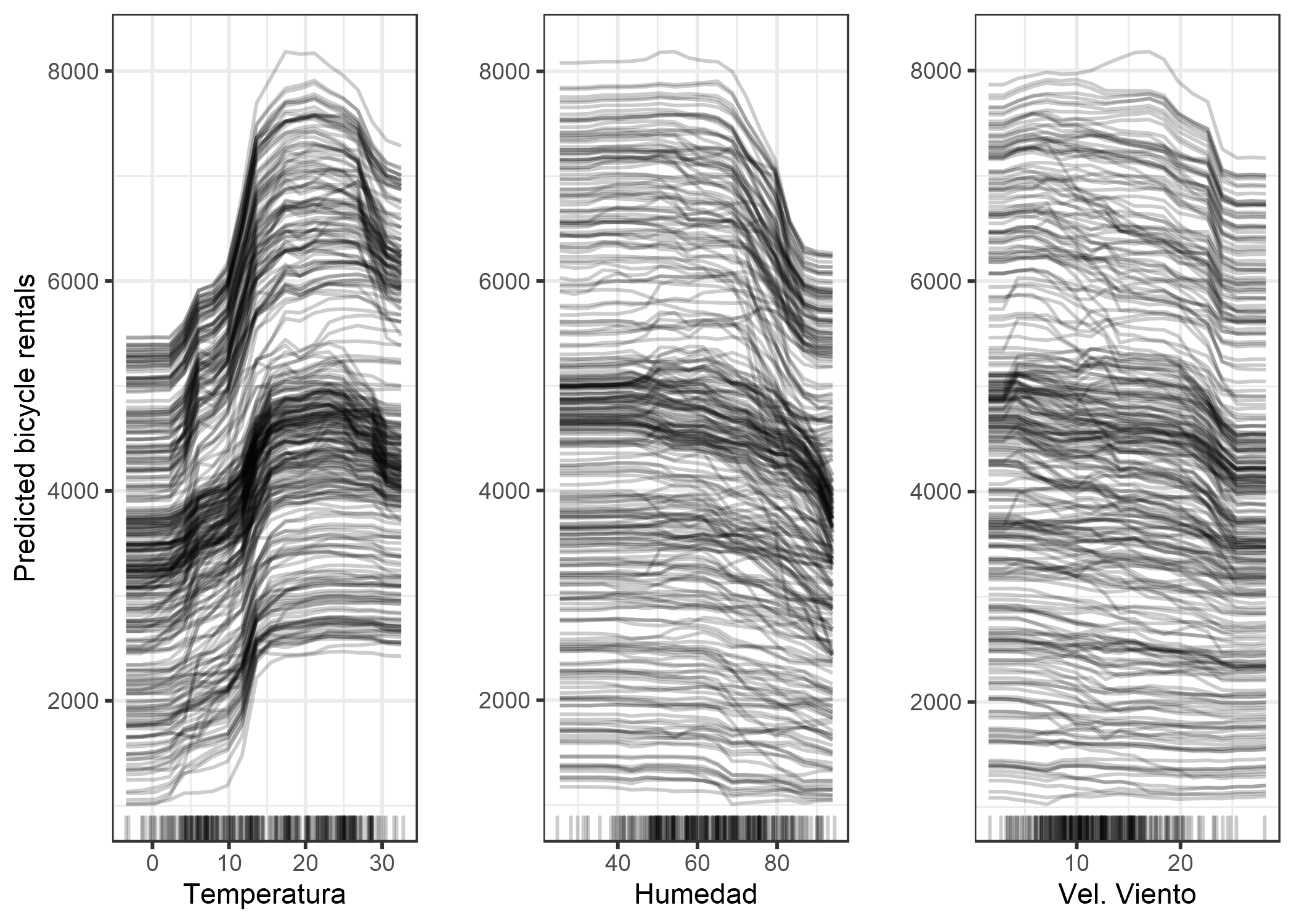
FIGURA 5.7: Gráfico ICE para el alquiler de bicicletas previsto por las condiciones climáticas. Se pueden observar los mismos efectos que en los gráficos de dependencia parcial.
Todas las curvas parecen seguir el mismo curso, por lo que no hay interacciones obvias. Eso significa que el PDP es un buen resumen de las relaciones entre las características mostradas y el número previsto de bicicletas.
5.2.1.1 Gráfico ICE centrado
Hay un problema con los gráficos de ICE: A veces puede ser difícil saber si las curvas ICE difieren entre los individuos porque comienzan con diferentes predicciones. Una solución simple es centrar las curvas en un cierto punto de la entidad y mostrar solo la diferencia en la predicción hasta este punto. La gráfica resultante se llama gráfica centrada de ICE (c-ICE). Anclar las curvas en el extremo inferior de la entidad es una buena opción. Las nuevas curvas se definen como:
\[\hat{f}_{cent}^{(i)}=\hat{f}^{(i)}-\mathbf{1}\hat{f}(x^{a},x^{(i)}_{C})\]
donde \(\mathbf{1}\) es un vector de 1 con el número apropiado de dimensiones (generalmente una o dos), \(\hat{f}\) es el modelo ajustado y xa es el punto de anclaje.
5.2.1.2 Ejemplo
Por ejemplo, tome la gráfica ICE del cáncer de cuello uterino para la edad y centre las líneas en la edad más joven observada:
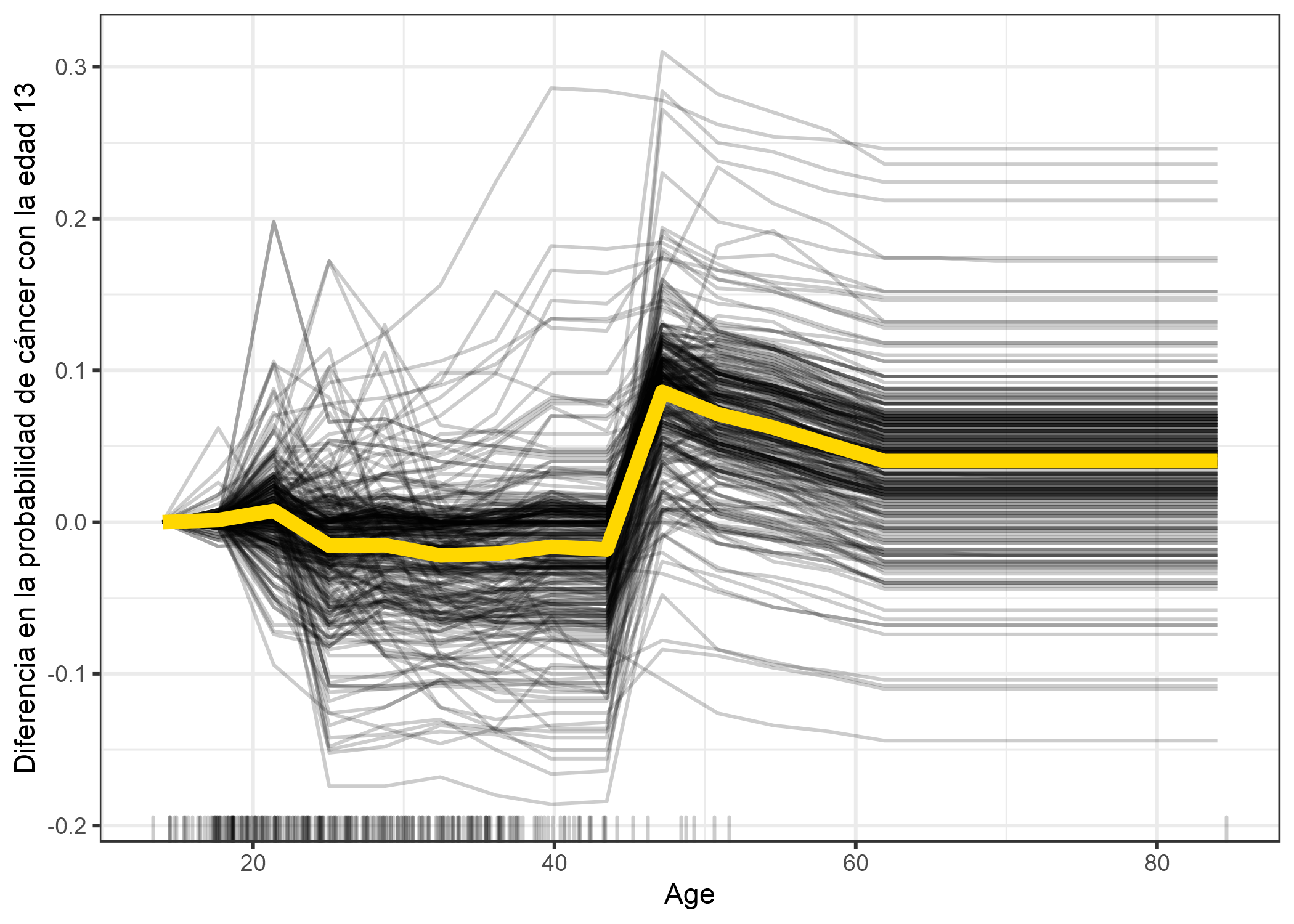
FIGURA 5.8: Gráfico ICE centrado para la probabilidad pronosticada de cáncer por edad. Las líneas se fijan en 0 a la edad 14. En comparación con la edad 14, las predicciones para la mayoría de las mujeres permanecen sin cambios hasta la edad de 45 años, donde aumenta la probabilidad pronosticada.
Las gráficas centradas de ICE facilitan la comparación de las curvas de instancias individuales. Esto puede ser útil si no queremos ver el cambio absoluto de un valor predicho, sino la diferencia en la predicción en comparación con un punto fijo del rango de características.
Echemos un vistazo al gráfico centrado ICE para la predicción del alquiler de bicicletas:
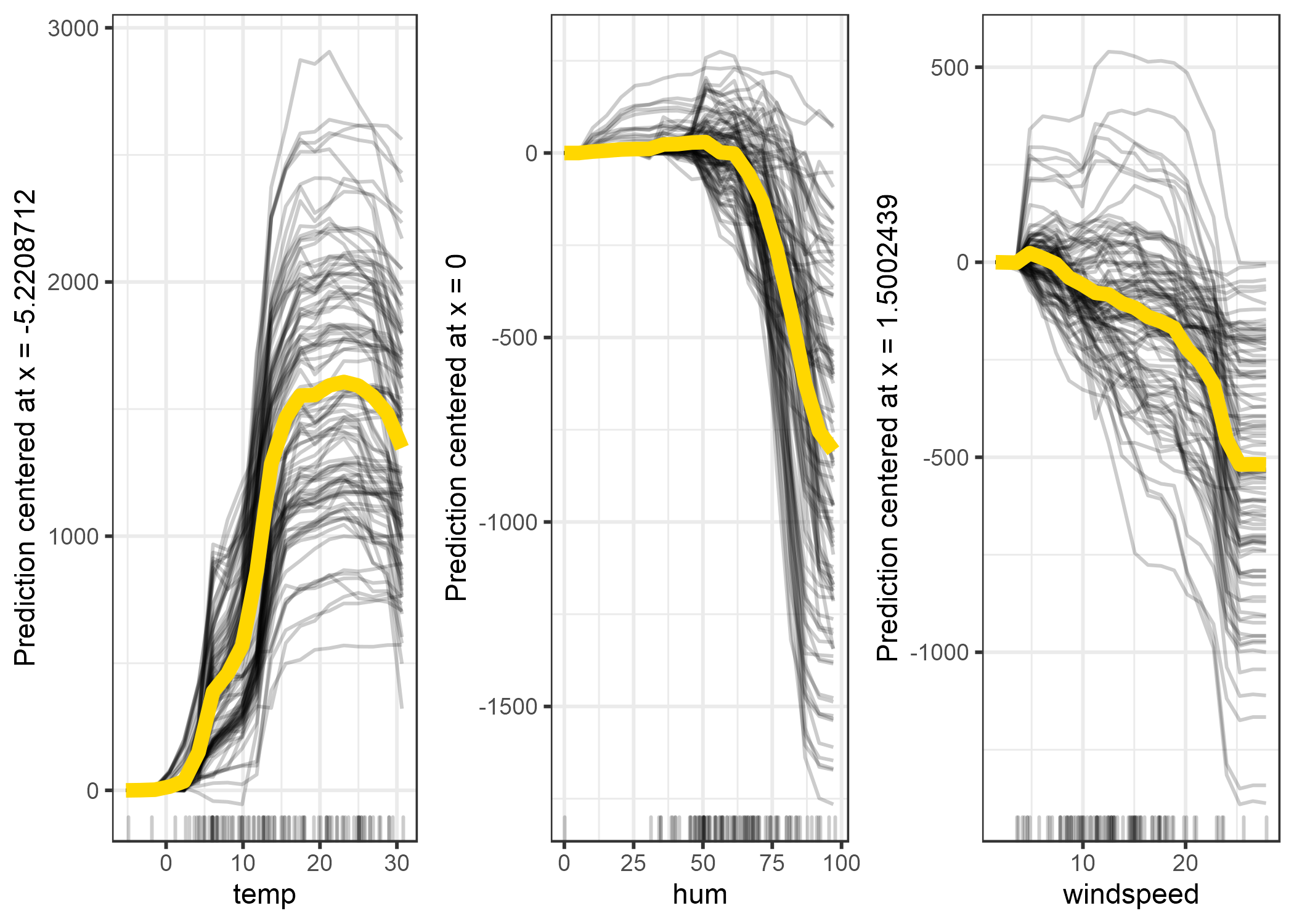
FIGURA 5.9: Gráfico ICE centrado ICE del número previsto de bicicletas por condición climática. Las líneas muestran la diferencia en la predicción en comparación con la predicción con el valor de la característica respectiva en su mínimo observado.
5.2.1.3 Diagrama de ICE derivado
Otra forma de hacer que sea visualmente más fácil detectar la heterogeneidad es observar las derivadas individuales de la función de predicción con respecto a una característica. El diagrama resultante se llama diagrama derivado de ICE (d-ICE). Las derivadas de una función (o curva) te indican si ocurren cambios y en qué dirección ocurren. Con el diagrama ICE derivado, es fácil detectar rangos de valores de características donde las predicciones de caja negra cambian para (al menos algunas) instancias. Si no hay interacción entre la característica analizada \(x_S\) y las otras características \(x_C\), la función de predicción se puede expresar como:
\[\hat{f}(x)=\hat{f}(x_S,x_C)=g(x_S)+h(x_C),\quad\text{con}\quad\frac{\delta\hat{f}(x)}{\delta{}x_S}=g'(x_S)\]
Sin interacciones, las derivadas parciales individuales deberían ser las mismas para todas las instancias. Si difieren, se debe a interacciones y se hace visible en el diagrama d-ICE. Además de mostrar las curvas individuales para la derivada de la función de predicción con respecto a la función en S, mostrar la desviación estándar de la derivada ayuda a resaltar regiones en función en S con heterogeneidad en las derivadas estimadas. El diagrama derivado de ICE tarda mucho tiempo en calcularse y es poco práctico.
5.2.2 Ventajas
Las curvas de expectativas condicionales individuales son aún más intuitivas de entender que las gráficas de dependencia parcial. Una línea representa las predicciones para una instancia si variamos la característica de interés.
A diferencia de los gráficos de dependencia parcial, las curvas ICE pueden descubrir relaciones heterogéneas.
5.2.3 Desventajas
Las curvas ICE solo pueden mostrar una característica de manera significativa, porque dos características requerirían el dibujo de varias superficies superpuestas y no vería nada en la gráfica.
Las curvas ICE sufren el mismo problema que las PDP: Si la característica de interés está correlacionada con las otras características, entonces algunos puntos en las líneas podrían ser puntos de datos no válidos de acuerdo con la distribución conjunta de características.
Si se dibujan muchas curvas ICE, la trama puede estar superpoblada y no verás nada. La solución: agrega algo de transparencia a las líneas o dibuje solo una muestra de las líneas.
En los gráficos de ICE puede que no sea fácil ver el promedio. Esto tiene una solución simple: Combina las curvas de expectativa condicional individuales con la gráfica de dependencia parcial.
5.2.4 Software y alternativas
Las gráficas ICE se implementan en los paquetes R iml (utilizado para estos ejemplos), ICEbox 29 y pdp.
Otro paquete R que hace algo muy similar a ICE es condvis.