4.5 Reglas de decisión

Una regla de decisión es una simple declaración SI-ENTONCES (IF-THEN) que consiste en una condición (también llamada antecedente) y una predicción. Por ejemplo: SI llueve Y SI es abril (condición), ENTONCES lloverá mañana (predicción). Se puede usar una sola regla de decisión o una combinación de varias reglas para hacer predicciones.

Las reglas de decisión siguen una estructura general: SI se cumplen las condiciones, ENTONCES haga una cierta predicción. Las reglas de decisión son probablemente los modelos de predicción más interpretables. Su estructura SI-ENTONCES se asemeja semánticamente al lenguaje natural y a la forma en que pensamos, siempre que la condición se construya a partir de características inteligibles, la duración de la condición sea corta (pequeño número de pares característica = valor combinados con un Y) y hay no demasiadas reglas. En programación, es muy natural escribir reglas SI-ENTONCES. Lo nuevo en el aprendizaje automático es que las reglas de decisión se aprenden a través de un algoritmo.

Imagina usar un algoritmo para aprender las reglas de decisión para predecir el valor de una casa (bajo, medio o alto). Una regla de decisión aprendida por este modelo podría ser: Si una casa es más grande que 100 metros cuadrados y tiene un jardín, entonces su valor es alto. Más formalmente: SI tamaño>100 Y jardín=1 ENTONCES valor = alto.

Analicemos la regla de decisión:

• tamaño>100 es la primera condición en la parte SI.
• jardín = 1 es la segunda condición en la parte SI.
• Las dos condiciones están conectadas con un ‘Y’ para crear una nueva condición. Ambas deben ser ciertas para que se aplique la regla.
• El resultado previsto (ENTONCES) es valor = alto.

Una regla de decisión utiliza al menos una declaración característica = valor en la condición, sin límite superior de cuántas más se pueden agregar con un ‘AND’. Una excepción es la regla predeterminada que no tiene una parte IF explícita y que se aplica cuando no se aplica ninguna otra regla, pero veremos más sobre esto más adelante.

La utilidad de una regla de decisión generalmente se resume en dos números: Soporte y precisión.

Soporte o cobertura de una regla: El porcentaje de instancias a las que se aplica la condición de una regla se denomina soporte. Tomemos, por ejemplo, la regla tamaño = grande Y ubicación = buena ENTONCES valor = alto para predecir los valores de la casa. Suponga que 100 de 1000 casas son grandes y están en una buena ubicación, entonces el respaldo de la regla es del 10%. La predicción (ENTONCES) no es importante para el cálculo del soporte.

Precisión o confianza de una regla: La precisión de una regla es una medida de cuán precisa es la regla para predecir la clase correcta para las instancias a las que se aplica la condición de la regla. Por ejemplo: Digamos de las 100 casas, donde la regla tamaño = grande Y ubicación = buena ENTONCES valor = alto, 85 tienen valor = alto, 14 tienen valor = medio y 1 tiene valor = bajo, entonces la precisión de la regla es del 85%.

Por lo general, existe una compensación entre precisión y soporte: Al agregar más funciones a la condición, podemos lograr una mayor precisión, pero perdemos soporte.

Para crear un buen clasificador para predecir el valor de una casa, es posible que necesites aprender no solo una regla, sino tal vez 10 o 20. Entonces las cosas pueden complicarse y puedes encontrarte con uno de los siguientes problemas:

• Las reglas pueden superponerse: ¿Qué sucede si quiero predecir el valor de una casa y se aplican dos o más reglas y me dan predicciones contradictorias?
• No se aplica ninguna regla: ¿Qué sucede si quiero predecir el valor de una casa y no se aplica ninguna de las reglas?

Hay dos estrategias principales para combinar varias reglas: Listas de decisiones (ordenadas) y conjuntos de decisiones (sin ordenar). Ambas estrategias implican diferentes soluciones al problema de la superposición de reglas.

Una lista de decisiones introduce un orden en las reglas de decisión. Si la condición de la primera regla es verdadera para una instancia, usamos la predicción de la primera regla. Si no, pasamos a la siguiente regla y verificamos si corresponde y así sucesivamente. Las listas de decisiones resuelven el problema de la superposición de reglas al devolver solo la predicción de la primera regla de la lista que se aplica.

Un conjunto de decisiones se asemeja a una democracia de las reglas, excepto que algunas reglas pueden tener un mayor poder de voto. En un conjunto, las reglas son mutuamente excluyentes o hay una estrategia para resolver conflictos, como la votación por mayoría, que puede ser ponderada por la precisión de las reglas individuales u otras medidas de calidad. La interpretabilidad sufre potencialmente cuando se aplican varias reglas.

Tanto las listas de decisiones como los conjuntos pueden sufrir el problema de que ninguna regla se aplica a una instancia. Esto se puede resolver mediante la introducción de una regla predeterminada. La regla predeterminada es la regla que se aplica cuando no se aplica ninguna otra regla. La predicción de la regla predeterminada suele ser la clase más frecuente de los puntos de datos que no están cubiertos por otras reglas. Si un conjunto o una lista de reglas cubre todo el espacio de características, lo llamamos exhaustivo. Al agregar una regla predeterminada, un conjunto o lista se vuelve exhaustivo automáticamente.

Hay muchas maneras de aprender reglas de los datos y este libro está lejos de abarcarlas todas. Este capítulo te muestra tres de ellos. Los algoritmos se eligen para cubrir una amplia gama de ideas generales para reglas de aprendizaje, por lo que los tres representan enfoques muy diferentes.

1. OneR aprende las reglas de una sola característica. OneR se caracteriza por su simplicidad, interpretabilidad y su uso como punto de referencia.
2. La cobertura secuencial es un procedimiento general que aprende de forma iterativa las reglas y elimina los puntos de datos cubiertos por la nueva regla. Este procedimiento es utilizado por muchos algoritmos de aprendizaje de reglas.
3. Listas de reglas bayesianas combinan patrones frecuentes previamente minados en una lista de decisiones utilizando estadísticas bayesianas. El uso de patrones minados es un enfoque común utilizado por muchos algoritmos de aprendizaje de reglas.

Comencemos con el enfoque más simple: usar la mejor característica para aprender reglas.

4.5.1 Aprender las reglas de una sola función (OneR)

El algoritmo OneR sugerido por Holte (1993)¹⁸ es uno de los algoritmos de inducción de reglas más simples. De todas las características, OneR selecciona la que lleva más información sobre el resultado de interés y crea reglas de decisión a partir de esta característica.

A pesar del nombre OneR, que significa “Una regla”, el algoritmo genera más de una regla: En realidad, es una regla por valor de característica única de la mejor característica seleccionada. Un mejor nombre sería OneFeatureRules.

El algoritmo es simple y rápido:

1. Discretiza las características continuas eligiendo los intervalos apropiados.
2. Para cada característica:
   • Crea una tabla cruzada entre los valores de la característica y el resultado (categórico).
   • Para cada valor de la característica, crea una regla que prediga la clase más frecuente de las instancias que tienen este valor de característica particular (puede leerse en la tabla cruzada).
   • Calcula el error total de las reglas para la función.
3. Selecciona la función con el error total más pequeño.

OneR siempre cubre todas las instancias del conjunto de datos, ya que utiliza todos los niveles de la función seleccionada. Los valores faltantes pueden tratarse como un valor de característica adicional o imputarse de antemano.

Un modelo OneR es un árbol de decisión con una sola división. La división no es necesariamente binaria como en CART, sino que depende del número de valores de características únicas.

Veamos un ejemplo de cómo OneR elige la mejor característica. La siguiente tabla muestra un conjunto de datos artificiales sobre casas con información sobre su valor, ubicación, tamaño y si se permiten mascotas. Estamos interesados en aprender un modelo simple para predecir el valor de una casa.

ubicación	tamaño	mascotas	valor
bueno	pequeño	sí	alto
bueno	grande	no	alto
bueno	grande	no	alto
malo	mediano	no	medio
bueno	mediano	solo gatos	medio
bueno	pequeño	solo gatos	medio
malo	mediano	sí	medio
malo	pequeño	sí	bajo
malo	mediano	sí	bajo
malo	pequeño	no	bajo

OneR crea las tablas cruzadas entre cada característica y el resultado:

	valor=bajo	valor=medio	valor=alto
ubicación=bueno	0	2	3
ubicación=malo	3	2	0

	valor=bajo	valor=medio	valor=alto
tamaño=grande	0	0	2
tamaño=mediano	1	3	0
tamaño=pequeño	2	1	1

	valor=bajo	valor=medio	valor=alto
mascotas=no	1	1	2
mascotas=sí	2	1	1
mascotas=solo gatos	0	2	0

Para cada característica, revisamos la tabla fila por fila: Cada valor de característica es la parte SI de una regla; La clase más común para las instancias con este valor de característica es la predicción, la parte ENTONCES de la regla. Por ejemplo, la función de tamaño con los niveles pequeño,mediano y grande da como resultado tres reglas. Para cada característica calculamos la tasa de error total de las reglas generadas, que es la suma de los errores. La función de ubicación tiene los valores posibles malo ybueno. El valor más frecuente para las casas en ubicaciones malas es bajo y cuando usamosbajo como predicción, cometemos dos errores, porque dos casas tienen un valor medio. El valor predicho de las casas en buenas ubicaciones es alto y nuevamente cometemos dos errores, porque dos casas tienen un valormedio. El error que cometemos al usar la función de ubicación es 4/10, para la función de tamaño es 3/10 y para la función de mascota es 4/10. La función de tamaño produce las reglas con el error más bajo y se utilizará para el modelo final de OneR:

SI tamaño = chico ENTONCES valor = bajo SI tamaño = medio ENTONCES value = medio SItamaño = grandeENTONCESvalue = grande`

OneR prefiere características con muchos niveles posibles, porque esas características pueden sobreajustar el objetivo más fácilmente. Imagina un conjunto de datos que contiene solo ruido y ninguna señal, lo que significa que todas las características toman valores aleatorios y no tienen un valor predictivo para el objetivo. Algunas características tienen más niveles que otras. Las características con más niveles ahora pueden adaptarse más fácilmente. Una característica que tiene un nivel separado para cada instancia de los datos predeciría perfectamente todo el conjunto de datos de entrenamiento. Una solución sería dividir los datos en conjuntos de entrenamiento y validación, aprender las reglas sobre los datos de entrenamiento y evaluar el error total para elegir la función en el conjunto de validación.

Los lazos son otro problema, es decir, cuando dos características dan como resultado el mismo error total. OneR resuelve los lazos al tomar la primera característica con el error más bajo o la que tiene el valor p más bajo de una prueba de chi-cuadrado.

Ejemplo

Probemos OneR con datos reales. Utilizamos la tarea de clasificación de cáncer cervical para probar el algoritmo OneR. Todas las características de entrada continua se discretizaron en sus 5 cuantiles. Se crean las siguientes reglas:

Age	prediction
(12.9,27.2]	Healthy
(27.2,41.4]	Healthy
(41.4,55.6]	Healthy
(55.6,69.8]	Healthy
(69.8,84.1]	Healthy

OneR eligió la función de edad como la mejor función predictiva. Dado que el cáncer es raro, para cada regla la clase mayoritaria y, por lo tanto, la etiqueta predicha es siempre Saludable, lo cual es bastante inútil. No tiene sentido usar la predicción de etiqueta en este caso desequilibrado. La tabla cruzada entre los intervalos de ‘Edad’ y Cáncer/Saludable junto con el porcentaje de mujeres con cáncer es más informativa:

	# Cancer	# Healthy	P(Cancer)
Age=(12.9,27.2]	26	477	0.05
Age=(27.2,41.4]	25	290	0.08
Age=(41.4,55.6]	4	31	0.11
Age=(55.6,69.8]	0	1	0.00
Age=(69.8,84.1]	0	4	0.00

Pero antes de comenzar a interpretar: Dado que la predicción para cada característica y cada valor es Saludable, la tasa de error total es la misma para todas las características. Los vínculos en el error total se resuelven, de manera predeterminada, utilizando la primera función de las que tienen las tasas de error más bajas (aquí, todas las funciones tienen 55/858), que resulta ser la característica Edad.

OneR no admite tareas de regresión. Pero podemos convertir una tarea de regresión en una tarea de clasificación cortando el resultado continuo en intervalos. Utilizamos este truco para predecir el número de bicicletas alquiladas con OneR cortando el número de bicicletas en sus cuatro cuartiles (0-25%, 25-50%, 50-75% y 75-100%) La siguiente tabla muestra la función seleccionada después de ajustar el modelo OneR:

mnth	prediction
JAN	[22,3152]
FEB	[22,3152]
MAR	[22,3152]
APR	(3152,4548]
MAY	(5956,8714]
JUN	(4548,5956]
JUL	(5956,8714]
AUG	(5956,8714]
SEP	(5956,8714]
OKT	(5956,8714]
NOV	(3152,4548]
DEZ	[22,3152]

La función seleccionada es el mes. La función de mes tiene (¡sorpresa!) 12 niveles de funciones, que es más que la mayoría de las otras funciones. Por lo tanto, existe el peligro de sobreajustar. En el lado más optimista: la función del mes puede manejar la tendencia estacional (por ejemplo, bicicletas menos alquiladas en invierno) y las predicciones parecen ser sensatas.

Ahora pasamos del simple algoritmo OneR a un procedimiento más complejo usando reglas con condiciones más complejas que consisten en varias características: Cobertura secuencial.

4.5.2 Cobertura secuencial

La cobertura secuencial es un procedimiento general que aprende repetidamente una sola regla para crear una lista de decisiones (o conjunto) que cubre todo el conjunto de datos regla por regla. Muchos algoritmos de aprendizaje de reglas son variantes del algoritmo de cobertura secuencial. Este capítulo presenta la receta principal y utiliza RIPPER, una variante del algoritmo de cobertura secuencial para los ejemplos.

La idea es simple: Primero, encuentra una buena regla que se aplique a algunos de los puntos de datos. Eliminatodos los puntos de datos cubiertos por la regla. Se cubre un punto de datos cuando se aplican las condiciones, independientemente de si los puntos se clasifican correctamente o no. Repite el aprendizaje de reglas y la eliminación de los puntos cubiertos con los puntos restantes hasta que no queden más puntos o se cumpla otra condición de detención. El resultado es una lista de decisiones. Este enfoque de aprendizaje de reglas repetido y eliminación de puntos de datos cubiertos se denomina “dividir y conquistar”.

Supongamos que ya tenemos un algoritmo que puede crear una sola regla que cubra parte de los datos. El algoritmo de cobertura secuencial para dos clases (una positiva, una negativa) funciona así:

• Comienza con una lista vacía de reglas (rlist).
• Aprende una regla r.
• Si bien la lista de reglas está por debajo de cierto umbral de calidad (o los ejemplos positivos aún no están cubiertos):
  • Agrega la regla r a rlist.
  • Elimina todos los puntos de datos cubiertos por la regla r.
  • Aprende otra regla sobre los datos restantes.
• Devuelve la lista de decisiones.

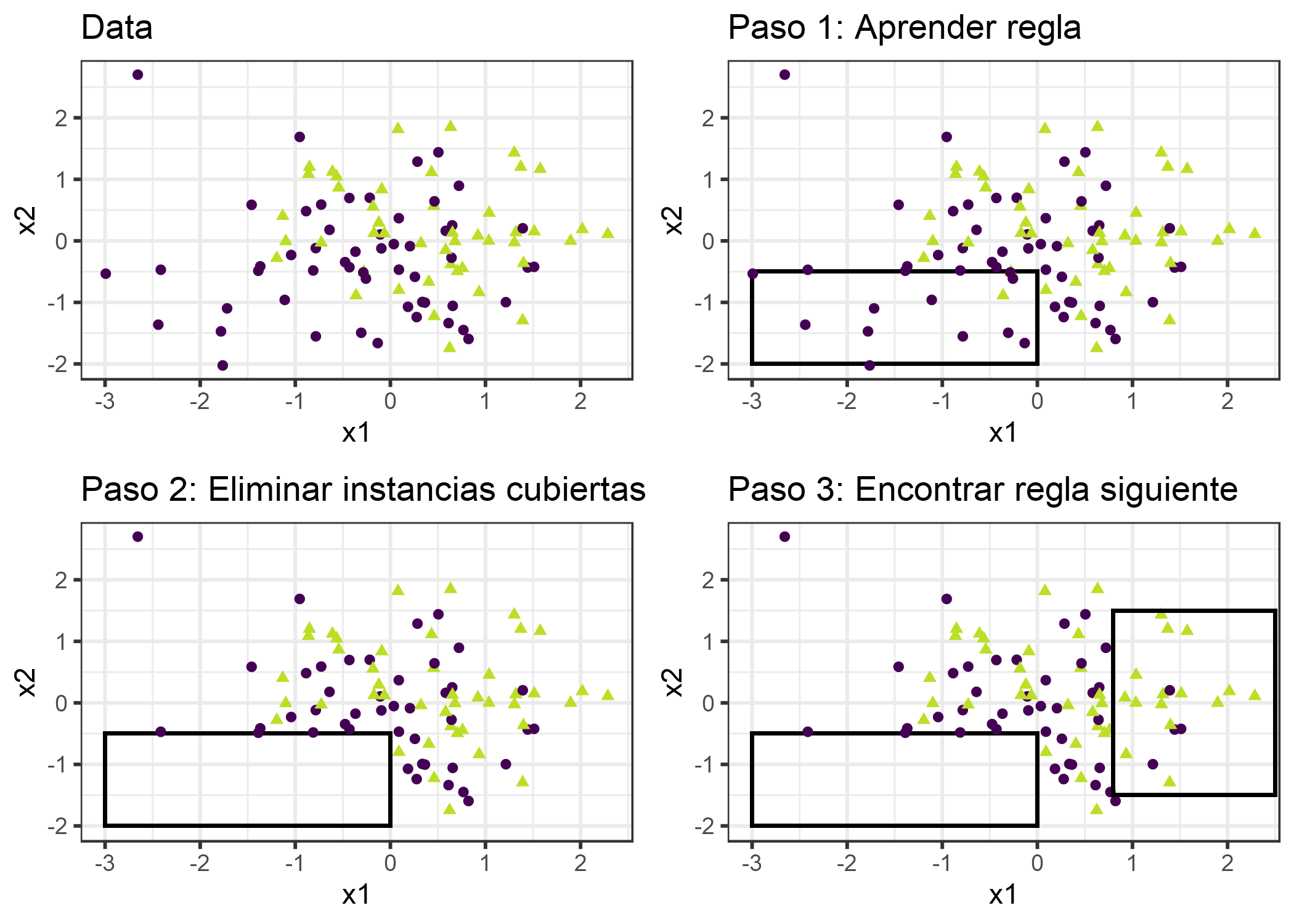
FIGURA 4.18: El algoritmo de cobertura funciona cubriendo secuencialmente el espacio de características con reglas individuales y eliminando los puntos de datos que ya están cubiertos por esas reglas. Para fines de visualización, las características x1 y x2 son continuas, pero la mayoría de los algoritmos de aprendizaje de reglas requieren caracteristicas categóricas.

Por ejemplo: Tenemos una tarea y un conjunto de datos para predecir los valores de las casas por tamaño, ubicación y si se permiten mascotas. Aprendemos la primera regla, que resulta ser: Si tamaño = grande y ubicación = buena, entonces valor = alto. Luego eliminamos todas las casas grandes en buenas ubicaciones del conjunto de datos. Con los datos restantes aprendemos la siguiente regla. Quizás: si ubicación = buena, entonces valor = medio. Ten en cuenta que esta regla se aprende en datos sin grandes casas en buenas ubicaciones, dejando solo casas medianas y pequeñas en buenas ubicaciones.

Para configuraciones de varias clases, el enfoque debe modificarse. Primero, las clases se ordenan aumentando la prevalencia. El algoritmo de cobertura secuencial comienza con la clase menos común, aprende una regla para ello, elimina todas las instancias cubiertas, luego pasa a la segunda clase menos común y así sucesivamente. La clase actual siempre se trata como la clase positiva y todas las clases con una prevalencia más alta se combinan en la clase negativa. La última clase es la regla predeterminada. Esto también se conoce como estrategia de uno contra todos en la clasificación.

¿Cómo aprendemos una sola regla? El algoritmo OneR sería inútil aquí, ya que siempre cubriría todo el espacio de características. Pero hay muchas otras posibilidades. Una posibilidad es aprender una sola regla de un árbol de decisión con ‘beam search’ (búsqueda de haz):

• Aprende un árbol de decisión (con CART u otro algoritmo de aprendizaje de árbol).
• Comienza en el nodo raíz y selecciona recursivamente el nodo más puro (por ejemplo, con la tasa de clasificación errónea más baja).
• La clase mayoritaria del nodo terminal se usa como la predicción de la regla; la ruta que conduce a ese nodo se usa como condición de regla.

La siguiente figura ilustra la búsqueda del haz en un árbol:

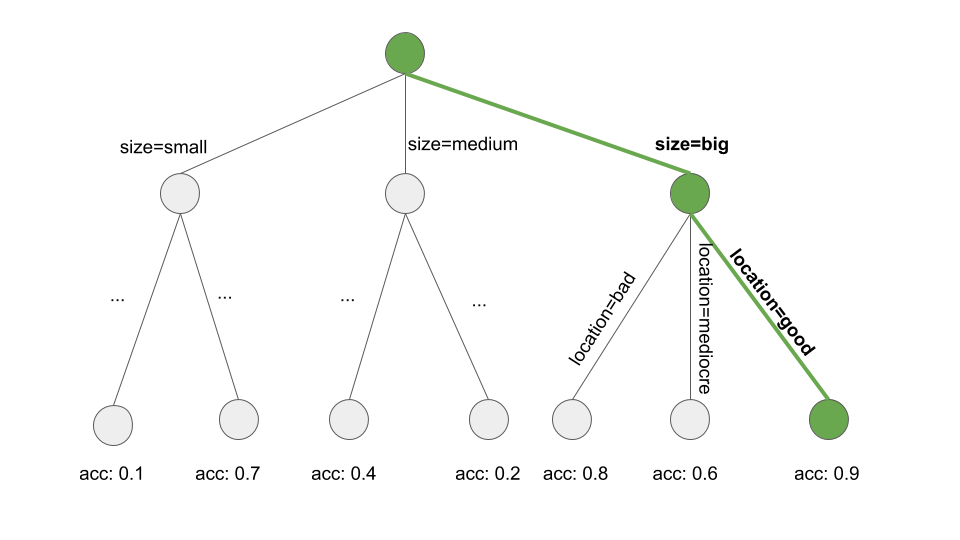
FIGURA 4.19: Aprender una regla buscando una ruta a través de un árbol de decisión. Comienza en el nodo raíz, con avidez e iteración sigue la ruta que produce localmente el subconjunto más puro (por ejemplo, la precisión más alta) y agrega todos los valores divididos a la condición de la regla. Termina con: Si ubicación = buena y tamaño = grande, entonces valor = alto.

Aprender una sola regla es un problema de búsqueda, donde el espacio de búsqueda es el espacio de todas las reglas posibles. El objetivo de la búsqueda es encontrar la mejor regla de acuerdo con algunos criterios. Existen muchas estrategias de búsqueda diferentes: hill-climbing, beam search, exhaustive search, búsqueda de primer orden, búsqueda ordenada, búsqueda estocástica, búsqueda de arriba hacia abajo, búsqueda de abajo hacia arriba, …

RIPPER (poda incremental repetida para producir reducción de errores) por Cohen (1995)¹⁹ es una variante del algoritmo de cobertura secuencial. RIPPER es un poco más sofisticado y utiliza una fase de posprocesamiento (poda de reglas) para optimizar la lista de decisiones (o conjunto). RIPPER puede ejecutarse en modo ordenado o no ordenado y generar una lista de decisiones o un conjunto de decisiones.

Ejemplos

Usaremos RIPPER para los ejemplos.

El algoritmo RIPPER no encuentra ninguna regla en la tarea de clasificación para cáncer cervical.

Cuando usamos RIPPER en la tarea de regresión para predecir recuento de bicicletas se encuentran algunas reglas. Dado que RIPPER solo funciona para la clasificación, el conteo de bicicletas debe convertirse en un resultado categórico. Lo logré cortando los recuentos de bicicletas en los cuartiles. Por ejemplo (4548, 5956) es el intervalo que cubre el recuento previsto de bicicletas entre 4548 y 5956. La siguiente tabla muestra la lista de decisiones de las reglas aprendidas.

rules
(days_since_2011 >= 438) and (temp >= 17) and (temp <= 27) and (hum <= 67) => cnt=(5956,8714]
(days_since_2011 >= 443) and (temp >= 12) and (weathersit = GOOD) and (hum >= 59) => cnt=(5956,8714]
(days_since_2011 >= 441) and (windspeed <= 10) and (temp >= 13) => cnt=(5956,8714]
(temp >= 12) and (hum <= 68) and (days_since_2011 >= 551) => cnt=(5956,8714]
(days_since_2011 >= 100) and (days_since_2011 <= 434) and (hum <= 72) and (workingday = WORKING DAY) => cnt=(3152,4548]
(days_since_2011 >= 106) and (days_since_2011 <= 323) => cnt=(3152,4548]
=> cnt=[22,3152]

La interpretación es simple: Si se aplican las condiciones, predecimos el intervalo en el lado derecho para el número de bicicletas. La última regla es la regla predeterminada que se aplica cuando ninguna de las otras reglas se aplica a una instancia. Para predecir una nueva instancia, comienza en la parte superior de la lista y verifica si se aplica una regla. Cuando una condición coincide, el lado derecho de la regla es la predicción para esta instancia. La regla predeterminada asegura que siempre haya una predicción.

4.5.3 Listas de reglas bayesianas

En esta sección, se mostrará otro enfoque para aprender una lista de decisiones, que sigue esta receta aproximada:

1. Pre-mina los patrones frecuentes de los datos que pueden usarse como condiciones para las reglas de decisión.
2. Aprende una lista de decisiones de una selección de las reglas previamente minadas.

Un enfoque específico que utiliza esta receta se llama Listas de Reglas Bayesianas (Letham et. Al., 2015)²⁰ o BRL para abreviar. BRL utiliza estadísticas bayesianas para aprender listas de decisiones de patrones frecuentes que se extraen previamente con el algoritmo FP-tree (Borgelt 2005)²¹

Pero comencemos lentamente con el primer paso de BRL.

Pre-minería de patrones frecuentes

Un patrón frecuente es la aparición frecuente y conjunta de valores de características. Como un paso de preprocesamiento para el algoritmo BRL, utilizamos las características (no necesitamos el resultado objetivo en este paso) y extraemos patrones que ocurren con frecuencia de ellos. Un patrón puede ser un valor de entidad único como peso = medio o una combinación de valores de entidad como peso = medio Y ubicación = mala.

La frecuencia de un patrón se mide con su soporte en el conjunto de datos:

\[Support(x_j=A)=\frac{1}n{}\sum_{i=1}^nI(x^{(i)}_{j}=A)\]

donde A es el valor de la característica, n el número de puntos de datos en el conjunto de datos e I la función de identidad que devuelve 1 si la función \(x_j\) de la instancia i tiene el nivel A, de lo contrario 0. En un conjunto de datos de valores de casas, si el 20% de las casas no tiene balcón y el 80% tiene uno o más, entonces el soporte para el patrón balcón = 0 es del 20%. El soporte también se puede medir para combinaciones de valores de características, por ejemplo para balcón = 0 Y mascotas = permitido.

Existen muchos algoritmos para encontrar patrones tan frecuentes, por ejemplo, Apriori o FP-Growth. Lo que usa no importa mucho, solo la velocidad a la que se encuentran los patrones es diferente, pero los patrones resultantes son siempre los mismos.

Daré una idea aproximada de cómo funciona el algoritmo Apriori para encontrar patrones frecuentes. En realidad, el algoritmo Apriori consta de dos partes, donde la primera parte encuentra patrones frecuentes y la segunda parte crea reglas de asociación a partir de ellos. Para el algoritmo BRL, solo estamos interesados en los patrones frecuentes que se generan en la primera parte de Apriori.

En el primer paso, el algoritmo Apriori comienza con todos los valores de características que tienen un soporte mayor que el soporte mínimo definido por el usuario. Si el usuario dice que el soporte mínimo debe ser del 10% y solo el 5% de las casas tienen peso = grande, eliminaríamos ese valor de la característica y mantendríamos solo peso = medio y peso = chico como patrones. Esto no significa que las casas se eliminen de los datos, solo significa que peso = grande no se devuelve como un patrón frecuente. Basado en patrones frecuentes con un solo valor de característica, el algoritmo Apriori intenta iterativamente encontrar combinaciones de valores de característica de orden cada vez más alto. Los patrones se construyen combinando declaraciones característica = valor con un Y lógico, por ejemplo peso = medio Y ubicación = mala. Se eliminan los patrones generados con un soporte por debajo del soporte mínimo. Al final tenemos todos los patrones frecuentes. Cualquier subconjunto de un patrón frecuente es frecuente nuevamente, lo que se llama la propiedad Apriori. Tiene sentido intuitivamente: Al eliminar una condición de un patrón, el patrón reducido solo puede cubrir más o la misma cantidad de puntos de datos, pero no menos. Por ejemplo, si el 20% de las casas son peso = medio Y ubicación = buena, entonces el soporte de las casas que son solo peso = medio es 20% o más. La propiedad Apriori se usa para reducir el número de patrones que se inspeccionarán. Solo en el caso de patrones frecuentes tenemos que verificar patrones de orden superior.

Ahora hemos terminado con las condiciones previas a la minería para las Listas de Reglas Bayesianas. Pero antes de pasar al segundo paso de BRL, me gustaría insinuar otra forma para el aprendizaje de reglas basado en patrones pre-minados. Otros enfoques sugieren incluir el resultado de interés en el proceso frecuente de minería de patrones y también ejecutar la segunda parte del algoritmo Apriori que construye las reglas SI-ENTONCES. Dado que el algoritmo no está supervisado, la parte ENTONCES también contiene valores de características que no nos interesan. Pero podemos filtrar por reglas que solo tienen el resultado de interés en la parte ENTONCES. Estas reglas ya forman un conjunto de decisiones, pero también sería posible organizar, podar, eliminar o recombinar las reglas.

4.5.4 Ventajas

Esta sección discute los beneficios de las reglas SI-ENTONCES en general.

Las reglas SI-ENTONCES son fáciles de interpretar. Son probablemente el más interpretable de los modelos interpretables. Esta declaración solo se aplica si el número de reglas es pequeño, las condiciones de las reglas son cortas (máximo 3, diría yo) y si las reglas están organizadas en una lista de decisiones o en un conjunto de decisiones que no se superponen.

Las reglas de decisión pueden ser tan expresivas como los árboles de decisión, mientras que son más compactas. Los árboles de decisión a menudo también sufren de subárboles replicados, es decir, cuando las divisiones en un nodo secundario izquierdo y derecho tienen la misma estructura.

La predicción con las reglas SI-ENTONCES es rápida, ya que solo se necesitan verificar unas pocas declaraciones binarias para determinar qué reglas se aplican.

Las reglas de decisión son robustas contra las transformaciones monótonas de las características de entrada, sólo cambiará el umbral de las condiciones. También son robustas frente a los valores atípicos, ya que solo importa si una condición se aplica o no.

Las reglas SI-ENTONCES generalmente generan modelos dispersos, lo que significa que no se incluyen muchas características. Seleccionan solo las características relevantes para el modelo. Por ejemplo, un modelo lineal asigna un peso a cada característica de entrada de forma predeterminada. Las características que son irrelevantes pueden simplemente ser ignoradas por las reglas SI-ENTONCES.

Reglas simples como las de OneR pueden usarse como línea de base para algoritmos más complejos.

4.5.5 Desventajas

Esta sección trata las desventajas de las reglas SI-ENTONCES en general.

La investigación y la literatura para las reglas SI-ENTONCES se enfoca en la clasificación y casi descuida completamente la regresión. Si bien siempre puede dividir un objetivo continuo en intervalos y convertirlo en un problema de clasificación, siempre pierde información. En general, los enfoques son más atractivos si pueden usarse tanto para la regresión como para la clasificación.

A menudo, las características también tienen que ser categóricas. Eso significa que las características numéricas deben clasificarse si desea usarlas. Hay muchas formas de cortar una característica continua en intervalos, pero esto no es trivial y viene con muchas preguntas sin respuestas claras. ¿En cuántos intervalos debe dividirse la función? ¿Cuál es el criterio de división: longitudes de intervalo fijas, cuantiles u otra cosa? La categorización de características continuas es un problema no trivial que a menudo se descuida y las personas simplemente usan el siguiente mejor método (como lo hice en los ejemplos).

Muchos de los algoritmos de aprendizaje de reglas más antiguos son propensos al sobreajuste. Todos los algoritmos presentados aquí tienen al menos algunas garantías para evitar el sobreajuste: OneR es limitado porque solo puede usar una característica (solo problemático si la característica tiene demasiados niveles o si hay muchas características, lo que equivale al problema de prueba múltiple), RIPPER hace podas y las listas de reglas bayesianas imponen una distribución previa de la lista de decisión.

Las reglas de decisión son malas al describir relaciones lineales entre características y resultados. Ese es un problema que comparten con los árboles de decisión. Los árboles de decisión y las reglas solo pueden producir funciones de predicción escalonadas, donde los cambios en la predicción siempre son pasos discretos y nunca curvas suaves. Esto está relacionado con el problema de que las entradas tienen que ser categóricas. En los árboles de decisión, se clasifican implícitamente dividiéndolos.

4.5.6 Software y alternativas

OneR se implementa en el paquete R OneR, que se utilizó para los ejemplos en este libro. OneR también se implementa en la librería de aprendizaje automático Weka y, como tal, disponible en Java, R y Python. RIPPER también se implementa en Weka. Para los ejemplos, utilicé la implementación R de JRIP en el paquete RWeka. SBRL está disponible como paquete R (que utilicé para los ejemplos), en Python o como implementación C.

Ni siquiera intentaré enumerar todas las alternativas para aprender conjuntos de reglas de decisión y listas, sino que señalaré algunos trabajos de resumen. Recomiendo el libro “Fundamentos del aprendizaje de reglas” de Fuernkranz et. al (2012)²². Es un trabajo extenso sobre reglas de aprendizaje, para aquellos que desean profundizar en el tema. Proporciona un marco holístico para pensar sobre las reglas de aprendizaje y presenta muchos algoritmos de aprendizaje de reglas. También recomiendo revisar los Estudiantes de reglas de Weka, que implementan RIPPER, M5Rules, OneR, PART y muchos más. Las reglas SI-ENTONCES pueden usarse en modelos lineales como se describe en este libro en el capítulo sobre el algoritmo RuleFit.

---

18. Holte, Robert C. “Very simple classification rules perform well on most commonly used datasets.” Machine learning 11.1 (1993): 63-90.↩

19. Cohen, William W. “Fast effective rule induction.” Machine Learning Proceedings (1995). 115-123.↩

20. Letham, Benjamin, et al. “Interpretable classifiers using rules and Bayesian analysis: Building a better stroke prediction model.” The Annals of Applied Statistics 9.3 (2015): 1350-1371.↩

21. Borgelt, C. “An implementation of the FP-growth algorithm.” Proceedings of the 1st International Workshop on Open Source Data Mining Frequent Pattern Mining Implementations - OSDM ’05, 1–5. http://doi.org/10.1145/1133905.1133907 (2005).↩

22. Fürnkranz, Johannes, Dragan Gamberger, and Nada Lavrač. “Foundations of rule learning.” Springer Science & Business Media, (2012).↩