5.5 Importancia de la característica de permutación

La importancia de la característica de permutación mide el aumento en el error de predicción del modelo después de permutar los valores de la característica, lo que rompe la relación entre la característica y el resultado real.

5.5.1 Teoría

El concepto es realmente sencillo: Medimos la importancia de una característica calculando el aumento en el error de predicción del modelo después de permutar la característica. Una característica es “importante” si cambiar sus valores aumenta el error del modelo, porque en este caso el modelo se basó en la característica para la predicción. Una característica es “no importante” si cambiar sus valores deja el error del modelo sin cambios, porque en este caso el modelo ignoró la característica para la predicción. Breiman (2001)³⁴ introdujo la medida de importancia de la característica de permutación para random forest. En base a esta idea, Fisher, Rudin y Dominici (2018)³⁵ propusieron una versión independiente del modelo de la importancia de la característica y la llamaron dependencia del modelo. También introdujeron ideas más avanzadas sobre la importancia de las características, por ejemplo, una versión (específica del modelo) que tiene en cuenta que muchos modelos de predicción pueden predecir bien los datos. Vale la pena leer su artículo.

El algoritmo de importancia de la característica de permutación basado en Fisher, Rudin y Dominici (2018):

Entrada: Modelo entrenado f, matriz de características X, vector objetivo y, medida de error L(y,f).

1. Estima el error del modelo original e^orig = L(y, f(X)) (por ejemplo, error cuadrático medio)
2. Para cada característica j = 1, …, p:
   • Genera la matriz de características X^perm permutando la característica j en los datos X. Esto rompe la asociación entre la característica j y el resultado verdadero y.
   • Estima el error e^perm = L(Y,f(X^perm)) en función de las predicciones de los datos permutados.
   • Calcula la importancia de la característica de permutación FI^j = e^perm/e^orig. Alternativamente, se puede usar la diferencia: FI^j = e^perm-e^orig
3. Ordena las características por FI descendente.

Fisher, Rudin y Dominici (2018) sugieren en su artículo dividir el conjunto de datos a la mitad e intercambiar los valores de la característica j de las dos mitades en lugar de permutar la característica j. Esto es exactamente lo mismo que permutar la función j, si lo piensas. Si deseas una estimación más precisa, puedes estimar el error de permutar la característica j emparejando cada instancia con el valor de la característica j de cada otra instancia (excepto consigo misma). Esto te proporciona un conjunto de datos de tamaño n(n-1) para estimar el error de permutación, y requiere una gran cantidad de tiempo de cálculo. Solo puedo recomendar el uso del método n(n-1) si realmente quieres obtener estimaciones extremadamente precisas.

5.5.2 ¿Debo calcular la importancia de los datos de entrenamiento o prueba?

tl;dr: no tengo una respuesta definitiva.

La respuesta a la pregunta sobre los datos de entrenamiento o prueba toca la pregunta fundamental de qué importancia tiene la característica. La mejor manera de comprender la diferencia entre la importancia de la característica basada en el entrenamiento frente a los datos de la prueba es un ejemplo “extremo”. Entrené a una SVM para predecir un resultado objetivo aleatorio continuo con 50 características aleatorias (200 instancias). Por “aleatorio” quiero decir que el resultado objetivo es independiente de las 50 características. Esto es como predecir la temperatura de mañana dados los últimos números de lotería. Si el modelo “aprende” alguna relación, entonces se sobreajusta. Y, de hecho, el SVM superó los datos de entrenamiento. El error absoluto medio (corto: MAE) para los datos de entrenamiento es 0.29 y para los datos de prueba 0.82, que también es el error del mejor modelo posible que siempre predice el resultado medio de 0 (MAE de 0.78). En otras palabras, el modelo SVM es basura. ¿Qué valores para la importancia de la característica esperarías para las 50 características de este SVM sobreajustado? ¿Cero porque ninguna de las características contribuye a mejorar el rendimiento en datos de prueba no vistos? ¿O deberían las importancias reflejar cuánto depende el modelo de cada una de las características, independientemente de si las relaciones aprendidas se generalizan a datos no vistos? Echemos un vistazo a cómo difieren las distribuciones de las características importantes para los datos de entrenamiento y prueba.

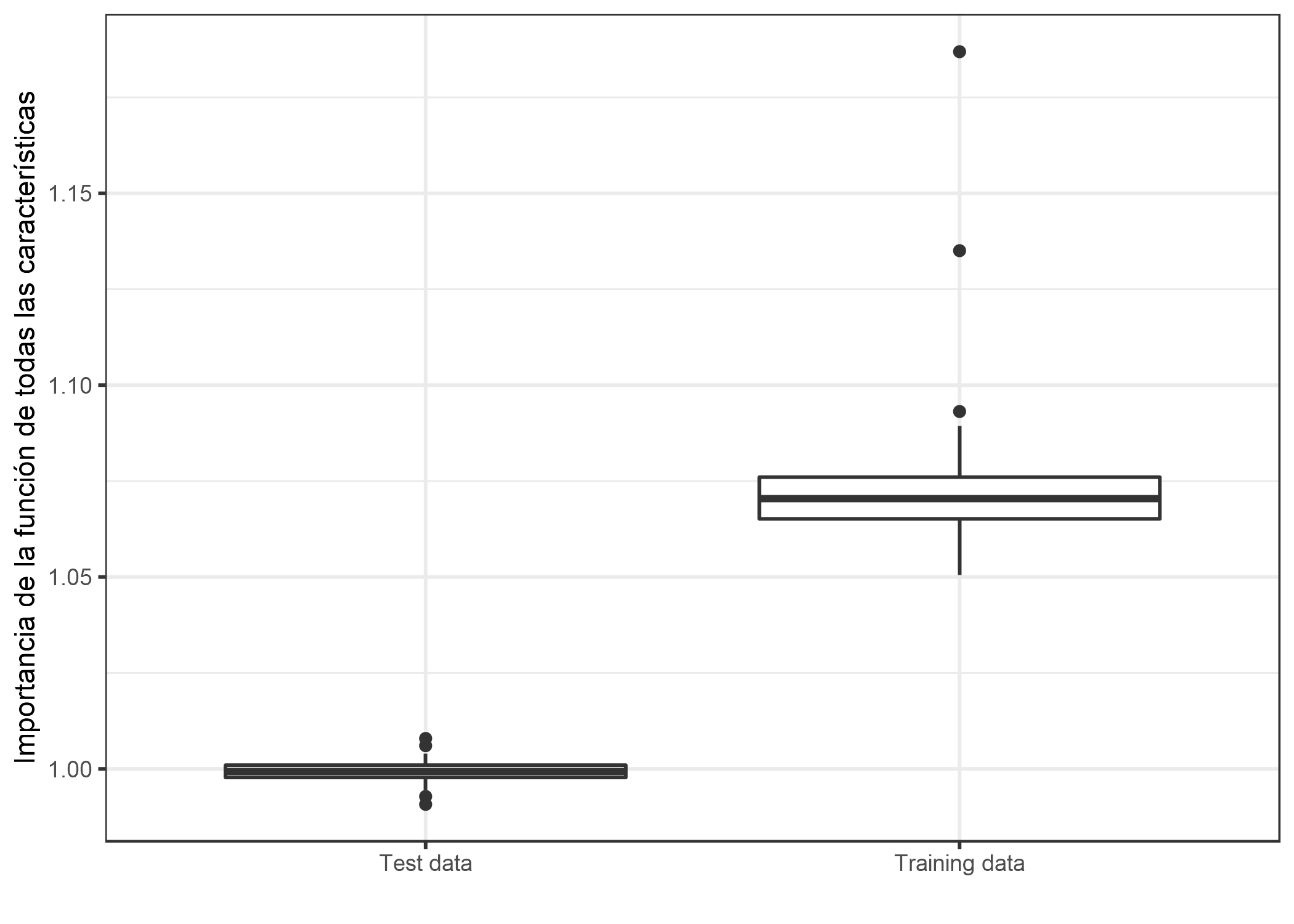
FIGURA 5.27: Distribuciones de valores de importancia de características por tipo de datos. Un SVM fue entrenado en un conjunto de datos de regresión con 50 características aleatorias y 200 instancias. en los datos de entrenamiento muestra muchas características importantes. Calculadas en datos de prueba no vistos, las importancias de las características son cercanas a una proporción de uno (= sin importancia).

No me queda claro cuál de los dos resultados es más deseable. Así que intentaré presentar un caso para ambas versiones y dejarte que decidas.

El caso de los datos de prueba

Este es un caso simple: Las estimaciones de error del modelo basadas en datos de entrenamiento son basura -> la importancia de la característica depende de las estimaciones de error del modelo -> la importancia de la característica basada en datos de entrenamiento es basura. Es una de las primeras cosas que aprendes en el aprendizaje automático: Si mides el error del modelo (o el rendimiento) en los mismos datos en los que se formó el modelo, la medición suele ser demasiado optimista, lo que significa que el modelo parece funcionar mucho mejor de lo que realmente lo hace. Y dado que la importancia de la característica de permutación se basa en mediciones del error del modelo, debemos usar datos de prueba no vistos. La importancia de la característica basada en los datos de entrenamiento nos hace creer erróneamente que las características son importantes para las predicciones, cuando en realidad el modelo simplemente estaba sobreajustado y las características no eran importantes en absoluto.

El caso de los datos de entrenamiento

Los argumentos para usar datos de entrenamiento son algo más difíciles de formular, pero en mi humilde opinión son tan convincentes como los argumentos para usar datos de prueba. Echamos otro vistazo a nuestra basura SVM. Según los datos de entrenamiento, la característica más importante era X42. Veamos un diagrama de dependencia parcial de la característica X42. El gráfico de dependencia parcial muestra cómo cambia la salida del modelo en función de los cambios de la característica y no se basa en el error de generalización. No importa si el PDP se calcula con datos de entrenamiento o prueba.

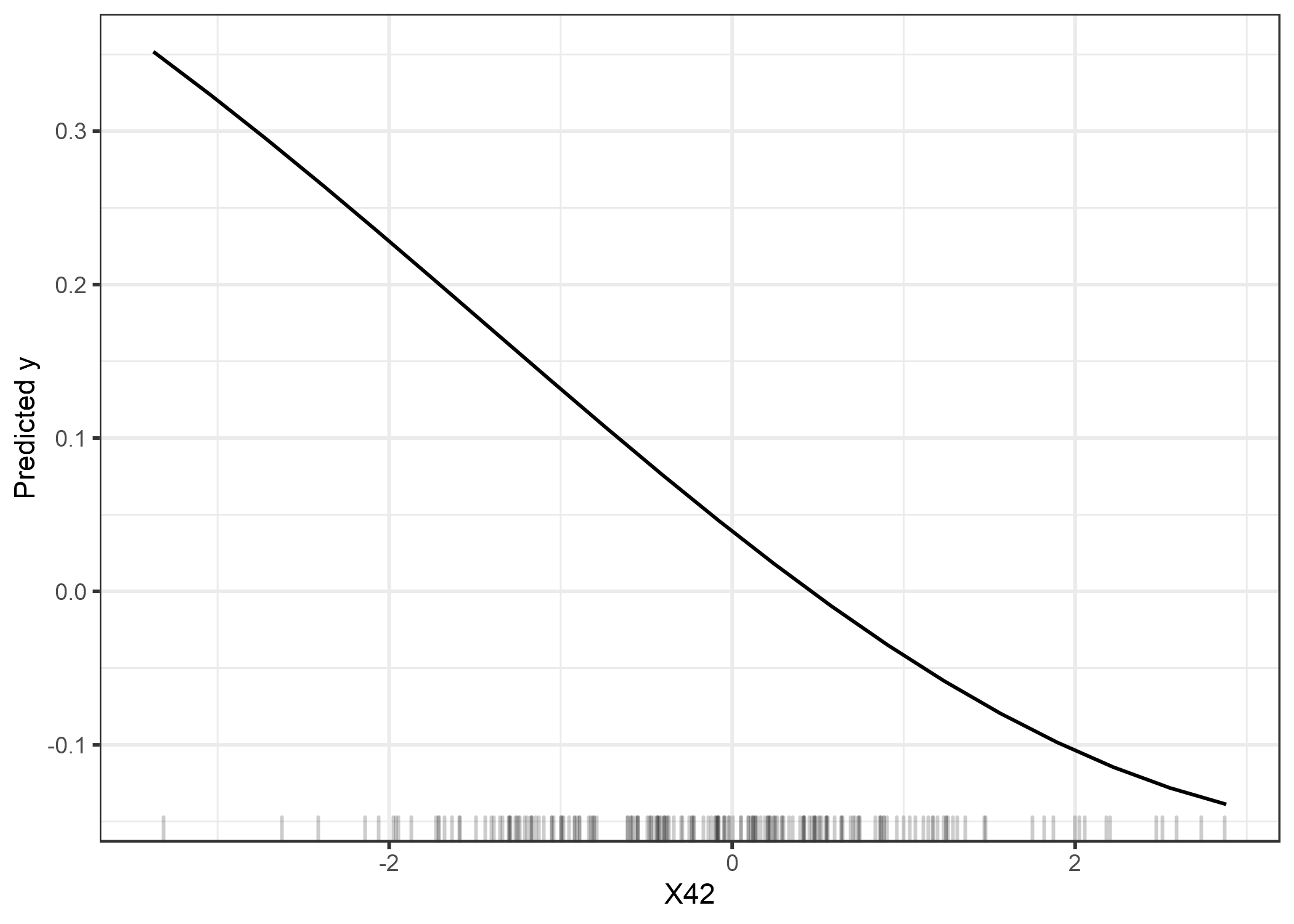
FIGURA 5.28: PDP de la característicaX42, que es la característica más importante según la importancia de la característica en función de los datos de entrenamiento. El gráfico muestra cómo el SVM depende de esto función para hacer predicciones

La gráfica muestra claramente que el SVM ha aprendido a confiar en la función X42 para sus predicciones, pero de acuerdo con la importancia de la función basada en los datos de prueba (1), no es importante. Según los datos de entrenamiento, la importancia es 1.19, lo que refleja que el modelo ha aprendido a usar esta función. La importancia de la característica basada en los datos de entrenamiento nos dice qué características son importantes para el modelo en el sentido de que depende de ellas para hacer predicciones.

Como parte del caso para usar datos de entrenamiento, me gustaría presentar un argumento en contra de los datos de prueba. En la práctica, deseas utilizar todos tus datos para entrenar tu modelo para obtener el mejor modelo posible al final. Esto significa que no quedan datos de prueba no utilizados para calcular la importancia de la característica. Tienes el mismo problema cuando deseas estimar el error de generalización de su modelo. Si usaras la validación cruzada (anidada) para la estimación de la importancia de la característica, tendrías el problema de que la importancia de la característica no se calcula en el modelo final con todos los datos, sino en modelos con subconjuntos de datos que podrían comportarse de manera diferente.

Al final, debes decidir si deseas saber cuánto depende el modelo de cada característica para hacer predicciones (-> datos de entrenamiento) o cuánto contribuye la característica al rendimiento del modelo en datos no vistos (-> datos de prueba) Que yo sepa, no hay ninguna investigación que aborde la cuestión de los datos de entrenamiento versus los datos de las pruebas. Se requerirá un examen más exhaustivo que mi ejemplo “basura-SVM”. Necesitamos más investigación y más experiencia con estas herramientas para obtener una mejor comprensión.

A continuación, veremos algunos ejemplos. Basé el cálculo de importancia en los datos de entrenamiento, porque tenía que elegir uno y usar los datos de entrenamiento necesitaba algunas líneas menos código.

5.5.3 Ejemplo e interpretación

Muestro ejemplos de clasificación y regresión.

Cáncer de cuello uterino (clasificación)

Ajustamos un random forest para predecir cáncer cervical. Medimos el aumento de error en 1-AUC (1 menos el área bajo la curva ROC). Las características asociadas con un aumento del error del modelo por un factor de 1 (= sin cambio) no fueron importantes para predecir el cáncer cervical.

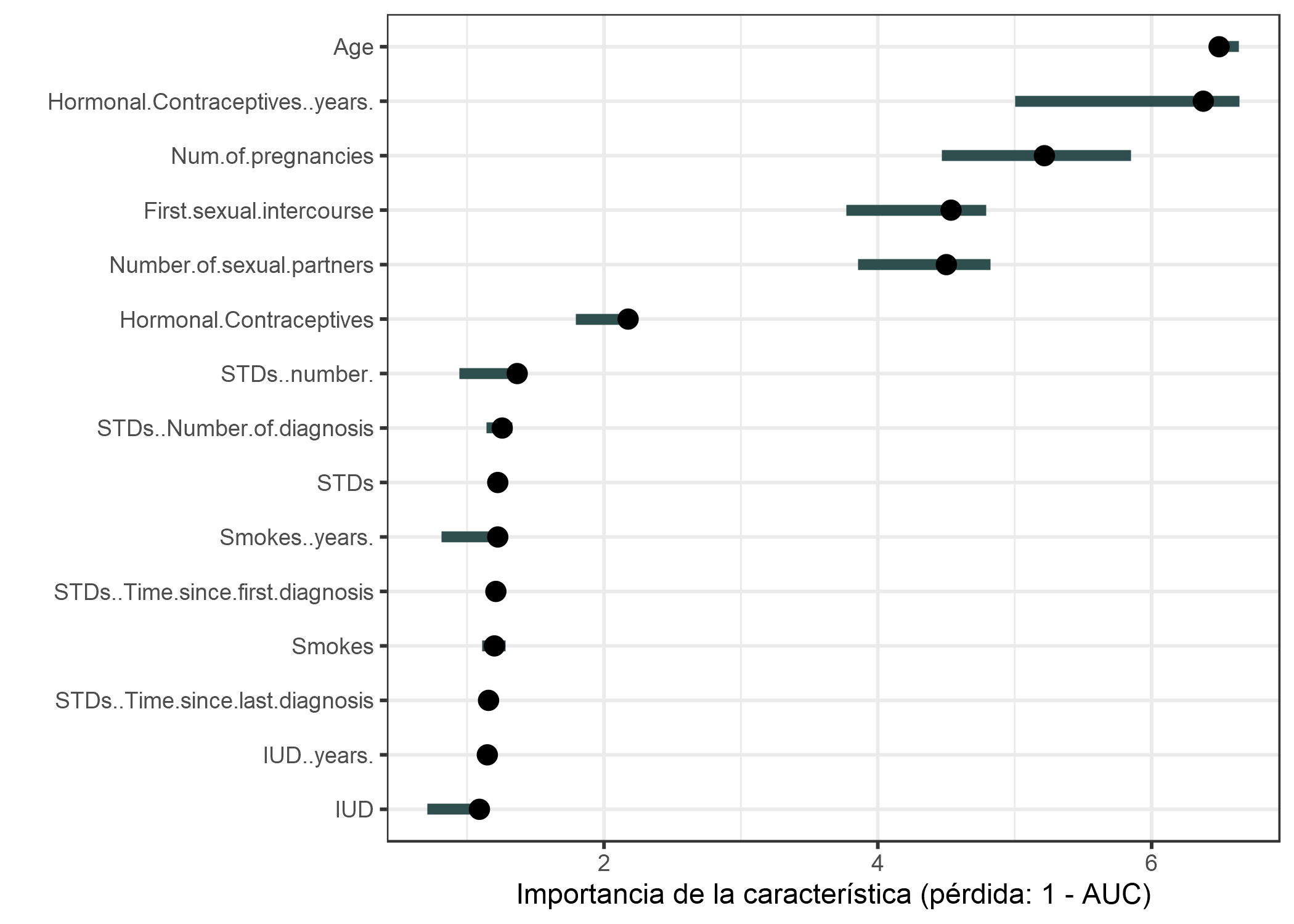
FIGURA 5.29: La importancia de cada una de las características prediciendo cáncer cervical con un random forest. La más importante fue Age. Permutar Age resulta en un incremento de 1-AUC a razón de 6.49

La característica con mayor importancia fue Age asociada con un aumento de error de 6.49 después de la permutación.

Bicicleta compartida (regresión)

Ajustamos un modelo de SVM para predecir el número de bicicletas alquiladas, dadas las condiciones climáticas y la información del calendario. Como medida de error usamos el error absoluto medio.

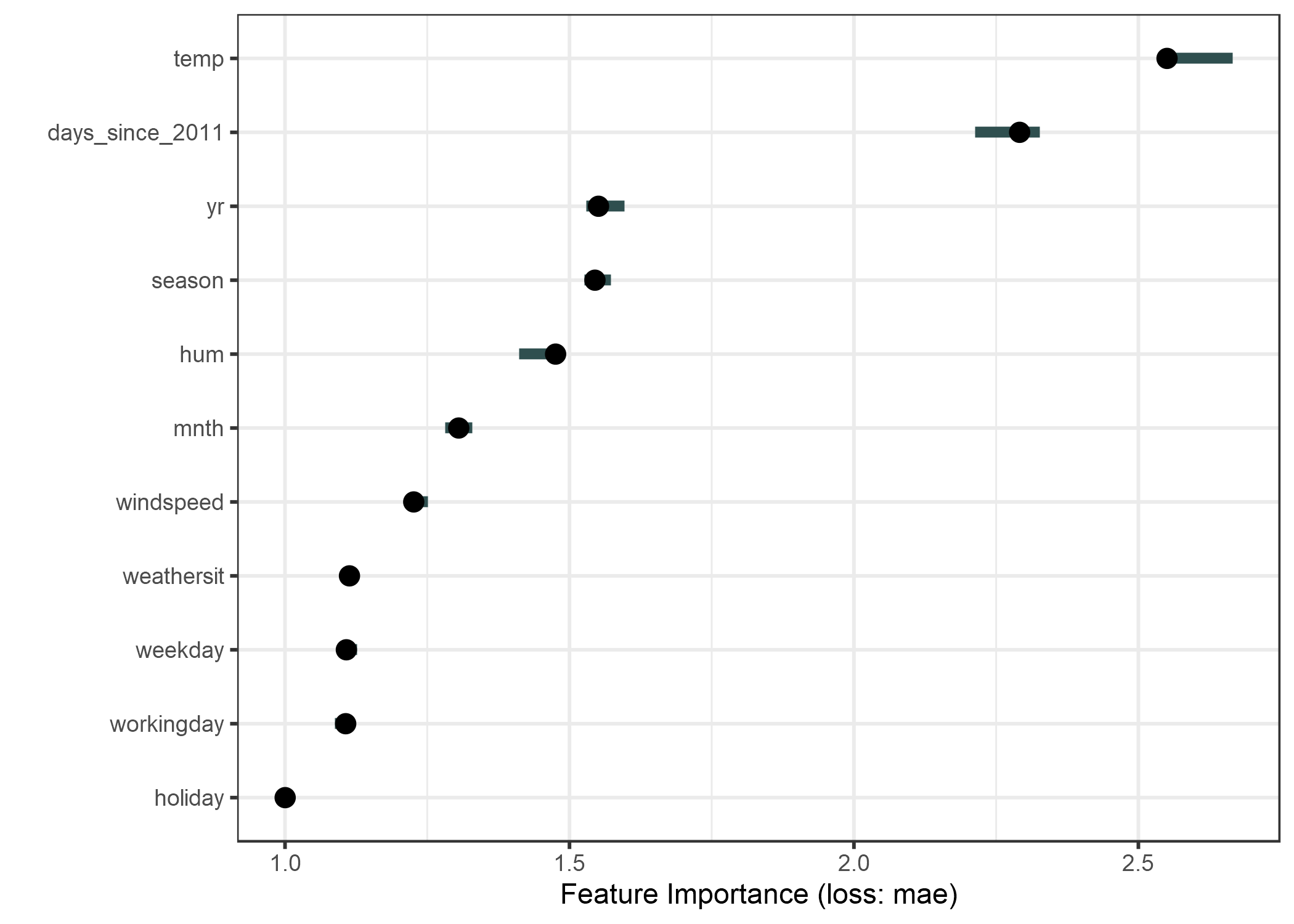
FIGURA 5.30: La importancia para cada una de las características en la predicción de la bicicleta cuenta con una máquina de vectores de soporte. La característica más importante fue temp, la menos importante fue holiday.

5.5.4 Ventajas

Buena interpretación: la importancia de la característica es el aumento en el error del modelo cuando se destruye la información de la característica.

La importancia de la característica proporciona una visión global altamente comprimida sobre el comportamiento del modelo.

Un aspecto positivo del uso de la relación de error en lugar de la diferencia de error es que las mediciones de importancia de la característica son comparables entre diferentes problemas.

La medida de importancia automáticamente tiene en cuenta todas las interacciones con otras características. Al permutar la función, también destruye los efectos de interacción con otras características. Esto significa que la importancia de la característica de permutación tiene en cuenta tanto el efecto de la característica principal como los efectos de interacción en el rendimiento del modelo. Esto también es una desventaja porque la importancia de la interacción entre dos características está incluida en las mediciones de importancia de ambas características. Esto significa que las características importantes no se suman a la caída total en el rendimiento, pero la suma es mayor. Solo si no hay interacción entre las características, como en un modelo lineal, las importancias se suman aproximadamente.

La importancia de la característica de permutación no requiere volver a entrenar el modelo. Algunos otros métodos sugieren eliminar una función, volver a entrenar el modelo y luego comparar el error del modelo. Dado que el reciclaje de un modelo de aprendizaje automático puede llevar mucho tiempo, “solo” permutar una función puede ahorrar mucho tiempo. Los métodos de importancia que vuelven a entrenar el modelo con un subconjunto de características parecen intuitivos a primera vista, pero el modelo con los datos reducidos no tiene sentido para la importancia de la característica. Estamos interesados en la importancia de las características de un modelo fijo. Volver a entrenar con un conjunto de datos reducido crea un modelo diferente al que nos interesa. Supón que entrenas un modelo lineal disperso (con lasso) con un número fijo de características con un peso distinto de cero. El conjunto de datos tiene 100 características, estableces el número de pesos distintos de cero a 5. Analizas la importancia de una de las características que tienen un peso distinto de cero. Eliminas la función y vuelves a entrenar el modelo. El rendimiento del modelo sigue siendo el mismo porque otra característica igualmente buena obtiene un peso distinto de cero y tu conclusión sería que la característica no era importante. Otro ejemplo: El modelo es un árbol de decisión y analizamos la importancia de la función elegida como la primera división. Elimina la función y vuelves a entrenar el modelo. Dado que se elige otra característica como la primera división, todo el árbol puede ser muy diferente, lo que significa que comparamos las tasas de error de árboles (potencialmente) completamente diferentes para decidir qué tan importante es esa característica para uno de los árboles.

5.5.5 Desventajas

No está muy claro si debe utilizar los datos de entrenamiento o prueba para calcular la importancia de la función.

La importancia de la característica de permutación está vinculada al error del modelo. Esto no es inherentemente malo, pero en algunos casos no es lo que necesitas. En algunos casos, es posible que prefieras saber cuánto varía la salida del modelo para una característica sin tener en cuenta lo que significa para el rendimiento. Por ejemplo, deseas averiguar qué tan robusta es la salida de tu modelo cuando alguien manipula las características. En este caso, no le interesaría cuánto disminuye el rendimiento del modelo cuando se permuta una característica, sino cuánto explica cada característica la variación de salida del modelo. La varianza del modelo (explicada por las características) y la importancia de la característica se correlacionan fuertemente cuando el modelo se generaliza bien (es decir, no se sobreajusta).

Necesitas acceso al verdadero resultado. Si alguien solo te proporciona el modelo y los datos no etiquetados, pero no el resultado real, no puedes calcular la importancia de la característica de permutación.

La importancia de la característica de permutación depende de barajar la característica, lo que agrega aleatoriedad a la medición. Cuando se repite la permutación, los resultados pueden variar mucho. Repetir la permutación y promediar las medidas de importancia sobre las repeticiones estabiliza la medida, pero aumenta el tiempo de cálculo.

Si las características están correlacionadas, la importancia de la característica de permutación puede estar sesgada por instancias de datos poco realistas. El problema es el mismo que con gráficos de dependencia parcial: La permutación de características produce instancias de datos poco probables cuando dos o más características están correlacionadas. Cuando se correlacionan positivamente (como la altura y el peso de una persona) y barajo una de las características, creo nuevas instancias que son poco probables o incluso físicamente imposibles (por ejemplo, una persona de 2 metros con un peso de 30 kg), pero uso estas nuevas instancias para medir la importancia. En otras palabras, por la importancia de la característica de permutación de una característica correlacionada, consideramos cuánto disminuye el rendimiento del modelo cuando intercambiamos la característica con valores que nunca observaríamos en la realidad. Comprueba si las características están fuertemente correlacionadas y ten cuidado con la interpretación de la importancia de la característica si lo están.

Otra dificultad: Agregar una función correlacionada puede disminuir la importancia de la función asociada al dividir la importancia entre ambas características. Permíteme darte un ejemplo de lo que quiero decir con “dividir” la importancia de la característica: Queremos predecir la probabilidad de lluvia y usar la temperatura a las 8:00 a.m. del día anterior como una característica junto con otras características no correlacionadas. Entreno un random forest y resulta que la temperatura es la característica más importante y todo está bien y duermo bien la noche siguiente. Ahora imagina otro escenario en el que también incluyo la temperatura a las 9:00 a.m. como una característica que está fuertemente correlacionada con la temperatura a las 8:00 a.m. La temperatura a las 9:00 a.m. no me da mucha información adicional si ya conozco la temperatura a las 8:00 a.m. Pero tener más características siempre es bueno, ¿verdad? Entreno un random forest con las dos características de temperatura y las características no correlacionadas. Algunos de los árboles en el random forest recogen la temperatura de las 8:00 a.m., otros la temperatura de las 9:00 a.m., otra vez ambos y otra vez ninguno. Las dos características de temperatura juntas tienen un poco más importancia que la característica de temperatura única anterior, pero en lugar de estar en la parte superior de la lista de características importantes, cada temperatura ahora está en algún lugar en el medio. Al introducir una característica correlacionada, pateé la característica más importante desde la parte superior de la escala de importancia hasta la mediocridad. Por un lado, esto está bien, porque simplemente refleja el comportamiento del modelo de aprendizaje automático subyacente, aquí el random forest. La temperatura de las 8:00 a.m. simplemente se ha vuelto menos importante porque el modelo ahora puede confiar también en la medición a las 9:00 a.m. Por otro lado, hace que la interpretación de la importancia de la característica sea considerablemente más difícil. Imagina que deseas verificar las características de los errores de medición. La verificación es costosa, por lo que decides verificar solo las 3 características principales más importantes. En el primer caso verificarías la temperatura, en el segundo caso no incluirías ninguna característica de temperatura solo porque ahora comparten la importancia. Aunque los valores de importancia pueden tener sentido en el nivel de comportamiento del modelo, es confuso si hay características correlacionadas.

5.5.6 Software y alternativas

El paquete iml R se utilizó para los ejemplos. Los paquetes R DALEX yvip, así como la biblioteca Python alibi, también implementan la importancia de la característica de permutación independiente del modelo.

Un algoritmo llamado PIMP adapta el algoritmo de importancia de la característica para proporcionar valores p para las importancias.

---

34. Breiman, Leo. “Random Forests.” Machine Learning 45 (1). Springer: 5-32 (2001).↩

35. Fisher, Aaron, Cynthia Rudin, and Francesca Dominici. “Model Class Reliance: Variable importance measures for any machine learning model class, from the ‘Rashomon’ perspective.” http://arxiv.org/abs/1801.01489 (2018).↩