5.1 Diagrama de dependencia parcial (PDP)
El gráfico de dependencia parcial (PDP o gráfico de PD) muestra el efecto marginal que una o dos características tienen sobre el resultado previsto de un modelo de aprendizaje automático (J. H. Friedman 200126). Un gráfico de dependencia parcial puede mostrar si la relación entre el objetivo y una característica es lineal, monótona o más compleja. Por ejemplo, cuando se aplica a un modelo de regresión lineal, los gráficos de dependencia parcial siempre muestran una relación lineal.
La función de dependencia parcial para la regresión se define como:
\[\hat{f}_{x_S}(x_S)=E_{x_C}\left[\hat{f}(x_S,x_C)\right]=\int\hat{f}(x_S,x_C)d\mathbb{P}(x_C)\]
\(X_S\) son las características para las cuales se debe trazar la función de dependencia parcial y \(x_C\) son las otras características utilizadas en el modelo de aprendizaje automático \(\hat{f}\). Por lo general, solo hay una o dos características en el conjunto S. Las características en S son aquellas para las que queremos saber el efecto en la predicción. Los vectores de características \(x_S\) y \(x_C\) combinados forman el espacio total de características x. La dependencia parcial funciona al marginar la salida del modelo de aprendizaje automático sobre la distribución de las características en el conjunto C, de modo que la función muestra la relación entre las características en el conjunto S que nos interesan y el resultado previsto. Al marginar sobre las otras características, obtenemos una función que depende solo de las características en S, incluidas las interacciones con otras características.
La función parcial \(\hat{f}_{x_S}\) se calcula calculando promedios en los datos de entrenamiento, también conocido como método Monte Carlo:
\[\hat{f}_{x_S}(x_S)=\frac{1}{n}\sum_{i=1}^n\hat{f}(x_S,x^{(i)}_{C})\] La función parcial nos dice para los valores dados de las características S cuál es el efecto marginal promedio en la predicción. En esta fórmula, \(x^{(i)}_{C}\) son valores de características reales del conjunto de datos para las características en las que no estamos interesados, y n es el número de instancias en el conjunto de datos. Una suposición del PDP es que las características en C no están correlacionadas con las características en S. Si se viola este supuesto, los promedios calculados para el gráfico de dependencia parcial incluirán puntos de datos que son muy improbables o incluso imposibles (ver desventajas).
Para la clasificación en la que el modelo de aprendizaje automático genera probabilidades, el gráfico de dependencia parcial muestra la probabilidad de una determinada clase dados diferentes valores para las características en S. Una manera fácil de lidiar con múltiples clases es dibujar una línea o diagrama por clase.
El diagrama de dependencia parcial es un método global: El método considera todas las instancias y ofrece una declaración sobre la relación global de una característica con el resultado previsto.
Características categóricas
Hasta ahora, solo hemos considerado las características numéricas. Para características categóricas, la dependencia parcial es muy fácil de calcular. Para cada una de las categorías, obtenemos una estimación de PDP al obligar a todas las instancias de datos a tener la misma categoría. Por ejemplo, si observamos el conjunto de datos de alquiler de bicicletas y estamos interesados en el gráfico de dependencia parcial para la temporada, obtenemos 4 números, uno para cada temporada. Para calcular el valor de “verano”, reemplazamos la temporada de todas las instancias de datos con “verano” y promediamos las predicciones.
5.1.1 Ejemplos
En la práctica, el conjunto de características S generalmente solo contiene una característica o un máximo de dos, porque una característica produce gráficos 2D y dos características producen gráficos 3D. Todo lo que está más allá de eso es bastante complicado. Incluso 3D en un papel o monitor 2D ya es un desafío.
Volvamos al ejemplo de regresión, en el que predecimos el número de bicicletas que se alquilarán en un día determinado. Primero ajustamos un modelo de aprendizaje automático, luego analizamos las dependencias parciales. En este caso, hemos ajustado un random forest para predecir el número de bicicletas y utilizar el diagrama de dependencia parcial para visualizar las relaciones que el modelo ha aprendido. La influencia de las características climáticas en el conteo previsto de bicicletas se visualiza en la siguiente figura.
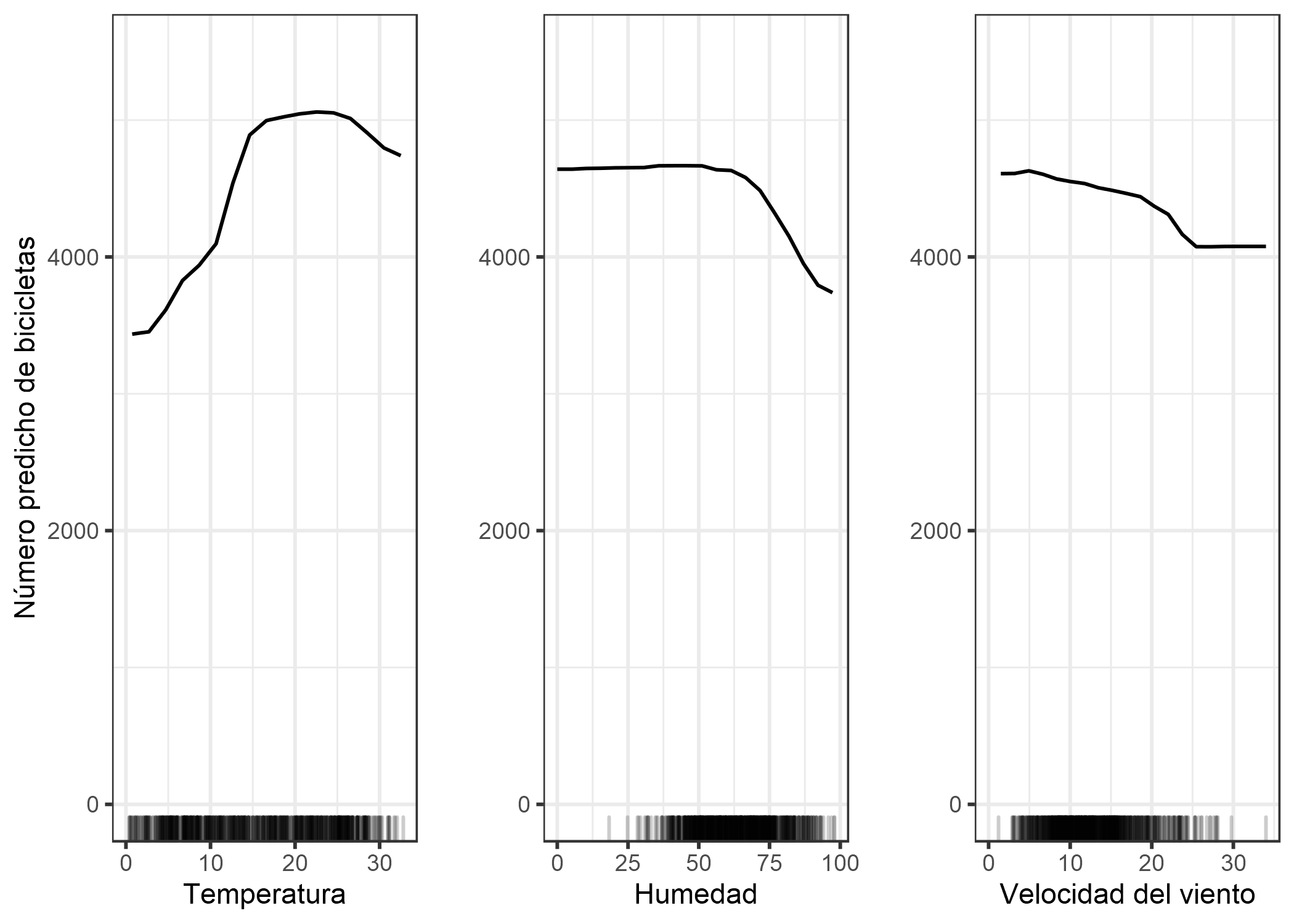
FIGURA 5.2: PDP para el modelo de predicción de conteo de bicicletas y temperatura, humedad y velocidad del viento. Las mayores diferencias se pueden ver en la temperatura. Cuanto más caliente, más bicicletas se alquilan. Esta tendencia sube a 20 grados centígrados, luego se aplana y cae ligeramente a 30. Las marcas en el eje x indican la distribución de datos.
Para clima cálido pero no demasiado caluroso, el modelo predice en promedio un gran número de bicicletas alquiladas. Los ciclistas potenciales se inhiben cada vez más en el alquiler de una bicicleta cuando la humedad supera el 60%. Además, cuanto más viento, a menos personas les gusta andar en bicicleta, lo que tiene sentido. Curiosamente, el número previsto de alquileres de bicicletas no disminuye cuando la velocidad del viento aumenta de 25 a 35 km/h, pero no hay muchos datos de entrenamiento, por lo que el modelo de aprendizaje automático probablemente no pueda obtener una predicción significativa para este rango. Al menos intuitivamente, esperaría que la cantidad de bicicletas disminuya al aumentar la velocidad del viento, especialmente cuando la velocidad del viento es muy alta.
Para ilustrar un diagrama de dependencia parcial con una característica categórica, examinamos el efecto de la característica de temporada en el alquiler de bicicletas previsto.
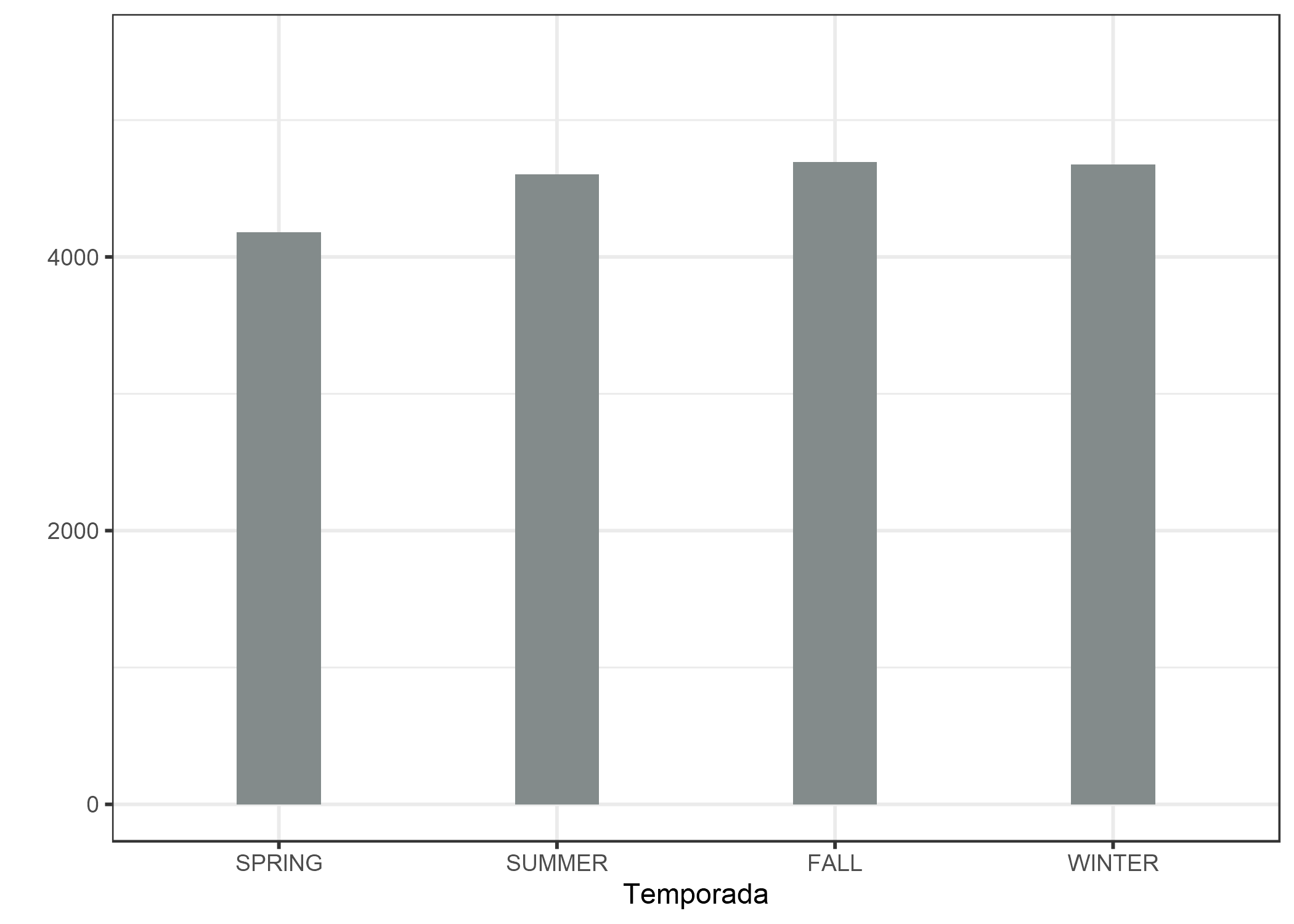
FIGURA 5.3: PDP para el modelo de predicción de conteo de bicicletas y la temporada. Inesperadamente, todas las estaciones muestran un efecto similar en las predicciones del modelo, solo para la primavera, el modelo predice menos alquileres de bicicletas.
También calculamos la dependencia parcial para clasificación de cáncer cervical. Esta vez, ajustamos un random forest para predecir si una mujer podría contraer cáncer cervical en función de los factores de riesgo. Calculamos y visualizamos la dependencia parcial de la probabilidad de cáncer de diferentes características para el random forest:
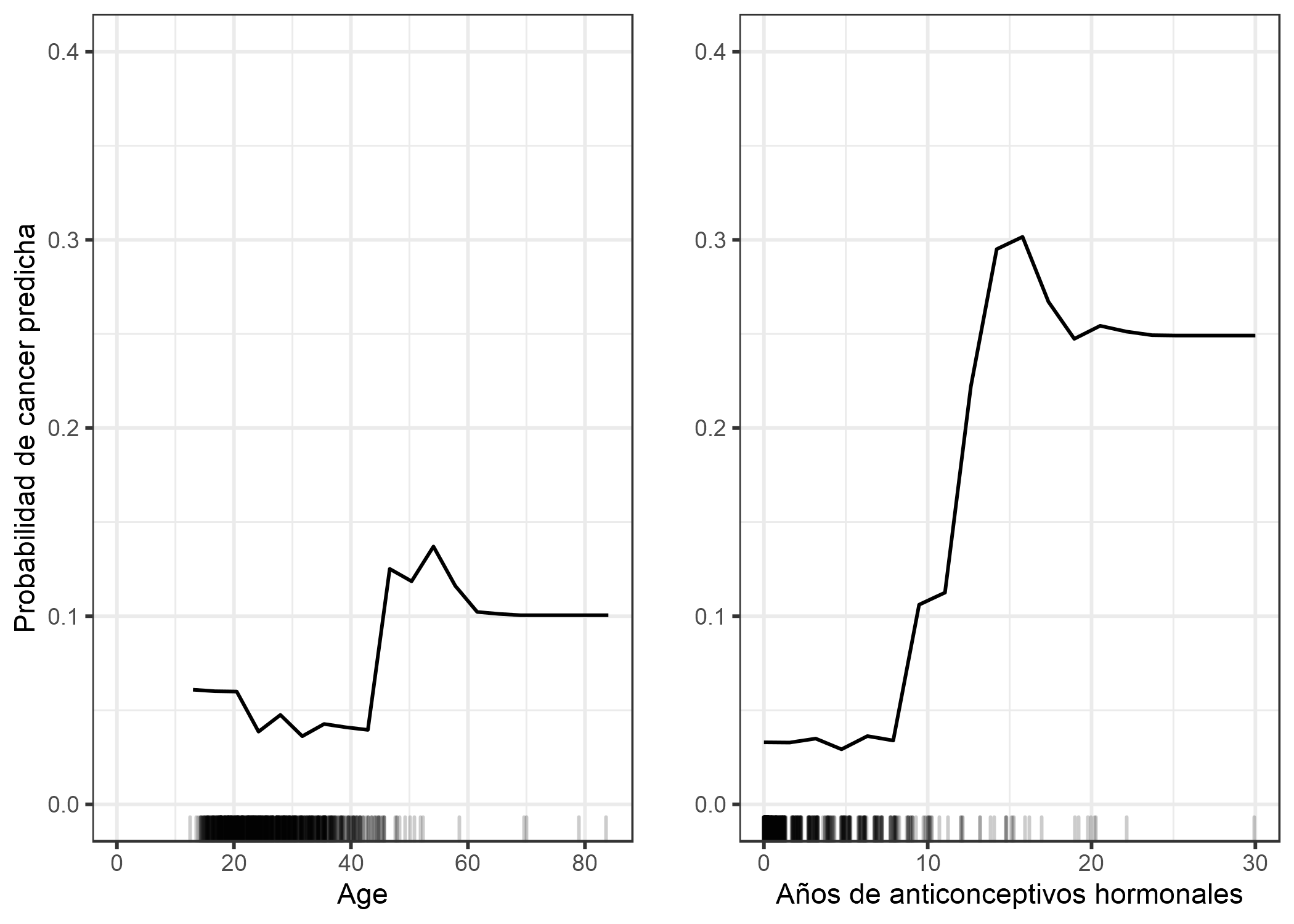
FIGURA 5.4: PDP de probabilidad de cáncer según la edad y años con anticonceptivos hormonales. Para la edad, el PDP muestra que la probabilidad es baja hasta los 40 y aumenta después. Cuantos más años con anticonceptivos hormonales, mayor será el riesgo de cáncer previsto, especialmente después de 10 años. Para ambas características, no había muchos puntos de datos con valores grandes disponibles, por lo que las estimaciones de PD son menos confiables en esas regiones.
También podemos visualizar la dependencia parcial de dos características a la vez:
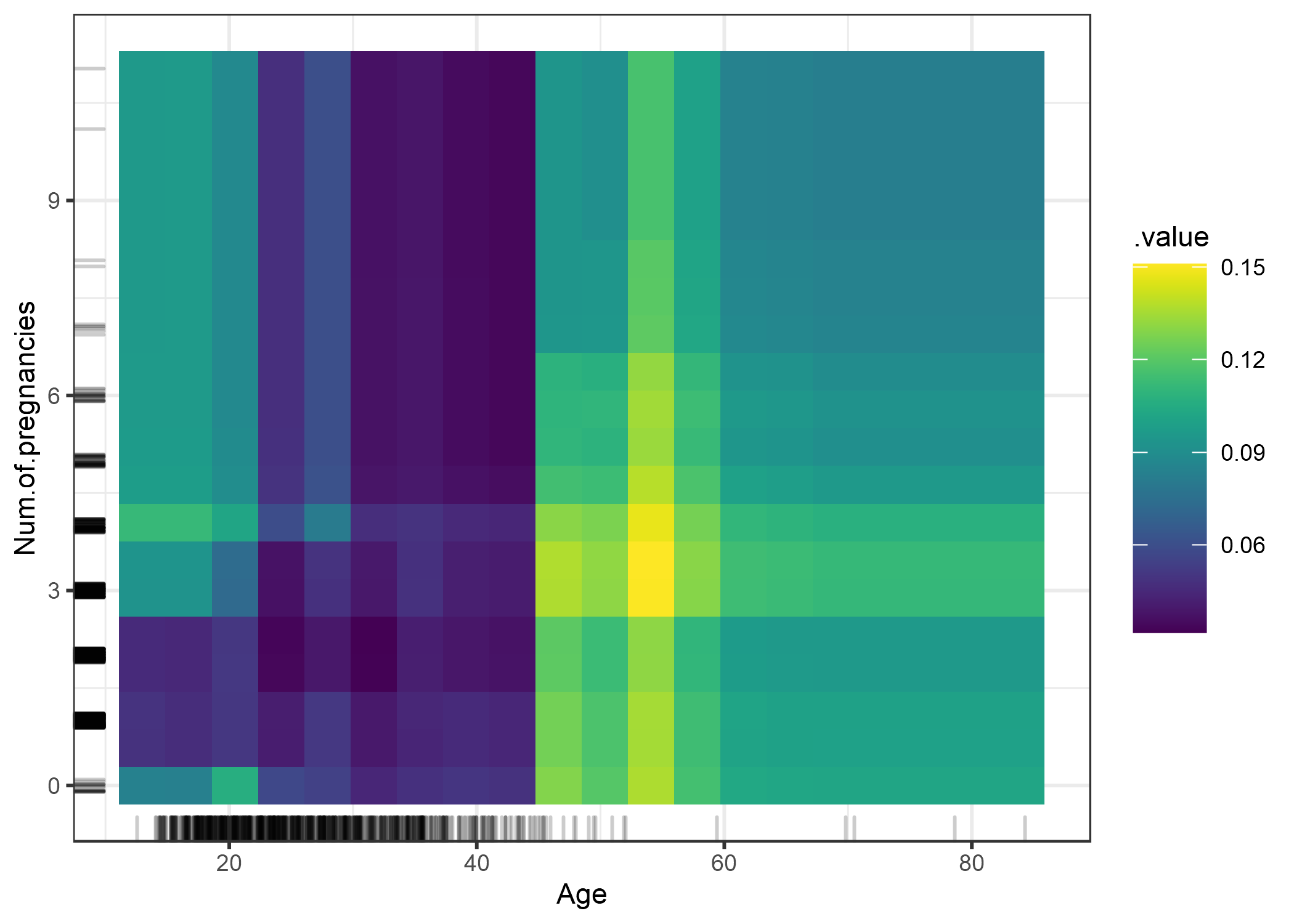
FIGURA 5.5: PDP de probabilidad de cáncer y la interacción de la edad y el número de embarazos. El gráfico muestra el aumento en la probabilidad de cáncer a los 45 años. Para las edades menores de 25 años, las mujeres que tuvieron 1 o 2 embarazos tienen un riesgo de cáncer más bajo previsto, en comparación con las mujeres que tuvieron 0 o más de 2 embarazos. Pero ten cuidado al sacar conclusiones: ¡Esto podría ser una correlación no causal!
5.1.2 Ventajas
El cálculo de los gráficos de dependencia parcial es intuitivo: La función de dependencia parcial en un valor de característica particular representa la predicción promedio si forzamos a todos los puntos de datos a asumir ese valor de característica. En mi experiencia, los laicos generalmente entienden la idea de PDP rápidamente.
Si la característica para la que calculó el PDP no está correlacionada con las otras características, entonces los PDP representan perfectamente cómo la característica influye en la predicción en promedio. En el caso no correlacionado, la interpretación es clara: El gráfico de dependencia parcial muestra cómo cambia la predicción promedio en su conjunto de datos cuando se cambia la característica j-ésima. Es más complicado cuando las características están correlacionadas, ver también desventajas.
Las gráficas de dependencia parcial son fáciles de implementar.
El cálculo para los gráficos de dependencia parcial tiene una interpretación causal. Intervenimos en una característica y medimos los cambios en las predicciones. Al hacerlo, analizamos la relación causal entre la característica y la predicción. 27 La relación es causal para el modelo, porque modelamos explícitamente el resultado en función de las características, ¡pero no necesariamente para el mundo real!
5.1.3 Desventajas
El número máximo realista de características en una función de dependencia parcial es dos. Esto no es culpa de los PDP, sino de la representación bidimensional (papel o pantalla) y también de nuestra incapacidad para imaginar más de 3 dimensiones.
Algunos gráficos de PD no muestran la distribución de características. Omitir la distribución puede ser engañoso, porque podría sobreinterpretar regiones sin casi datos. Este problema se resuelve fácilmente mostrando una alfombra (indicadores para puntos de datos en el eje x) o un histograma.
La suposición de independencia es el mayor problema con los PDP. Se supone que las características para las que se calcula la dependencia parcial no están correlacionadas con otras características. Por ejemplo, supón que deseas predecir qué tan rápido camina una persona, dado el peso y la altura. Para la dependencia parcial de una de las características, por ejemplo altura, suponemos que las otras características (peso) no están correlacionadas con la altura, lo que obviamente es una suposición falsa. Para el cálculo del PDP a cierta altura (por ejemplo, 200 cm), promediamos la distribución marginal de peso, que podría incluir un peso por debajo de 50 kg, lo que no es realista para una persona de 2 metros. En otras palabras: Cuando las características están correlacionadas, creamos nuevos puntos de datos en áreas de la distribución de características donde la probabilidad real es muy baja (por ejemplo, es poco probable que alguien mida 2 metros de altura pero pese menos de 50 kg). Una solución a este problema es Gráficos de efectos locales acumulados o gráficos ALE cortos que funcionan con la distribución condicional en lugar de la marginal.
Los efectos heterogéneos pueden estar ocultos porque las gráficas PD solo muestran los efectos marginales promedio. Supón que para una característica, la mitad de sus puntos de datos tienen una asociación positiva con la predicción (cuanto mayor es el valor de la característica, mayor es la predicción) y la otra mitad tiene una asociación negativa: cuanto menor es el valor de la característica, mayor es la predicción. La curva PD podría ser una línea horizontal, ya que los efectos de ambas mitades del conjunto de datos podrían cancelarse entre sí. Luego concluye que la función no tiene efecto en la predicción. Al trazar las curvas de expectativas condicionales individuales en lugar de la línea agregada, podemos descubrir efectos heterogéneos.
5.1.4 Software y alternativas
Hay varios paquetes R que implementan PDP.
Usé el paquete iml para los ejemplos, pero también haypdp o DALEX.
En Python, las gráficas de dependencia parcial están integradas en scikit-learn y puede usarPDPBox.
Las alternativas a los PDP presentados en este libro son gráficos ALE y curvas ICE.