4.1 Regresión lineal

Un modelo de regresión lineal predice el objetivo como una suma ponderada de las entradas de características. La linealidad de la relación facilita la interpretación. Los modelos de regresión lineal son utilizados por estadísticos, informáticos y otras personas que abordan problemas cuantitativos.

Los modelos lineales se pueden usar para modelar la dependencia de un objetivo de regresión y de algunas características x. Las relaciones aprendidas son lineales y se pueden escribir para una sola instancia i de la siguiente manera:

\[y=\beta_{0}+\beta_{1}x_{1}+\ldots+\beta_{p}x_{p}+\epsilon\]

El resultado previsto de una instancia es una suma ponderada de sus características p. Los betas (\(\beta_{j}\)) representan los pesos o coeficientes de las características aprendidas. El primer peso en la suma (\(\beta_0\)) se denomina intercepto y no se multiplica con un valor de característica. El épsilon (\(\epsilon\)) es el error que cometemos, es decir, la diferencia entre la predicción y el resultado real. Se supone que estos errores siguen una distribución gaussiana, lo que significa que cometemos errores en direcciones negativas y positivas y cometemos muchos errores pequeños y pocos errores grandes.

Se pueden usar varios métodos para estimar el peso óptimo. El método de mínimos cuadrados ordinarios generalmente se usa para encontrar los pesos que minimizan las diferencias al cuadrado entre los resultados reales y los estimados:

\[\hat{\boldsymbol{\beta}}=\arg\!\min_{\beta_0,\ldots,\beta_p}\sum_{i=1}^n\left(y^{(i)}-\left(\beta_0+\sum_{j=1}^p\beta_jx^{(i)}_{j}\right)\right)^{2}\]

No discutiremos en detalle cómo se pueden encontrar los pesos óptimos, pero si estás interesado, puedes leer el capítulo 3.2 del libro “Los elementos del aprendizaje estadístico” (Friedman, Hastie y Tibshirani 2009)¹⁶ o uno de los otros recursos en línea sobre modelos de regresión lineal.

La mayor ventaja de los modelos de regresión lineal es la linealidad: Simplifica el procedimiento de estimación y, lo que es más importante, estas ecuaciones lineales tienen una interpretación fácil de entender a nivel modular (es decir, los pesos). Esta es una de las principales razones por las que el modelo lineal y todos los modelos similares están tan extendidos en campos académicos como la medicina, la sociología, la psicología y muchos otros campos de investigación cuantitativa. Por ejemplo, en el campo de la medicina, no solo es importante predecir el resultado clínico de un paciente, sino también cuantificar la influencia del fármaco y al mismo tiempo tener en cuenta el sexo, la edad y otras características de manera interpretable.

Los pesos estimados vienen con intervalos de confianza. Un intervalo de confianza es un rango para la estimación de peso que cubre el peso “verdadero” con una cierta confianza. Por ejemplo, un intervalo de confianza del 95% para un peso de 2 podría variar de 1 a 3. La interpretación de este intervalo sería: Si repetimos la estimación 100 veces con datos recién muestreados, el intervalo de confianza incluiría el peso verdadero en 95 de los 100 casos, dado que el modelo de regresión lineal es el modelo correcto para los datos.

Si el modelo es el modelo “correcto” depende de si las relaciones en los datos cumplen ciertos supuestos, que son linealidad, normalidad, homocedasticidad, independencia, características fijas y ausencia de multicolinealidad.

Linealidad

El modelo de regresión lineal obliga a la predicción a ser una combinación lineal de características, que es tanto su mayor fortaleza como su mayor limitación. La linealidad conduce a modelos interpretables. Los efectos lineales son fáciles de cuantificar y describir. Son aditivos, por lo que es fácil separar los efectos. Si sospechas interacciones de entidades o una asociación no lineal de una entidad con el valor objetivo, puedes agregar términos de interacción o utilizar splines de regresión.

Normalidad

Se supone que el resultado objetivo dadas las características sigue una distribución normal. Si se viola esta suposición, los intervalos de confianza estimados de los pesos de las características no son válidos.

Homocedasticidad (varianza constante)

Se supone que la varianza de los términos de error es constante en todo el espacio de características. Supón que deseas predecir el valor de una casa dada la superficie habitable en metros cuadrados. Estimas un modelo lineal que asume que, independientemente del tamaño de la casa, el error en torno a la respuesta pronosticada tiene la misma variación. Esta suposición a menudo se viola en la realidad. En el ejemplo de la casa, es plausible que la variación de los términos de error alrededor del precio predicho sea mayor para las casas más grandes, ya que los precios son más altos y hay más margen para las fluctuaciones de precios. Supón que el error promedio (diferencia entre el precio predicho y el real) en su modelo de regresión lineal es de 50,000 euros. Si asumes la homocedasticidad, asumes que el error promedio de 50,000 es el mismo para casas que cuestan 1 millón y para casas que cuestan solo 40,000. Esto no es razonable, porque significaría que podemos esperar precios de vivienda negativos.

Independencia

Se supone que cada observación es independiente de cualquier otra observación. Si realizas mediciones repetidas, como múltiples análisis de sangre por paciente, las observaciones no son independientes. Para datos dependientes necesitas modelos especiales de regresión lineal, como modelos de efectos mixtos, GLMM o GEE. Si usas el modelo de regresión lineal “normal”, puedes sacar conclusiones incorrectas del modelo.

Características fijas

Las características de entrada se consideran “fijas”. Fijo significa que se tratan como “constantes dadas” y no como variables estadísticas. Esto implica que están libres de errores de medición. Esta es una suposición poco realista. Sin ese supuesto, sin embargo, tendrías que adaptarte a modelos de error de medición muy complejos que tengan en cuenta los errores de medición de sus características de entrada. Y generalmente no quieres hacer eso.

Ausencia de multicolinealidad

No deseas características fuertemente correlacionadas, porque esto arruina la estimación de los pesos. En una situación en la que dos características están fuertemente correlacionadas, se vuelve problemático estimar los pesos porque los efectos de la característica son aditivos y se vuelve indeterminable a cuál de las características correlacionadas atribuir los efectos.

4.1.1 Interpretación

La interpretación de una ponderación en el modelo de regresión lineal depende del tipo de la característica correspondiente.

• Característica numérica: aumentar la característica numérica en una unidad cambia el resultado estimado por su peso. Un ejemplo de una característica numérica es el tamaño de una casa.
• Característica binaria: una característica que toma uno de los dos valores posibles para cada instancia. Un ejemplo es la característica “La casa viene con un jardín”. Uno de los valores cuenta como la categoría basal (en algunos lenguajes de programación codificados con 0), como “Sin jardín”. Cambiar la característica de la categoría basal a la otra categoría cambia el resultado estimado por el peso de la característica.
• Característica categórica con múltiples categorías: Una característica con un número fijo de valores posibles. Un ejemplo es la característica “tipo de piso”, con posibles categorías “alfombra”, “laminado” y “parquet”. Una solución para tratar con muchas categorías es la codificación en caliente -hot encoding-, lo que significa que cada categoría tiene su propia columna binaria. Para una característica categórica con categorías L, solo necesitas L-1 columnas, porque la columna restante tendría información redundante (por ejemplo, cuando las columnas 1 a L-1 tienen valor 0 para una instancia, sabemos que el valor de esa variable es el de la categoría restante). La interpretación para cada categoría es entonces la misma que la interpretación para las características binarias. Algunos lenguajes, como R, permiten codificar características categóricas de varias maneras, como se describe más adelante en este capítulo.
• Intercepto \(\beta_0\): El intercepto es el peso de la característica para la “característica constante”, que siempre es 1 para todas las instancias. La mayoría de los paquetes de software agregan automáticamente esta característica “1” para estimar la intercepción. La interpretación es: Para una instancia con todos los valores de características numéricas en cero y los valores de características categóricas en las categorías de referencia, la predicción del modelo es el peso del intercepto. La interpretación del intercepto generalmente no es relevante porque las instancias con todos los valores de características en cero a menudo no tienen sentido. La interpretación solo es significativa cuando las características se han estandarizado (media de cero, desviación estándar de uno). En estos casos, el intercepto refleja el resultado previsto de una instancia en la que todas las características tienen su valor medio.

La interpretación de las características en el modelo de regresión lineal se puede automatizar mediante el uso de las siguientes plantillas de texto.

Interpretación de una característica numérica

Un aumento de la característica \(x_ {k}\) en una unidad aumenta la predicción para y en \(\beta_k\) unidades cuando todos los demás valores de la característica permanecen fijos.

Interpretación de una característica categórica

Cambiar la característica \(x_{k}\) de la categoría de referencia a la otra categoría aumenta la predicción para y en \(\beta_{k}\) cuando todas las demás funciones permanecen fijas.

Otra medida importante para interpretar modelos lineales es la medición de R cuadrado. Esta medida te indica qué cantidad de la varianza total de tu resultado objetivo es explicada por el modelo. Cuanto mayor sea el R cuadrado, mejor explicará tu modelo los datos. La fórmula para calcular el R-cuadrado es:

\[R^2=1-SSE/SST\]

SSE es la suma al cuadrado de los términos de error:

\[SSE=\sum_{i=1}^n(y^{(i)}-\hat{y}^{(i)})^2\]

SST es la suma al cuadrado de la varianza de datos:

\[SST=\sum_{i=1}^n(y^{(i)}-\bar{y})^2\]

El SSE te indica cuánta varianza queda después de ajustar el modelo lineal, que se mide por las diferencias al cuadrado entre los valores objetivo predichos y reales. SST es la varianza total del resultado objetivo. El R-cuadrado te indica cuánta de tu varianza puede explicarse por el modelo lineal. El R-cuadrado varía entre 0 para modelos donde el modelo no explica los datos en absoluto y 1 para los modelos que explican toda la varianza en sus datos.

Hay un problema, porque el R-cuadrado aumenta con el número de características en el modelo, incluso si no contienen ninguna información sobre el valor objetivo en absoluto. Por lo tanto, es mejor usar el R cuadrado ajustado, que representa la cantidad de características utilizadas en el modelo. Su cálculo es:

\[\bar{R}^2=R^2-(1-R^2)\frac{n-1}{n-p-1}\]

donde p es el número de características y n el número de instancias.

No tiene sentido interpretar un modelo con un R cuadrado muy bajo (ajustado), porque dicho modelo básicamente no explica gran parte de la varianza. Cualquier interpretación de los pesos no sería significativa.

Importancia de la característica

La importancia de una característica en un modelo de regresión lineal se puede medir por el valor absoluto de su estadístico t. El estadístico t es el peso estimado escalado con su error estándar.

\[t_{\hat{\beta}_j}=\frac{\hat{\beta}_j}{SE(\hat{\beta}_j)}\]

Examinemos lo que esta fórmula nos dice: La importancia de una característica aumenta con el aumento de peso. Esto tiene sentido. Mientras más varianza tenga el peso estimado (= menos seguro estamos del valor correcto), menos importante es la característica. Esto también tiene sentido.

4.1.2 Ejemplo

En este ejemplo, utilizamos el modelo de regresión lineal para predecir el número de bicicletas alquiladas en un día en particular, dada la información del clima y el calendario. Para la interpretación, examinamos los pesos de regresión estimados. Las características se reparten entre numéricas y categóricas. Para cada característica, la tabla muestra el peso estimado, el error estándar de la estimación (SE) y el valor absoluto del estadístico t (|t|).

	Weight	SE	|t|
(Intercept)	2399.4	238.3	10.1
seasonSUMMER	899.3	122.3	7.4
seasonFALL	138.2	161.7	0.9
seasonWINTER	425.6	110.8	3.8
holidayHOLIDAY	-686.1	203.3	3.4
workingdayWORKING DAY	124.9	73.3	1.7
weathersitMISTY	-379.4	87.6	4.3
weathersitRAIN/SNOW/STORM	-1901.5	223.6	8.5
temp	110.7	7.0	15.7
hum	-17.4	3.2	5.5
windspeed	-42.5	6.9	6.2
days_since_2011	4.9	0.2	28.5

Interpretación de una característica numérica (temperatura): Un aumento de la temperatura en 1 grado Celsius aumenta el número previsto de bicicletas en 110.7, cuando todas las demás características permanecen fijas.

Interpretación de una característica categórica (“weathersit”): El número estimado de bicicletas es -1901.5 más bajo cuando está lloviendo, nevando o tormentoso, en comparación con el buen tiempo - suponiendo nuevamente que todas las demás características no cambian. Cuando el clima es brumoso, el número previsto de bicicletas es -379.4 menor en comparación con el buen clima, dado que todas las demás características siguen siendo las mismas.

Todas las interpretaciones siempre vienen con la nota al pie de página de que “todas las demás características siguen siendo las mismas”. Esto se debe a la naturaleza de los modelos de regresión lineal. El objetivo previsto es una combinación lineal de las características ponderadas. La ecuación lineal estimada es un hiperplano en el espacio característica / objetivo (una línea simple en el caso de una característica única). Los pesos especifican la pendiente (gradiente) del hiperplano en cada dirección. El lado bueno es que la aditividad aísla la interpretación de un efecto de característica individual de todas las demás características. Eso es posible porque todos los efectos de la característica (= peso por valor de la característica) en la ecuación se combinan con un signo más. En el lado negativo de las cosas, la interpretación ignora la distribución conjunta de las características. Aumentar una característica, pero no cambiar otra, puede conducir a puntos de datos poco realistas o al menos improbables. Por ejemplo, aumentar el número de habitaciones puede ser poco realista sin aumentar también el tamaño de una casa.

4.1.3 Interpretación visual

Varias visualizaciones hacen que el modelo de regresión lineal sea fácil y rápido de comprender para los humanos.

4.1.3.1 Gráfica de peso

La información de la tabla de peso (estimaciones de peso y varianza) se puede visualizar en un gráfico de peso. La siguiente gráfica muestra los resultados del modelo de regresión lineal anterior.

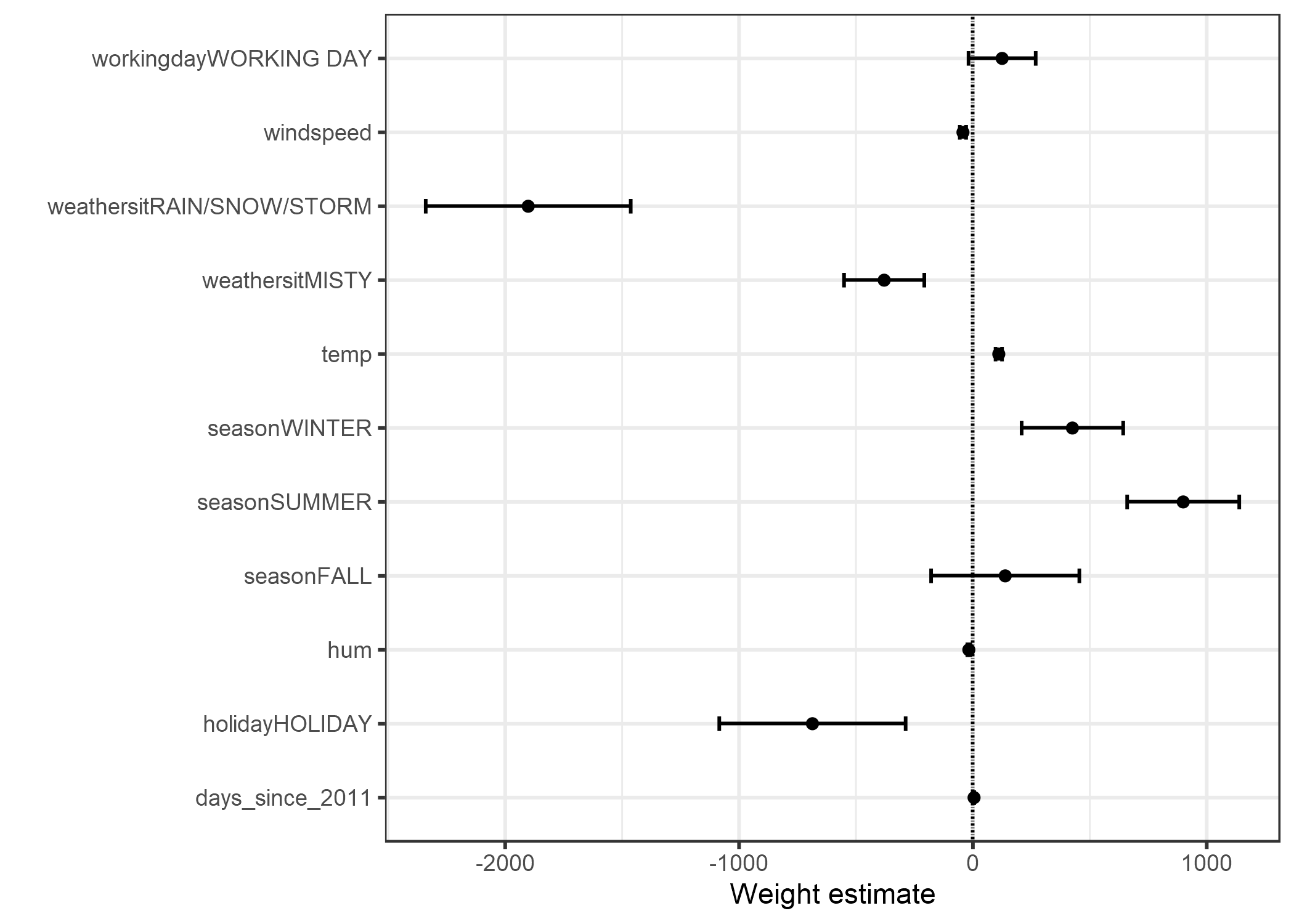
FIGURA 4.1: Los pesos estimados se muestran en los puntos, y los intervalos del 95% de confianza se muestran en las líneas.

La gráfica de peso muestra que el clima lluvioso / nevoso / tormentoso tiene un fuerte efecto negativo en el número previsto de bicicletas. El peso de la característica de día laborable es cercano a cero y se incluye cero en el intervalo del 95%, lo que significa que el efecto no es estadísticamente significativo. Algunos intervalos de confianza son muy cortos y las estimaciones son cercanas a cero, aunque los efectos característicos fueron estadísticamente significativos. La temperatura es uno de esos candidatos. El problema con la gráfica de peso es que las características se miden en diferentes escalas. Mientras que para el clima el peso estimado refleja la diferencia entre el clima bueno y lluvioso / tormentoso / nevado, para la temperatura solo refleja un aumento de 1 grado Celsius. Puedes hacer los pesos más comparables al escalar las características (media cero y desviación estándar de uno) antes de ajustar el modelo lineal.

4.1.3.2 Gráfico de efectos

Los pesos del modelo de regresión lineal pueden analizarse de manera más significativa cuando se multiplican por los valores reales de la característica. Los pesos dependen de la escala de las funciones y serán distintos, si tienes una variable que mida la altura de una persona y cambias de metro a centímetro. El peso cambiará, pero los efectos reales en sus datos no lo harán. También es importante conocer la distribución de su característica en los datos, porque si tiene una variación muy baja, significa que casi todas las instancias tienen una contribución similar de esta característica. La gráfica de efectos puede ayudarte a comprender cuánto contribuye la combinación de peso y función a las predicciones en sus datos. Comienza calculando los efectos, que es el peso por característica multiplicado por el valor de característica de una instancia:

\[\text{effect}_{j}^{(i)}=w_{j}x_{j}^{(i)}\]

Los efectos se pueden visualizar con diagramas de caja. Una caja contiene el rango de efectos para la mitad de sus datos (cuantiles de efectos del 25% al 75%). La línea vertical en el cuadro es el efecto medio, es decir, el 50% de las instancias tienen un efecto más bajo y la otra mitad más alto en la predicción. Las líneas horizontales se extienden a \(\pm1.5\text{IQR}/\sqrt{n}\), siendo IQR el rango intercuartil (Q3 menos Q1). Los puntos son valores atípicos. Los efectos de características categóricas se pueden resumir en una sola gráfica de caja, en comparación con la gráfica de peso, donde cada categoría tiene su propia fila.

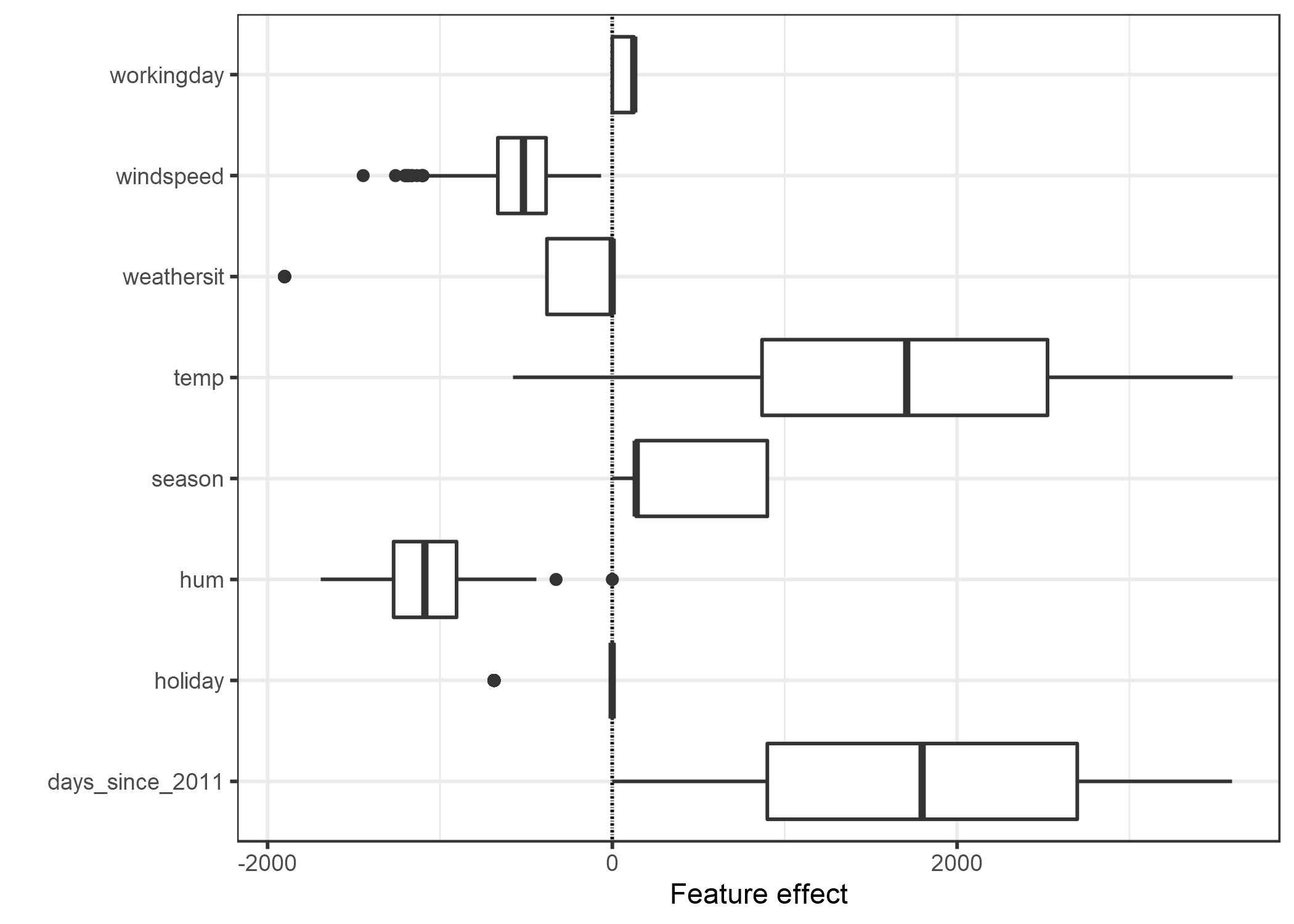
FIGURA 4.2: El gráfico de efectos de características muestra la distribución de los efectos (=valor de característica veces peso de característica) en los datos, por característica.

Las mayores contribuciones al número esperado de bicicletas alquiladas provienen de la variable de temperatura y la variable de días, que captura la tendencia del alquiler de bicicletas con el tiempo. La temperatura tiene un amplio rango de cuánto contribuye a la predicción. La característica de tendencia del día va de cero a grandes contribuciones positivas, porque el primer día en el conjunto de datos (01.01.2011) tiene un efecto de tendencia muy pequeño y el peso estimado para esta característica es positivo (4.93). Esto significa que el efecto aumenta con cada día y es más alto para el último día en el conjunto de datos (31.12.2012). Ten en cuenta que para los efectos con un peso negativo, las observaciones con un efecto positivo son aquellas que tienen un valor de característica negativo. Por ejemplo, los días con un alto efecto negativo de la velocidad del viento son los que tienen altas velocidades del viento.

4.1.4 Explicación de predicciones individuales

¿Cuánto ha contribuido cada característica de una instancia a la predicción? Esto puede responderse calculando los efectos para esta instancia. Una interpretación de los efectos específicos de la observación solo tiene sentido en comparación con la distribución del efecto para cada característica. Queremos explicar la predicción del modelo lineal para la 6 observación del conjunto de datos de la bicicleta. La instancia tiene los siguientes valores de características.

Feature	Value
season	SPRING
yr	2011
mnth	JAN
holiday	NO HOLIDAY
weekday	THU
workingday	WORKING DAY
weathersit	GOOD
temp	1.604356
hum	51.8261
windspeed	6.000868
cnt	1606
days_since_2011	5

Para obtener los efectos de característica de esta instancia, tenemos que multiplicar sus valores de característica por los pesos correspondientes del modelo de regresión lineal. Para el valor “WORKING DAY” de la característica “workingday”, el efecto es, 124.9. Para una temperatura de 1.6 grados Celsius, el efecto es 177.6. Agregamos estos efectos individuales como cruces al gráfico de efectos, que nos muestra la distribución de los efectos en los datos. Esto nos permite comparar los efectos individuales con la distribución de efectos en los datos.

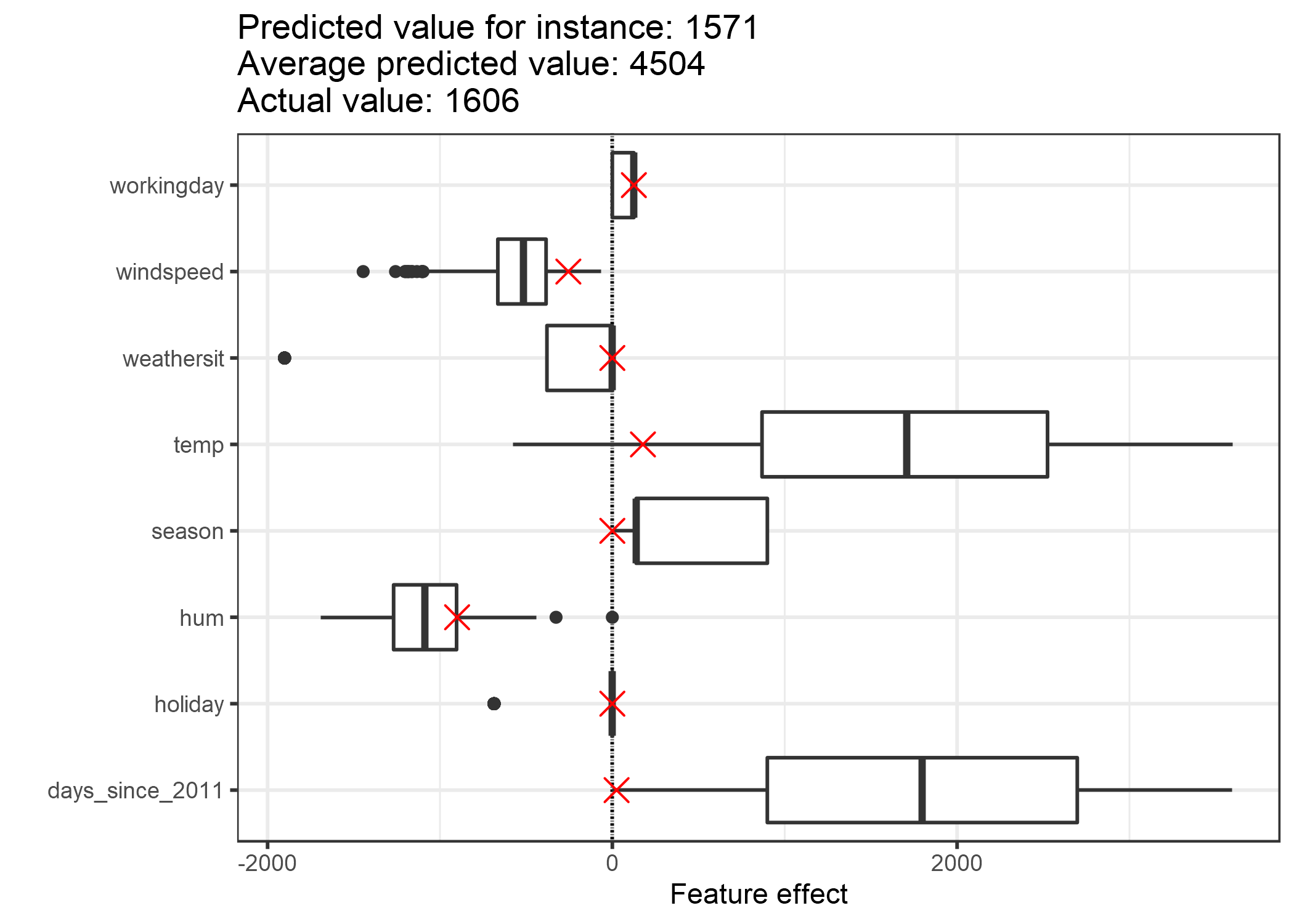
FIGURA 4.3: El gráfico de efectos para una observación muestra la distribución del efecto y marca con una cruz la instancia de interés.

Si promediamos las predicciones para las instancias de datos de entrenamiento, obtenemos un promedio de 4504. En comparación, la predicción de la instancia 6-ésima es pequeña, ya que solo se predicen 1571 alquileres de bicicletas. El gráfico de efectos revela la razón por la cual. Los diagramas de caja muestran las distribuciones de los efectos para todas las instancias del conjunto de datos, los cruces muestran los efectos para la instancia 6. La instancia 6 tiene un efecto de baja temperatura porque en este día la temperatura era de 2 grados, que es baja en comparación con la mayoría de los otros días (y recuerde que el peso de la característica de temperatura es positivo). Además, el efecto de la característica de tendencia “days_since_2011” es pequeño en comparación con otras instancias de datos porque esta instancia es de principios de 2011 (5 days) y la característica de tendencia también tiene un peso positivo.

4.1.5 Codificación de características categóricas

Hay varias formas de codificar una característica categórica, y la elección influye en la interpretación de los pesos.

El estándar en los modelos de regresión lineal es la codificación del tratamiento, que es suficiente en la mayoría de los casos. Usando diferentes codificaciones se reduce a crear diferentes matrices (de diseño) desde una sola columna con la variable categórica. Esta sección presenta tres codificaciones diferentes, pero hay muchas más. El ejemplo utilizado tiene seis instancias y una característica categórica con tres categorías. Para las dos primeras instancias, la característica toma la categoría A; para los casos tres y cuatro, categoría B; y para las dos últimas instancias, categoría C.

Codificación de tratamiento

En la codificación del tratamiento, el peso por categoría es la diferencia estimada en la predicción entre la categoría correspondiente y la categoría basal, o de referencia. El intercepto intersección del modelo lineal es la media de la categoría de referencia (cuando todas las demás características siguen siendo las mismas). La primera columna de la matriz de diseño es el intercepto, que siempre es 1. La columna dos indica si la instancia i está en la categoría B, la columna tres indica si está en la categoría C. No hay necesidad de una columna para la categoría A, porque entonces la ecuación lineal estaría sobreespecificada y no se puede encontrar una solución única para los pesos. Es suficiente saber que una instancia no está en la categoría B o C.

Matriz de características: \[\begin{pmatrix}1&0&0\\1&0&0\\1&1&0\\1&1&0\\1&0&1\\1&0&1\\\end{pmatrix}\]

Codificación de efecto

En la codificación de efecto, el peso por categoría es la diferencia en la y-estimada en la categoría correspondiente a la media general (dado que todas las demás características son cero o la categoría basal). La primera columna se usa para estimar la intersección. El peso \(\beta_{0}\) asociado con el intercepto representa la media general y \(\beta_{1}\), el peso de la columna dos, es la diferencia entre la media general y la categoría B. El efecto total de la categoría B es \(\beta_{0}+\beta_{1}\). La interpretación para la categoría C es equivalente. Para la categoría de referencia A, \(-(\beta_{1}+\beta_{2})\) es la diferencia con la media general y \(\beta_{0}-(\beta_{1}+\beta_{2})\) el efecto general.

Matriz de características: \[\begin{pmatrix}1&-1&-1\\1&-1&-1\\1&1&0\\1&1&0\\1&0&1\\1&0&1\\\end{pmatrix}\]

Codificación dummy

En la codificación dummy, el \(\beta\) por categoría es el valor medio estimado de y para cada categoría (dado que todos los demás valores de características son cero o la categoría basal). Ten en cuenta que la intersección se ha omitido aquí para que se pueda encontrar una solución única para los pesos del modelo lineal.

Matriz de características: \[\begin{pmatrix}1&0&0\\1&0&0\\0&1&0\\0&1&0\\0&0&1\\0&0&1\\\end{pmatrix}\]

Si deseas profundizar un poco más en las diferentes codificaciones de características categóricas, consulta esta página web de resumen y esta publicación de blog.

4.1.6 ¿Los modelos lineales crean buenas explicaciones?

A juzgar por los atributos que constituyen una buena explicación, como se presenta en el capítulo Explicaciones amigables para los humanos, los modelos lineales no crean las mejores explicaciones. Son contrastantes, pero la referencia es una observación donde todas las características numéricas son cero y las características categóricas están en sus categorías basales. Esta suele ser una instancia artificial sin sentido que es poco probable que ocurra en sus datos o realidad. Hay una excepción: Si todas las características numéricas están centradas en la media (característica menos la media de la característica) y todas las características categóricas están codificadas por efecto, la instancia de referencia es el punto de datos donde todas las características toman el valor medio de la característica. Esto también podría ser un punto de datos inexistente, pero al menos podría ser más probable o más significativo. En este caso, los pesos multiplicados por los valores de la característica (efectos de la característica) explican la contribución al resultado predicho en contraste con la “instancia media”. Otro aspecto de una buena explicación es la selectividad, que se puede lograr en modelos lineales usando menos características o entrenando modelos lineales dispersos. Pero por defecto, los modelos lineales no crean explicaciones selectivas. Los modelos lineales crean explicaciones verdaderas, siempre que la ecuación lineal sea un modelo apropiado para la relación entre características y resultados. Cuantas más no linealidades e interacciones haya, menos preciso será el modelo lineal y menos sinceras sus explicaciones. La linealidad hace que las explicaciones sean más generales y más simples. La naturaleza lineal del modelo, creo, es el factor principal por el cual las personas usan modelos lineales para explicar las relaciones.

4.1.7 Modelos lineales dispersos

Los ejemplos de los modelos lineales que he elegido se ven bien y ordenados, ¿no es así? Pero en realidad, es posible que no tengas solo un puñado de características, sino cientos o miles. En esos casos, la interpretabilidad va cuesta abajo. Incluso puedes encontrarte en una situación en la que hay más características que instancias, y no puede ajustarse a un modelo lineal estándar en absoluto. La buena noticia es que hay formas de introducir la reducción (= pocas características) en los modelos lineales.

4.1.7.1 Lasso

Lasso es una forma automática y conveniente de introducir la reducción en el modelo de regresión lineal. Lasso significa “operador de reducción y selección, menor absoluto” y, cuando se aplica en un modelo de regresión lineal, realiza la selección de características y la regularización de los pesos de las características seleccionadas. Consideremos el problema de minimización que optimizan los pesos:

\[min_{\boldsymbol{\beta}}\left(\frac{1}{n}\sum_{i=1}^n(y^{(i)}-x_i^T\boldsymbol{\beta})^2\right)\]

Lasso agrega un término a este problema de optimización.

\[min_{\boldsymbol{\beta}}\left(\frac{1}{n}\sum_{i=1}^n(y^{(i)}-x_{i}^T\boldsymbol{\beta})^2+\lambda||\boldsymbol{\beta}||_1\right)\]

El término \(||\boldsymbol{\beta}||_1\), la norma L1 del vector de características, genera una penalización de los pesos grandes. Cuando se usa la norma L1, muchos de los pesos reciben una estimación de 0 y los otros se reducen. El parámetro lambda (\(\lambda\)) controla la fuerza del efecto de regularización y generalmente se ajusta mediante validación cruzada. Especialmente cuando lambda es grande, muchos pesos se convierten en 0. Los pesos de las características se pueden visualizar en función del término de penalización lambda. El peso de cada característica se representa mediante una curva en la siguiente figura.

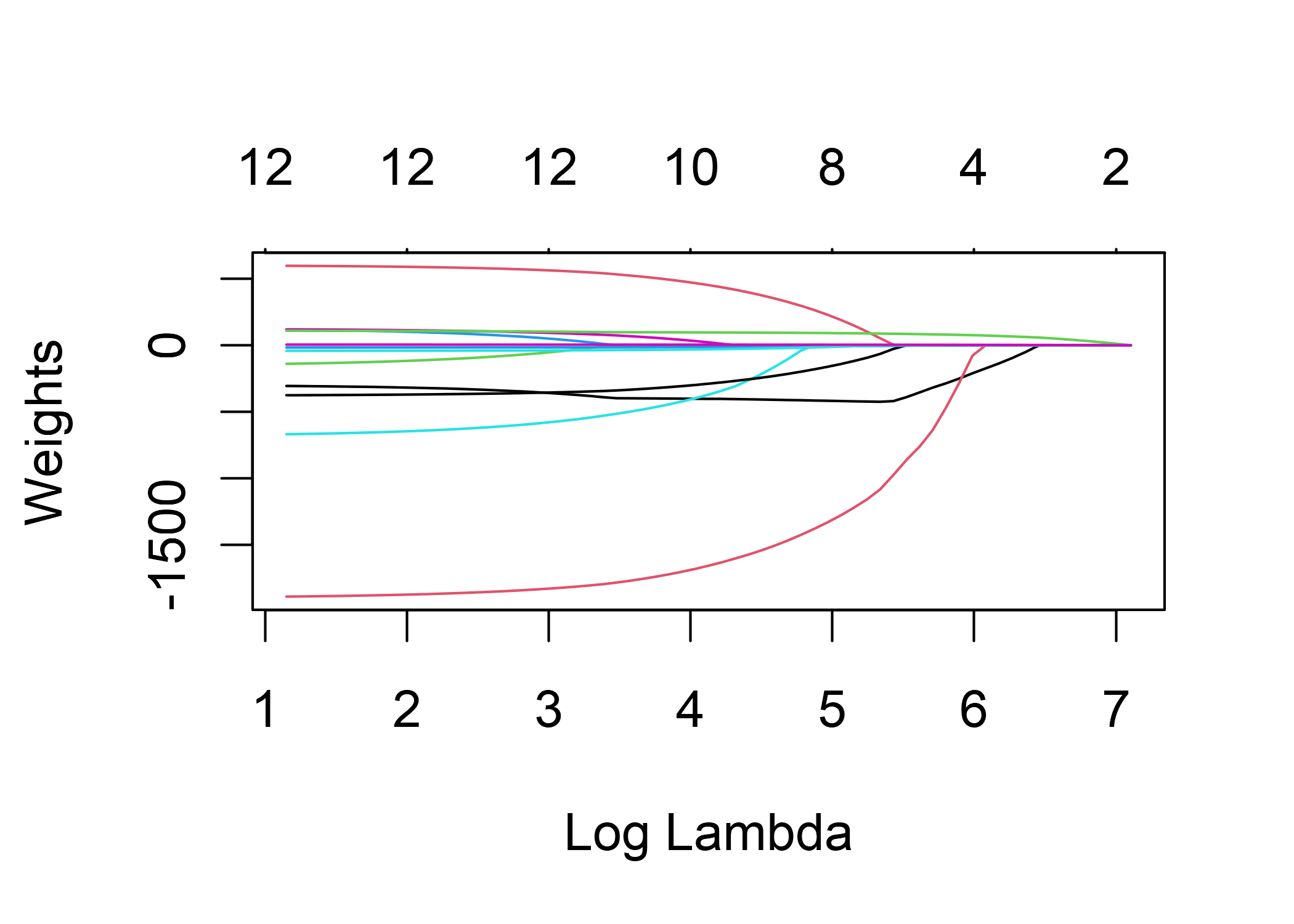
FIGURA 4.4: Incrementando la penalidad de los pesos, cada vez menos características tienen un estimador distinto a cero. A estas curvas también se las llama caminos de regularización.

¿Qué valor deberíamos elegir para lambda? Si ves el término de penalización como un parámetro de ajuste, puedes encontrar la lambda que minimiza el error del modelo con validación cruzada. También puedes considerar lambda como un parámetro para controlar la interpretabilidad del modelo. Cuanto mayor es la penalización, menos características están presentes en el modelo (porque sus pesos son cero) y mejor se puede interpretar el modelo.

Ejemplo con lasso

Vamos a predecir el alquiler de bicicletas con Lasso. Establecemos de antemano la cantidad de características que queremos tener en el modelo. Primero establezcamos el número en 2 características:

	Weight
seasonSPRING	0.00
seasonSUMMER	0.00
seasonFALL	0.00
seasonWINTER	0.00
holidayHOLIDAY	0.00
workingdayWORKING DAY	0.00
weathersitMISTY	0.00
weathersitRAIN/SNOW/STORM	0.00
temp	52.33
hum	0.00
windspeed	0.00
days_since_2011	2.15

Las dos primeras características con pesos distintos de según Lasso son la temperatura (“temp”) y la tendencia temporal (“days_since_2011”).

Ahora, seleccionemos 5 características:

	Weight
seasonSPRING	-389.99
seasonSUMMER	0.00
seasonFALL	0.00
seasonWINTER	0.00
holidayHOLIDAY	0.00
workingdayWORKING DAY	0.00
weathersitMISTY	0.00
weathersitRAIN/SNOW/STORM	-862.27
temp	85.58
hum	-3.04
windspeed	0.00
days_since_2011	3.82

Ten en cuenta que los pesos para “temp” y “days_since_2011” difieren del modelo con dos características. La razón de esto es que al disminuir lambda, incluso las características que ya están “en” el modelo se penalizan menos y pueden obtener un peso absoluto mayor. La interpretación de los pesos de lasso corresponde a la interpretación de los pesos en el modelo de regresión lineal. Solo necesitas prestar atención a si las características están estandarizadas o no, porque esto afecta los pesos. En este ejemplo, el software estandarizó las funciones, pero los pesos se transformaron automáticamente para que coincidan con las escalas de funciones originales.

Otros métodos para la dispersión en modelos lineales

Se puede utilizar un amplio espectro de métodos para reducir el número de características en un modelo lineal.

Métodos de preprocesamiento:

• Funciones seleccionadas manualmente: Siempre puede utilizar el conocimiento experto para seleccionar o descartar algunas funciones. El gran inconveniente es que no se puede automatizar y debes tener acceso a alguien que comprenda los datos.
• Selección univariante: Un ejemplo es el coeficiente de correlación. Solo tiene en cuenta las características que exceden un cierto umbral de correlación entre la característica y el objetivo. La desventaja es que solo considera las características individualmente. Es posible que algunas características no muestren una correlación con el objetivo hasta que el modelo lineal haya tenido en cuenta algunas otras características. Estas no se advertirán con métodos de selección univariantes.

Métodos paso a paso:

• Selección hacia adelante: Ajusta el modelo lineal con una característica. Haz esto con cada característica. Selecciona el modelo que funcione mejor (por ejemplo, el R cuadrado más alto). Ahora, de nuevo, para las características restantes, ajusta diferentes versiones de su modelo agregando cada característica a su mejor modelo actual. Selecciona el que mejor funcione. Continúa hasta que se alcance algún criterio, como el número máximo de características en el modelo.
• Selección hacia atrás: Similar a la selección hacia adelante. Pero en lugar de agregar funciones, comienza con el modelo que contiene todas las funciones y prueba qué variable debes eliminar para obtener el mayor aumento de rendimiento. Repite esto hasta que se alcance algún criterio de detención.

Recomiendo usar Lasso, porque puede ser automatizado, considera todas las características simultáneamente y puede controlarse mediante lambda. También funciona para el modelo de regresión logística para la clasificación.

4.1.8 Ventajas

El modelado de las predicciones como una suma ponderada hace que la forma en la que se produce la predicción sea transparente. Con Lasso podemos asegurarnos de que la cantidad de funciones utilizadas sea pequeña.

Muchas personas usan modelos de regresión lineal. Esto significa que en muchos lugares es aceptado para el modelado predictivo y hacer inferencia. Existe un alto nivel de expertiz y experiencia colectiva, que incluye materiales didácticos sobre modelos de regresión lineal e implementaciones de software. La regresión lineal se puede encontrar en R, Python, Java, Julia, Scala, Javascript, …

Matemáticamente, es sencillo estimar los pesos y tiene una garantía para encontrar pesos óptimos (dado que los datos cumplen todos los supuestos del modelo de regresión lineal).

Junto con los pesos, obtienes intervalos de confianza, pruebas y una sólida teoría estadística. También hay muchas extensiones del modelo de regresión lineal (ver capítulo sobre GLM, GAM y más).

4.1.9 Desventajas

Los modelos de regresión lineal solo pueden representar relaciones lineales, es decir, una suma ponderada de las características de entrada. Cada no linealidad o interacción tiene que ser hecha a mano y entregada explícitamente al modelo como una característica de entrada.

Los modelos lineales a menudo también no son tan buenos con respecto al rendimiento predictivo, porque las relaciones que se pueden aprender son muy restringidas y generalmente simplifican demasiado la realidad, que suele ser más compleja.

La interpretación de un peso puede ser poco intuitiva porque depende de todas las demás características. Una característica con alta correlación positiva con el resultado Y y también con alta correlación positiva con otra característica podría tener un peso negativo en el modelo lineal, porque, dada la otra característica correlacionada, se correlaciona negativamente con Y en el espacio de alta dimensión. Las características completamente correlacionadas hacen que sea incluso imposible encontrar una solución única para la ecuación lineal. Un ejemplo: Tienes un modelo para predecir el valor de una casa, y tienes características como el número de habitaciones y el tamaño de la casa. El tamaño de la casa y el número de habitaciones están altamente correlacionados: cuanto más grande es una casa, más habitaciones tiene. Si tomas ambas características en un modelo lineal, puede suceder que el tamaño de la casa sea el mejor predictor y obtenga un gran peso positivo. El número de habitaciones podría terminar teniendo un peso negativo, ya que, dado que una casa tiene el mismo tamaño, aumentar el número de habitaciones podría hacerla menos valiosa. La ecuación lineal se vuelve menos estable cuando la correlación es demasiado fuerte.

---

16. Friedman, Jerome, Trevor Hastie, and Robert Tibshirani. “The elements of statistical learning”. www.web.stanford.edu/~hastie/ElemStatLearn/ (2009).↩