5.9 Valores de Shapley

Una predicción puede explicarse suponiendo que cada valor de característica de la instancia es un “jugador” en un juego donde la predicción es el pago. Los valores de Shapley, un método de la teoría de juegos de coalición, nos dicen cómo distribuir equitativamente el “pago” entre las características.

5.9.1 Idea general

Supón el siguiente escenario:

Has entrenado un modelo de aprendizaje automático para predecir los precios de los apartamentos. Para un determinado apartamento predice €300,000 y necesitas explicar esta predicción. El apartamento tiene un tamaño de 50 m², está ubicado en el segundo piso, tiene un parque cercano y los gatos están prohibidos:

FIGURA 5.42: El precio previsto para un apartamento de 50 m² en el segundo piso con un parque cercano y prohibición de gatos es de €300,000. Nuestro objetivo es explicar cómo cada uno de estos valores de características contribuyó a la predicción

La predicción promedio para todos los apartamentos es de €310,000. ¿Cuánto ha contribuido cada valor de característica a la predicción en comparación con la predicción promedio?

La respuesta es simple para los modelos de regresión lineal. El efecto de cada característica es el peso de la característica multiplicado por el valor de la característica. Esto solo funciona debido a la linealidad del modelo. Para modelos más complejos, necesitamos una solución diferente. Por ejemplo, LIME sugiere modelos locales para estimar los efectos. Otra solución proviene de la teoría del juego cooperativo: El valor de Shapley, acuñado por Shapley (1953)⁴⁰, es un método para asignar pagos a los jugadores en función de su contribución al pago total. Los jugadores cooperan en una coalición y reciben una cierta ganancia de esta cooperación.

¿Jugadores? ¿Juego? ¿Pagar? ¿Cuál es la conexión con las predicciones e interpretabilidad del aprendizaje automático? El “juego” es la tarea de predicción para una sola instancia del conjunto de datos. La “ganancia” es la predicción real para esta instancia menos la predicción promedio para todas las instancias. Los “jugadores” son las características de la instancia que colaboran para recibir la ganancia (= predecir un cierto valor). En nuestro ejemplo de apartamento, los valores de la característica parque-cerca, gato-prohibido, area-50 y piso-2 trabajaron juntos para lograr la predicción de €300,000. Nuestro objetivo es explicar la diferencia entre la predicción real (€300,000) y la predicción promedio (€310,000): una diferencia de -€10,000.

La respuesta podría ser: El parque-cerca contribuyó con €30,000; area-50 contribuyó con €10.000; piso-2 contribuyó con €0; gato-prohibido contribuyó -€50,000. Las contribuciones suman -€10,000, la predicción final menos el precio promedio previsto del apartamento.

¿Cómo calculamos el valor de Shapley para una característica?

El valor de Shapley es la contribución marginal promedio de un valor de característica en todas las coaliciones posibles. Más claro ahora?

En la siguiente figura, evaluamos la contribución del valor de la característica gato-prohibido cuando se agrega a una coalición de parque-cerca y area-50. Simulamos que solo parque-cerca, gato-prohibido y area-50 están en una coalición extrayendo aleatoriamente otro departamento de los datos y usando su valor para el atributo piso. El valor piso-2 fue reemplazado por el aleatorio dibujado piso-1. Luego predecimos el precio del apartamento con esta combinación (€ 310,000). En un segundo paso, eliminamos gato-prohibido de la coalición reemplazándolo con un valor aleatorio de la característica gato prohibido/permitido del departamento dibujado al azar. En el ejemplo estaba permitido, pero podría ser prohibido nuevamente. Predecimos el precio del apartamento para la coalición de parque cercano y tamaño-50 (€320,000). La contribución de gato prohibido fue de €310,000 - €320,000 = - € 10,000. Esta estimación depende de los valores del apartamento dibujado al azar que sirvió como “donante” para los valores de características de gato y piso. Obtendremos mejores estimaciones si repetimos este paso de muestreo y promediamos las contribuciones.

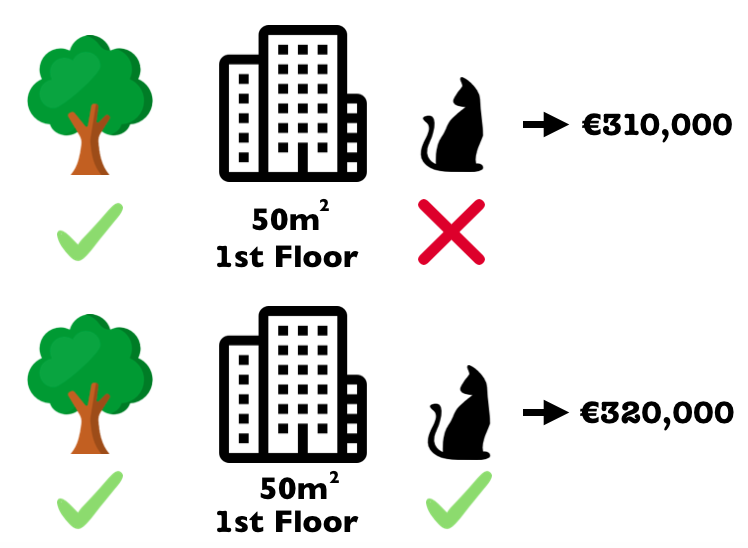
FIGURA 5.43: Una repetición de muestra para estimar la contribución de gato-prohibido a la predicción cuando se agrega a la coalición de ’parque-cercayarea-50`.

Repetimos este cálculo para todas las coaliciones posibles. El valor de Shapley es el promedio de todas las contribuciones marginales a todas las coaliciones posibles. El tiempo de cálculo aumenta exponencialmente con el número de características. Una solución para mantener manejable el tiempo de cálculo es calcular las contribuciones solo para unas pocas muestras de las posibles coaliciones.

La siguiente figura muestra todas las coaliciones de valores de características que se necesitan para determinar el valor de Shapley para gato-prohibido. La primera fila muestra la coalición sin ningún valor de característica. En la imagen, las filas segunda, tercera y cuarta muestran diferentes coaliciones con un tamaño de coalición creciente, separadas por “|”. En general, son posibles las siguientes coaliciones:

• Sin valores de características
• parque-cerca
• area-50
• piso-2
• parque-cerca + area-50
• parque-cerca + piso-2
• area-50 + piso-2
• parque-cerca + area-50 + piso-2

Para cada una de estas coaliciones, calculamos el precio predicho del apartamento con y sin el valor de característica gatos prohibidos y tomamos la diferencia para obtener la contribución marginal. El valor de Shapley es el promedio (ponderado) de las contribuciones marginales. Reemplazamos los valores de características de las características que no están en una coalición con valores de características aleatorias del conjunto de datos del departamento para obtener una predicción del modelo de aprendizaje automático.

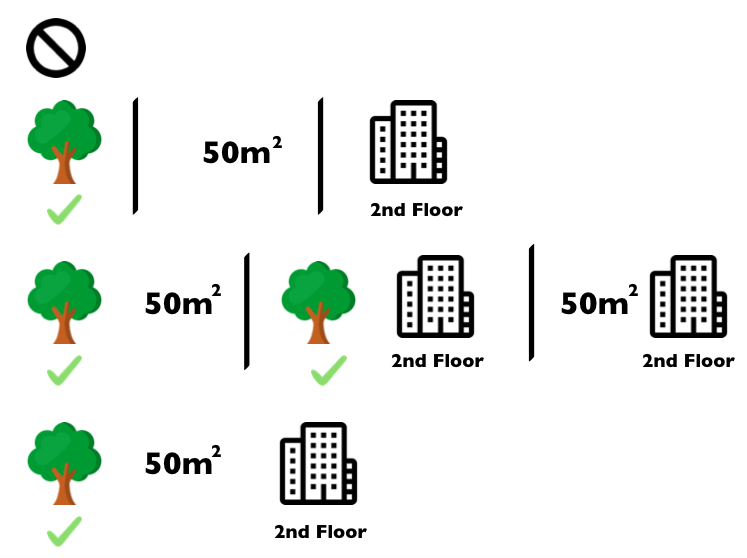
FIGURA 5.44: Las 8 coaliciones necesarias para calcular el valor exacto de Shapley del valor de la característica gatos-prohibidos.

Si estimamos los valores de Shapley para todos los valores de características, obtenemos la distribución completa de la predicción (menos el promedio) entre los valores de características.

5.9.2 Ejemplos e interpretación

La interpretación del valor de Shapley para el valor de característica j es: El valor de la característica j contribuyó \(\phi_j\) a la predicción de esta instancia particular en comparación con la predicción promedio para el conjunto de datos.

El valor de Shapley funciona tanto para la clasificación (si se trata de probabilidades) como para la regresión.

Utilizamos el valor de Shapley para analizar las predicciones de un random forest aleatorio que predice cáncer cervical:

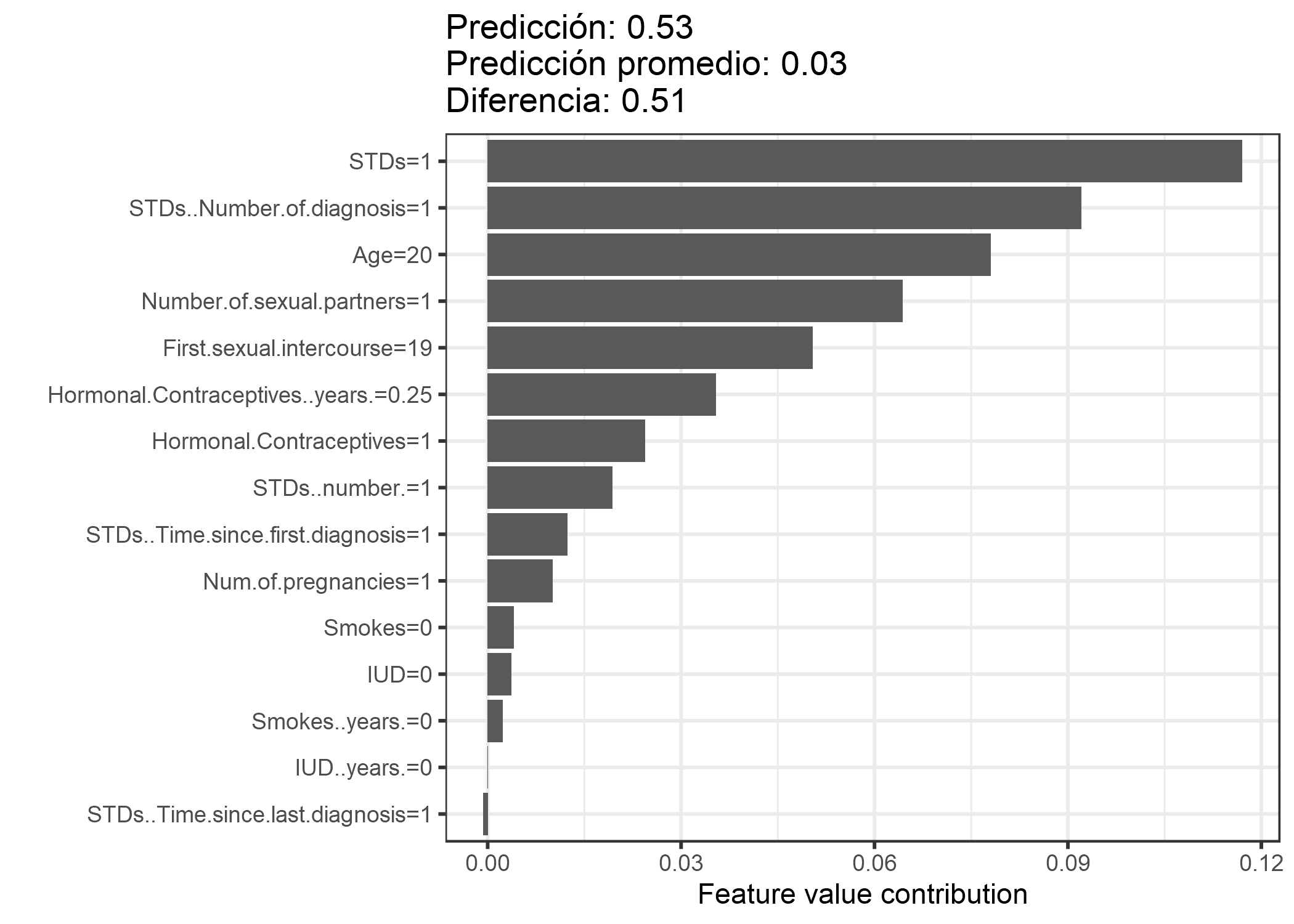
FIGURA 5.45: Valores de Shapley para una mujer en el conjunto de datos de cáncer cervical. Con una predicción de 0.53, la probabilidad de cáncer de esta mujer es 0.51 por encima de la predicción promedio de 0.03. El número de ETS diagnosticadas aumentó la probabilidad más. La suma de las contribuciones produce la diferencia entre la predicción real y la media (0.51)

Para el conjunto de datos de alquiler de bicicletas, también entrenamos un random forest para predecir el número de bicicletas alquiladas por un día, dada la información del clima y el calendario. Las explicaciones creadas para la predicción aleatoria del random forest de un día en particular:

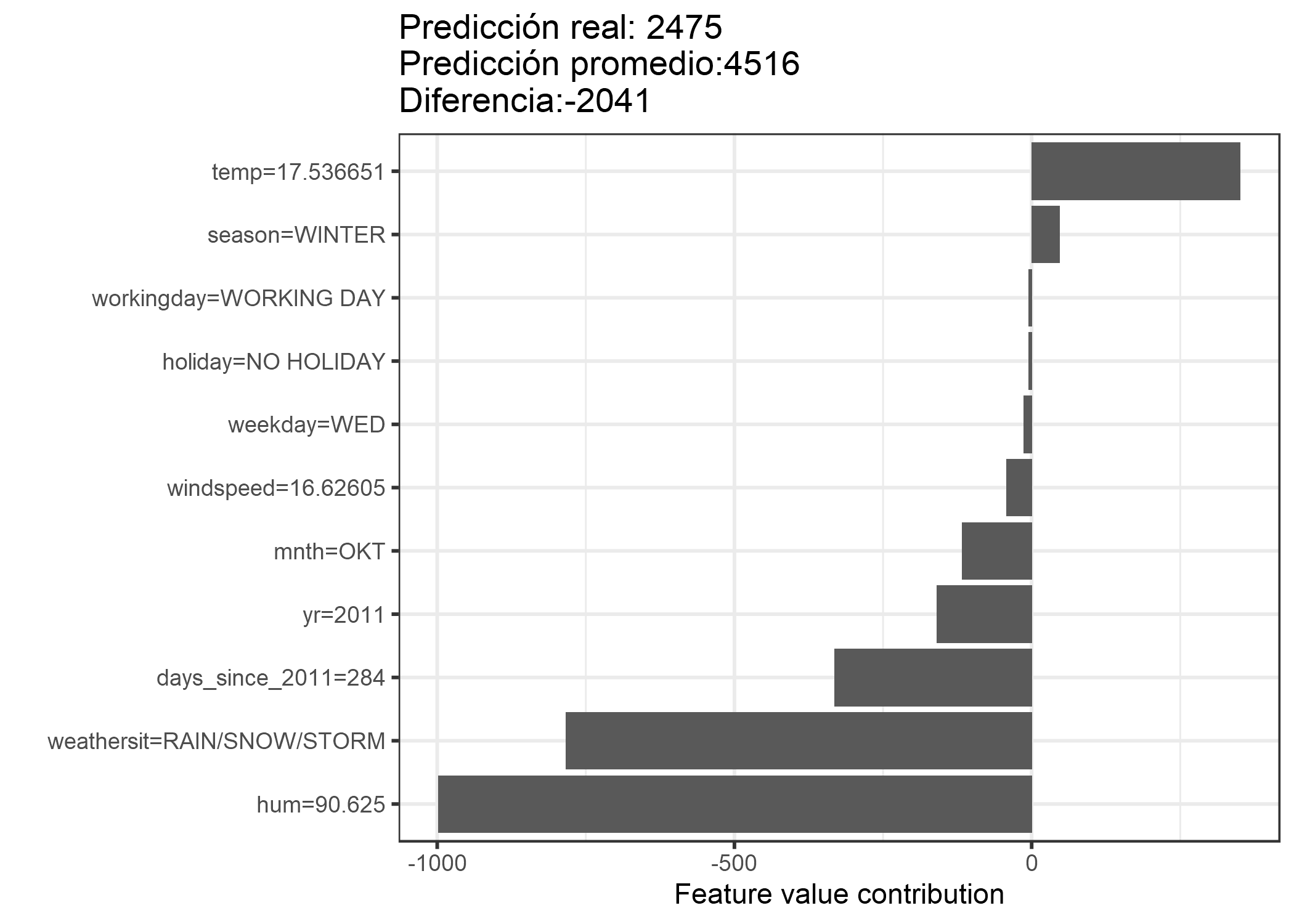
FIGURA 5.46: Valores de Shapley para el día 285. Con un número previsto de 2475 bicicletas alquiladas, este día está -2041 por debajo de la predicción promedio de 4516. la situación climática y la humedad tuvieron las mayores contribuciones negativas. La temperatura en este día tuvo una contribución positiva. La suma de los valores de Shapley produce la diferencia de predicción real y promedio (-2041).

Ten cuidado de interpretar el valor de Shapley correctamente: El valor de Shapley es la contribución promedio de un valor de característica a la predicción en diferentes coaliciones. El valor de Shapley NO es la diferencia en la predicción cuando eliminaríamos la característica del modelo.

5.9.3 El valor de Shapley en detalle

Esta sección profundiza en la definición y el cálculo del valor de Shapley para el lector curioso. Omite esta sección y ve directamente a “Ventajas y desventajas” si no estás interesado en los detalles técnicos.

Estamos interesados en cómo cada característica afecta la predicción de un punto de datos. En un modelo lineal es fácil calcular los efectos individuales. Así es como se ve una predicción de modelo lineal para una instancia de datos:

\[\hat{f}(x)=\beta_0+\beta_{1}x_{1}+\ldots+\beta_{p}x_{p}\]

donde x es la instancia para la que queremos calcular las contribuciones. Cada \(x_j\) es un valor de característica, con j = 1, …, p. \(\beta_j\) es el peso correspondiente al atributo j.

La contribución \(\phi_j\) de la función j-ésima en la predicción \(\hat{f}(x)\) es:

\[\phi_j(\hat{f})=\beta_{j}x_j-E(\beta_{j}X_{j})=\beta_{j}x_j-\beta_{j}E(X_{j})\]

donde \(E(\beta_jX_{j})\) es la estimación del efecto medio para la característica j. La contribución es la diferencia entre el efecto de la característica menos el efecto promedio. ¡Agradable! Ahora sabemos cuánto contribuyó cada característica a la predicción. Si sumamos todas las contribuciones de características para una instancia, el resultado es el siguiente:

\[\begin{align*}\sum_{j=1}^{p}\phi_j(\hat{f})=&\sum_{j=1}^p(\beta_{j}x_j-E(\beta_{j}X_{j}))\\=&(\beta_0+\sum_{j=1}^p\beta_{j}x_j)-(\beta_0+\sum_{j=1}^{p}E(\beta_{j}X_{j}))\\=&\hat{f}(x)-E(\hat{f}(X))\end{align*}\]

Este es el valor predicho para el punto de datos x menos el valor promedio predicho. Las contribuciones de funciones pueden ser negativas.

¿Podemos hacer lo mismo para cualquier tipo de modelo? Sería genial tener esto como una herramienta independiente del modelo. Como generalmente no tenemos pesos similares en otros tipos de modelos, necesitamos una solución diferente.

La ayuda proviene de lugares inesperados: teoría de juegos cooperativos. El valor Shapley es una solución para calcular las contribuciones de características para predicciones individuales para cualquier modelo de aprendizaje automático.

5.9.3.1 El valor de Shapley

El valor de Shapley se define mediante una función de valor val de jugadores en S.

El valor de Shapley de un valor de característica es su contribución al pago, ponderado y sumado sobre todas las combinaciones posibles de valor de característica:

\[\phi_j(val)=\sum_{S\subseteq\{x_{1},\ldots,x_{p}\}\setminus\{x_j\}}\frac{|S|!\left(p-|S|-1\right)!}{p!}\left(val\left(S\cup\{x_j\}\right)-val(S)\right)\]

donde S es un subconjunto de las características utilizadas en el modelo, x es el vector de valores de características de la instancia a explicar y p el número de características. \(val_x(S)\) es la predicción para los valores de características en el conjunto S que están marginados sobre las características que no están incluidas en el conjunto S:

\[val_{x}(S)=\int\hat{f}(x_{1},\ldots,x_{p})d\mathbb{P}_{x\notin{}S}-E_X(\hat{f}(X))\]

Realmente realiza múltiples integraciones para cada característica que no está contenida S. Un ejemplo concreto: El modelo de aprendizaje automático funciona con 4 características x1, x2, x3 y x4 y evaluamos la predicción para la coalición S que consta de valores de características x1 y x3:

\[val_{x}(S)=val_{x}(\{x_{1},x_{3}\})=\int_{\mathbb{R}}\int_{\mathbb{R}}\hat{f}(x_{1},X_{2},x_{3},X_{4})d\mathbb{P}_{X_2X_4}-E_X(\hat{f}(X))\]

¡Esto se parece a las contribuciones de características en el modelo lineal!

No lo confudas con los muchos usos de la palabra “valor”: El valor de la característica es el valor numérico o categórico de una característica e instancia; el valor de Shapley es la contribución de la característica a la predicción; la función de valor es la función de pago para coaliciones de jugadores (valores de características).

El valor de Shapley es el único método de atribución que satisface las propiedades Eficiencia, Simetría, Dummies y Aditividad, que juntas pueden considerarse una definición de pago justo.

Eficiencia
Las contribuciones de características deben sumarse a la diferencia de predicción para x y el promedio.

\[\sum\nolimits_{j=1}^p\phi_j=\hat{f}(x)-E_X(\hat{f}(X))\]

Simetría
Las contribuciones de dos valores de características j y k deberían ser las mismas si contribuyen igualmente a todas las coaliciones posibles. Si

\[val(S\cup\{x_j\})=val(S\cup\{x_k\})\]

para todos

\[S\subseteq\{x_{1},\ldots,x_{p}\}\setminus\{x_j,x_k\}\]

luego

\[\phi_j=\phi_{k}\]

Dummies
Una característica j que no cambia el valor predicho, independientemente de a qué coalición de valores de característica se agregue, debe tener un valor Shapley de 0. Si

\[val(S\cup\{x_j\})=val(S)\]

para todos

\[S\subseteq\{x_{1},\ldots,x_{p}\}\]

luego

\[\phi_j=0\]

Aditividad
Para un juego con pagos combinados val+val⁺, los valores de Shapley respectivos son los siguientes:

\[\phi_j+\phi_j^{+}\]

Supongamos que entrenaste un random forest, lo que significa que la predicción es un promedio de muchos árboles de decisión. La propiedad Aditividad garantiza que para un valor de característica, puedes calcular el valor de Shapley para cada árbol individualmente, promediarlos y obtener el valor de Shapley para el valor de característica para el random forest.

5.9.3.2 Intuición

Una forma intuitiva de comprender el valor de Shapley es la siguiente ilustración: Los valores de las características ingresan a una habitación en orden aleatorio. Todos los valores de características en la sala participan en el juego (= contribuyen a la predicción). El valor de Shapley de un valor de característica es el cambio promedio en la predicción que la coalición que ya está en la sala recibe cuando el valor de característica se une a ellos.

5.9.3.3 Estimación del valor de Shapley

Todas las coaliciones (conjuntos) posibles de valores de características deben evaluarse con y sin la característica j-ésima para calcular el valor exacto de Shapley. Para más de unas pocas características, la solución exacta a este problema se vuelve problemática ya que el número de coaliciones posibles aumenta exponencialmente a medida que se agregan más características. Strumbelj et al. (2014)⁴¹ proponen una aproximación con el muestreo de Monte-Carlo:

\[\hat{\phi}_{j}=\frac{1}{M}\sum_{m=1}^M\left(\hat{f}(x^{m}_{+j})-\hat{f}(x^{m}_{-j})\right)\]

donde \(\hat{f}(x^{m}_{+j})\) es la predicción para x, pero con un número aleatorio de valores de características reemplazados por valores de características de un punto de datos aleatorio z, excepto el valor respectivo de la característica j. El vector x \(x^{m}_{-j}\) es casi idéntico a \(x^{m}_{+j}\), pero el valor \(x_j^{m}\) también se toma de la muestra z. Cada una de estas M nuevas instancias es una especie de “Frankenstein” ensamblado a partir de dos instancias.

Estimación aproximada de Shapley para el valor de una sola característica:

• Salida: valor de Shapley para el valor de la característica j-ésima
• Requerido: Número de iteraciones M, instancia de interés x, índice de características j, matriz de datos X y modelo de aprendizaje automático f   - Para todos m = 1, …, M:
  • Dibuja una instancia aleatoria z de la matriz de datos X
  • Elige una permutación aleatoria de los valores de la característica
  • Instancia de pedido x: \(x_o=(x_{(1)},\ldots,x_{(j)},\ldots,x_{(p)})\)
  • Instancia de pedido z: \(z_o=(z_{(1)},\ldots,z_{(j)},\ldots,z_{(p)})\)
  • Construye dos nuevas instancias
    • Con la función j: \(x_{+j}=(x_{(1)},\ldots,x_{(j-1)},x_{(j)},z_{(j+1)},\ldots,z_{(p)})\)
    • Sin la característica j: \(x_{-j}=(x_{(1)},\ldots,x_{(j-1)},z_{(j)},z_{(j+1)},\ldots,z_{(p)})\)
  • Calcular contribución marginal: \(\phi_j^{m}=\hat{f}(x_{+j})-\hat{f}(x_{-j})\)
• Calcular el valor de Shapley como el promedio: \(\phi_j(x)=\frac{1}{M}\sum_{m=1}^M\phi_j^{m}\)

Primero, selecciona una instancia de interés x, una característica j y el número de iteraciones M. Para cada iteración, se selecciona una instancia aleatoria z de los datos y se genera un orden aleatorio de las características. Se crean dos nuevas instancias combinando valores de la instancia de interés x y la muestra z. La primera instancia \(x_{+j}\) es la instancia de interés, pero todos los valores en el orden anterior e incluido el valor de la característica j se reemplazan por los valores de la característica de la muestra z. La segunda instancia \(x_{-j}\) es similar, pero tiene todos los valores en el orden anterior, pero excluye la característica j reemplazada por los valores de la característica j de la muestra z. Se calcula la diferencia en la predicción de caja negra:

\[\phi_j^{m}=\hat{f}(x^m_{+j})-\hat{f}(x^m_{-j})\]

Todas estas diferencias se promedian y dan como resultado:

\[\phi_j(x)=\frac{1}{M}\sum_{m=1}^M\phi_j^{m}\]

El promedio pesa implícitamente las muestras por la distribución de probabilidad de X.

El procedimiento debe repetirse para cada una de las características para obtener todos los valores de Shapley.

5.9.4 Ventajas

La diferencia entre la predicción y la predicción promedio está distribuida de manera justa entre los valores de característica de la instancia: la propiedad de eficiencia de los valores de Shapley. Esta propiedad distingue el valor Shapley de otros métodos como LIME. LIME no garantiza que la predicción se distribuya equitativamente entre las características. El valor de Shapley podría ser el único método para entregar una explicación completa. En situaciones donde la ley requiere explicabilidad, como el “derecho a explicaciones” de la UE, el valor de Shapley podría ser el único método legalmente compatible, porque se basa en una teoría sólida y distribuye los efectos de manera justa. No soy abogado, así que esto refleja solo mi intuición sobre los requisitos.

El valor de Shapley permite explicaciones contrastantes. En lugar de comparar una predicción con la predicción promedio de todo el conjunto de datos, puedes compararla con un subconjunto o incluso con un único punto de datos. Este contraste también es algo que los modelos locales como LIME no tienen.

El valor de Shapley es el único método de explicación con una teoría sólida. Los axiomas (eficiencia, simetría, dummies, aditividad) dan a la explicación una base razonable. Métodos como LIME suponen un comportamiento lineal del modelo de aprendizaje automático a nivel local, pero no hay una teoría de por qué esto debería funcionar.

Es alucinante explicar una predicción como un juego jugado por los valores de las características.

5.9.5 Desventajas

El valor de Shapley requiere mucho tiempo de cómputo. En el 99.9% de los problemas del mundo real, solo la solución aproximada es factible. Un cálculo exacto del valor de Shapley es computacionalmente costoso porque hay 2^k posibles coaliciones de los valores de la característica y la “ausencia” de una característica tiene que ser simulada dibujando instancias aleatorias, lo que aumenta la varianza para la estimación de Shapley estimación de valores. El número exponencial de las coaliciones se trata muestreando coaliciones y limitando el número de iteraciones M. La disminución de M reduce el tiempo de cálculo, pero aumenta la varianza del valor de Shapley. No hay una buena regla general para el número de iteraciones M. M debe ser lo suficientemente grande como para estimar con precisión los valores de Shapley, pero lo suficientemente pequeño como para completar el cálculo en un tiempo razonable. Debería ser posible elegir M en función de los límites de Chernoff, pero no he visto ningún documento sobre cómo hacer esto para los valores de Shapley para las predicciones de aprendizaje automático.

El valor de Shapley puede malinterpretarse. El valor de Shapley de un valor de característica no es la diferencia del valor pronosticado después de eliminar la característica del entrenamiento del modelo. La interpretación del valor de Shapley es: Dado el conjunto actual de valores de características, la contribución de un valor de característica a la diferencia entre la predicción real y la predicción media es el valor estimado de Shapley.

El valor de Shapley es el método de explicación incorrecto si busca explicaciones dispersas (explicaciones que contienen pocas características). Las explicaciones creadas con el método de valor Shapley siempre usan todas las características. Los humanos prefieren explicaciones selectivas, como las producidas por LIME. LIME podría ser la mejor opción para las explicaciones con las que los laicos tienen que lidiar. Otra solución es SHAP presentada por Lundberg y Lee (2016)⁴², que se basa en el valor de Shapley, pero también puede proporcionar explicaciones con pocas características.

El valor de Shapley devuelve un valor simple por característica, pero sin modelo de predicción como LIME. Esto significa que no se puede usar para hacer declaraciones sobre cambios en la predicción de cambios en la entrada, como: “Si ganara 300 euros más al año, mi puntaje de crédito aumentaría en 5 puntos”.

Otra desventaja es que necesitas acceso a los datos si deseas calcular el valor de Shapley para una nueva instancia de datos. No es suficiente acceder a la función de predicción porque necesitas los datos para reemplazar partes de la instancia de interés con valores de instancias de datos extraídos al azar. Esto solo se puede evitar si puedes crear instancias de datos que se vean como instancias de datos reales pero que no sean instancias reales a partir de los datos de entrenamiento.

Al igual que muchos otros métodos de interpretación basados en permutación, el método del valor de Shapley sufre de inclusión de instancias de datos poco realistas cuando las características están correlacionadas. Para simular que falta un valor de característica en una coalición, marginalizamos la característica. Esto se logra mediante el muestreo de valores de la distribución marginal de la entidad. Esto está bien siempre que las características sean independientes. Cuando las características dependen, entonces podríamos probar valores de características que no tienen sentido para esta instancia. Pero los usaríamos para calcular el valor Shapley de la entidad. Que yo sepa, no hay investigación sobre lo que eso significa para los valores de Shapley, ni una sugerencia sobre cómo solucionarlo. Una solución podría ser permutar características correlacionadas juntas y obtener un valor mutuo de Shapley para ellas. O el procedimiento de muestreo podría tener que ajustarse para tener en cuenta la dependencia de las características.

5.9.6 Software y alternativas

Los valores de Shapley se implementan en el paquete iml R.

SHAP, un método de estimación alternativo para los valores de Shapley, se presenta en el próximo capítulo.

Otro enfoque se llama breakDown, que se implementa en el paquete breakDown. BreakDown también muestra las contribuciones de cada característica a la predicción, pero las calcula paso a paso. Reutilicemos la analogía del juego: Comenzamos con un equipo vacío, agregamos el valor de la característica que contribuiría más a la predicción e iteramos hasta que se agreguen todos los valores de la característica. La contribución de cada valor de característica depende de los valores de característica respectivos que ya están en el “equipo”, que es el gran inconveniente del método breakDown. Es más rápido que el método de valor Shapley, y para modelos sin interacciones, los resultados son los mismos.

---

40. Shapley, Lloyd S. “A value for n-person games.” Contributions to the Theory of Games 2.28 (1953): 307-317.↩

41. Štrumbelj, Erik, and Igor Kononenko. “Explaining prediction models and individual predictions with feature contributions.” Knowledge and information systems 41.3 (2014): 647-665.↩

42. Lundberg, Scott M., and Su-In Lee. “A unified approach to interpreting model predictions.” Advances in Neural Information Processing Systems. 2017.↩