5.3 Gráfico de efectos locales acumulados (ALE)

Los efectos locales acumulados ³⁰ describen cómo las características influyen en la predicción de un modelo de aprendizaje automático en promedio. Los gráficos ALE son una alternativa más rápida e imparcial a los gráficos de dependencia parcial (PDP).

Recomiendo leer primero el capítulo sobre gráficas de dependencia parcial, ya que son más fáciles de entender y ambos métodos comparten el mismo objetivo: Ambos describen cómo una característica afecta la predicción en promedio. En la siguiente sección, quiero convencerte de que los gráficos de dependencia parcial tienen un problema grave cuando las características están correlacionadas.

5.3.1 Motivación e intuición

Si las características de un modelo de aprendizaje automático están correlacionadas, no se puede confiar en el diagrama de dependencia parcial. El cálculo de una gráfica de dependencia parcial para una característica que está fuertemente correlacionada con otras características implica promedios de instancias de datos artificiales que son poco probables en la realidad. Esto puede sesgar en gran medida el efecto de función estimado. Imagina calcular gráficos de dependencia parcial para un modelo de aprendizaje automático que predice el valor de una casa en función del número de habitaciones y el tamaño de la superficie habitable. Estamos interesados en el efecto del área habitable en el valor predicho. Como recordatorio, la receta para los gráficos de dependencia parcial es: 1) Seleccionar variable. 2) Definir cuadrícula. 3) Por valor de cuadrícula: a) Reemplazar la característica con el valor de cuadrícula y b) predicciones promedio. 4) Dibujar curva. Para el cálculo del primer valor de cuadrícula del PDP, digamos 30 m^2, reemplazamos el área habitable para todas instancias por 30 m^2, incluso para casas con 10 habitaciones. A mí me parece una casa muy inusual. El diagrama de dependencia parcial incluye estas casas poco realistas en la estimación del efecto característico y pretende que todo está bien. La siguiente figura ilustra dos características correlacionadas y cómo resulta que el método de diagrama de dependencia parcial promedia las predicciones de instancias poco probables.

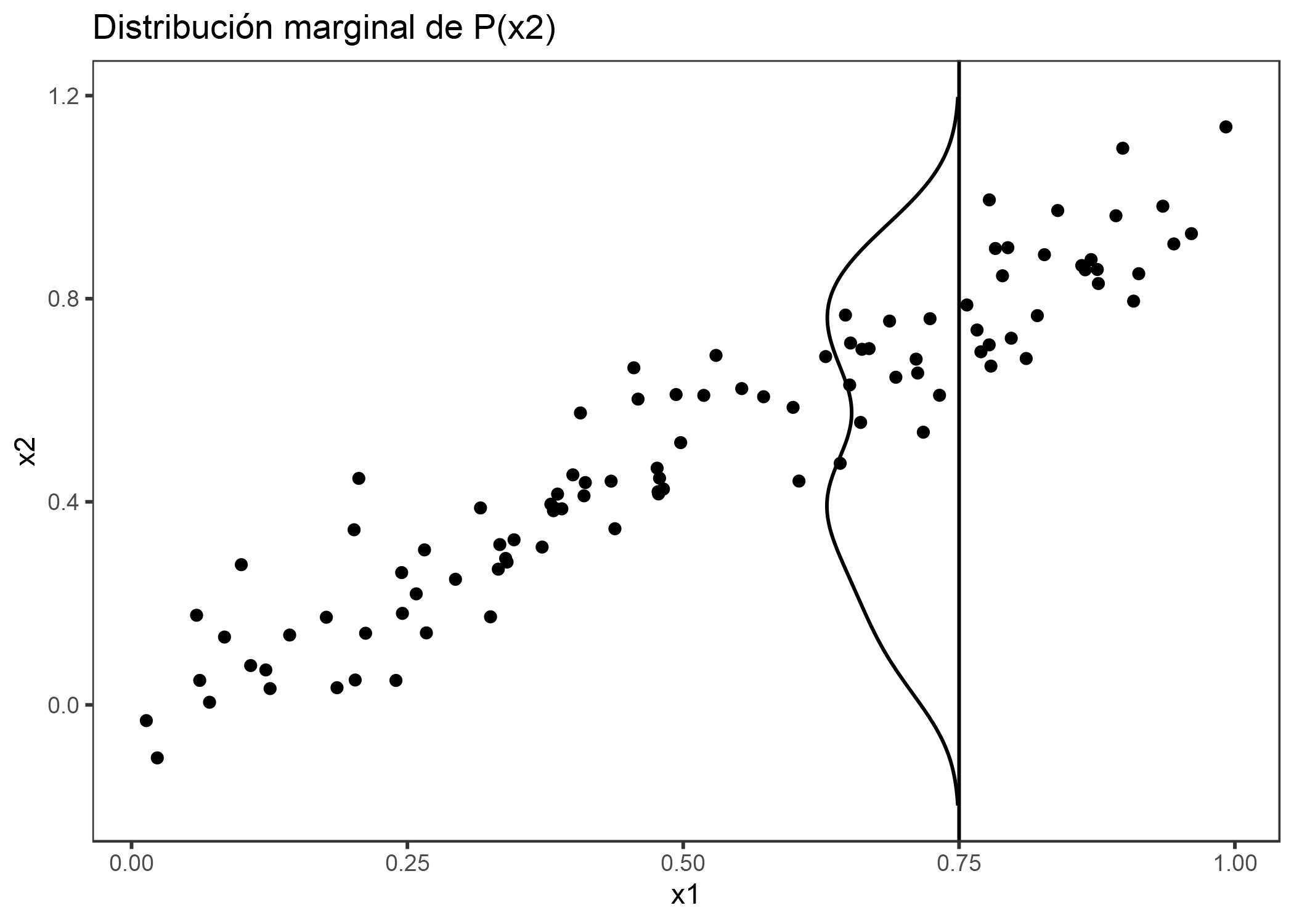
FIGURA 5.10: Características fuertemente correlacionadas x1 y x2. Para calcular el efecto de función de x1 en 0.75, el PDP reemplaza x1 de todas las instancias con 0.75, suponiendo falsamente que la distribución de x2 en x1 = 0.75 es lo mismo que la distribución marginal de x2 (línea vertical). Esto da como resultado combinaciones poco probables de x1 y x2 (p. Ej. X2 = 0.2 en x1 = 0.75), que el PDP usa para calcular el efecto promedio.

¿Qué podemos hacer para obtener una estimación del efecto de la característica que respete la correlación de las características? Podríamos promediar sobre la distribución condicional de la característica, es decir, con un valor de cuadrícula de x1, promediamos las predicciones de instancias con un valor de x1 similar. La solución para calcular los efectos de entidad usando la distribución condicional se llama Gráficos marginales o M-Plots (nombre confuso, ya que se basan en la distribución condicional, no marginal). Espera, ¿no te prometí que hablaría de los gráficos ALE? Los M-Plots no son la solución que estamos buscando. ¿Por qué los M-Plots no resuelven nuestro problema? Si promediamos las predicciones de todas las casas de aproximadamente 30 m^2, estimamos el efecto combinado del área habitable y del número de habitaciones, debido a su correlación. Suponga que la sala de estar no tiene efecto sobre el valor predicho de una casa, solo el número de habitaciones lo tiene. El diagrama M aún mostraría que el tamaño del área de vida aumenta el valor predicho, ya que el número de habitaciones aumenta con el área de vida. La siguiente gráfica muestra para dos características correlacionadas cómo funcionan los M-Plots.

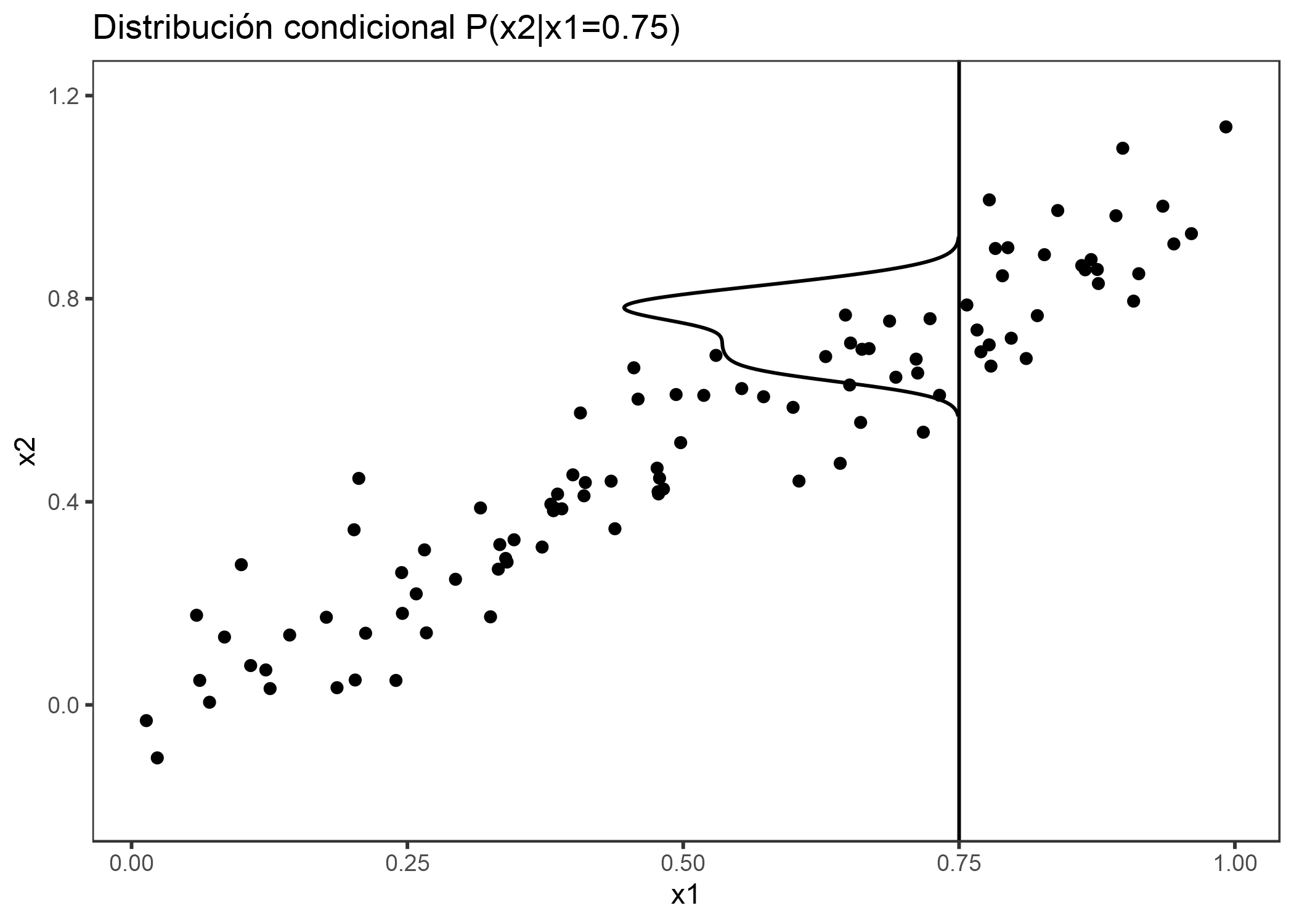
FIGURA 5.11: Características fuertemente correlacionadas x1 y x2. M-Plots promedio sobre la distribución condicional. Aquí la distribución condicional de x2 en x1 = 0.75. El promedio de las predicciones locales lleva a mezclar los efectos de ambas características

Los Gráficos M evitan promedios de instancias de datos poco probables, pero mezclan el efecto de una característica con los efectos de todas las características correlacionadas. Las gráficas ALE resuelven este problema calculando, también en función de la distribución condicional de las características, diferencias en las predicciones en lugar de promedios. Para el efecto del área habitable a 30 m^2, el método ALE usa todas las casas con aproximadamente 30 m^2, obtiene las predicciones del modelo que fingen que estas casas fueron de 31 m^2 menos la predicción que finge que eran 29 m^2. Esto nos da el efecto puro de la sala de estar y no está mezclando el efecto con los efectos de características correlacionadas. El uso de diferencias bloquea el efecto de otras características. El siguiente gráfico proporciona una intuición de cómo se calculan los gráficos ALE.

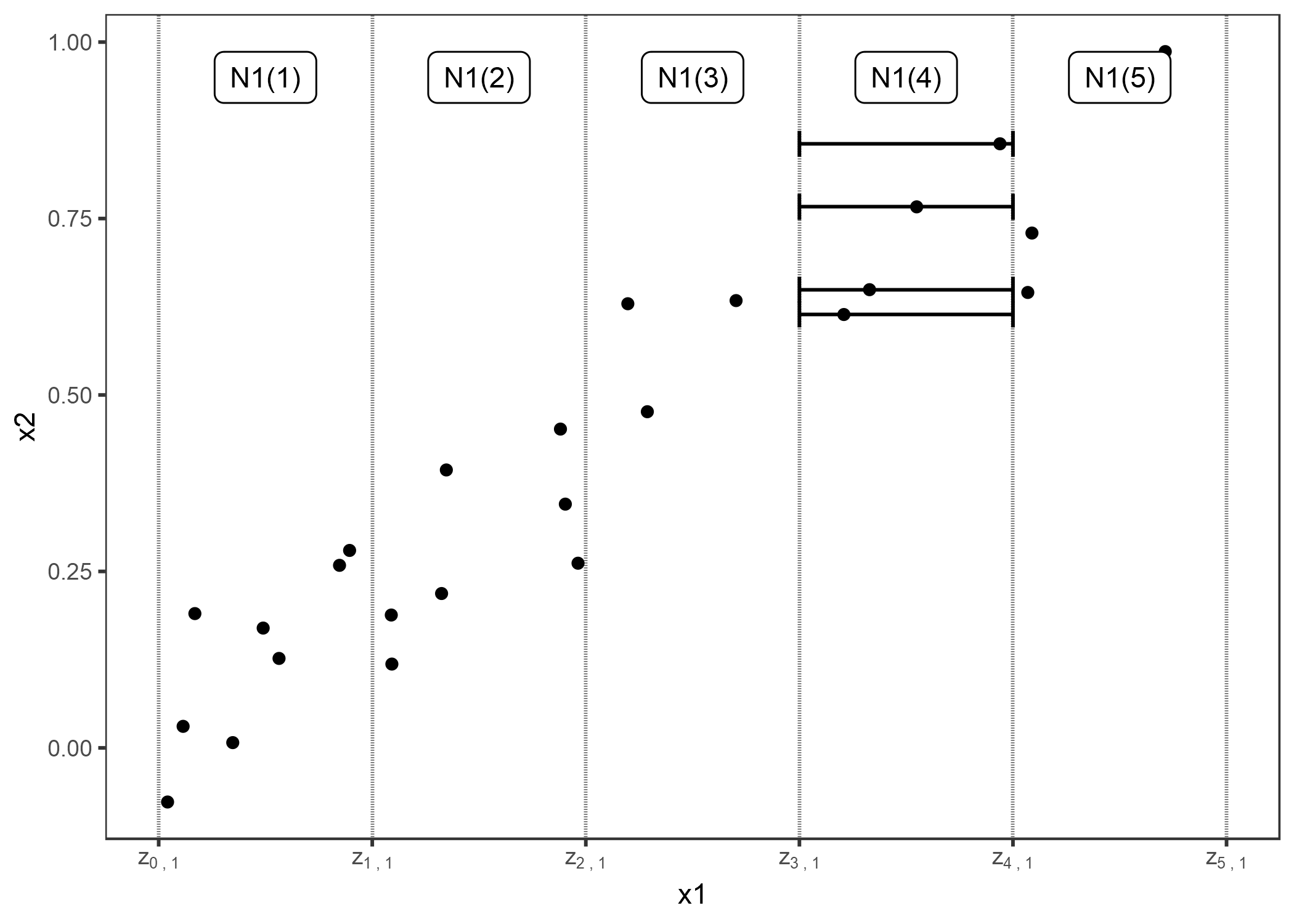
FIGURA 5.12: Cálculo de ALE para la característica x1, que se correlaciona con x2. Primero, dividimos la característica en intervalos (líneas verticales). Para las instancias de datos (puntos) en un intervalo, calculamos la diferencia en la predicción cuando reemplazamos la entidad con el límite superior e inferior del intervalo (líneas horizontales). Estas diferencias se acumulan y centran posteriormente, lo que da como resultado la curva ALE.

Para resumir cómo cada tipo de gráfico (PDP, M, ALE) calcula el efecto de una característica en un determinado valor de cuadrícula v:

Gráficos de dependencia parcial: “Permíteme mostrarte lo que el modelo predice en promedio cuando cada instancia de datos tiene el valor v para esa característica. Ignoro si el valor v tiene sentido para todas las instancias de datos”.

M-Plots: “Déjame mostrarte lo que el modelo predice en promedio para instancias de datos que tienen valores cercanos a v para esa característica. El efecto podría deberse a esa característica, pero también a características correlacionadas”.

Gráfica ALE: “Permíteme mostrarte cómo cambian las predicciones del modelo en una pequeña ‘ventana’ de la función alrededor de v para instancias de datos en esa ventana”.

5.3.2 Teoría

¿Cómo difieren matemáticamente las gráficas PD, M y ALE? Es común a los tres métodos que reducen la compleja función de predicción f a una función que depende de solo una (o dos) características. Los tres métodos reducen la función promediando los efectos de las otras características, pero difieren en si se calculan los promedios de las predicciones o las diferencias en las predicciones y si el promedio se realiza sobre la distribución marginal o condicional.

Los gráficos de dependencia parcial promedian las predicciones sobre la distribución marginal.

\[\begin{align*}\hat{f}_{x_S,PDP}(x_S)&=E_{X_C}\left[\hat{f}(x_S,X_C)\right]\\&=\int_{x_C}\hat{f}(x_S,x_C)\mathbb{P}(x_C)d{}x_C\end{align*}\]

Este es el valor de la función de predicción f, en los valores de función \(x_S\), promediado sobre todas las funciones en \(x_C\). Promedio significa calcular la expectativa marginal E sobre las características del conjunto C, que es la integral sobre las predicciones ponderadas por la distribución de probabilidad. Suena elegante, pero para calcular el valor esperado sobre la distribución marginal, simplemente tomamos todas nuestras instancias de datos, les obligamos a tener un cierto valor de cuadrícula para las características en el conjunto S y promediamos las predicciones para este conjunto de datos manipulados. Este procedimiento asegura que promediamos la distribución marginal de las características.

Las Gráficas M promedian las predicciones sobre la distribución condicional.

\[\begin{align*}\hat{f}_{x_S,M}(x_S)&=E_{X_C|X_S}\left[\hat{f}(X_S,X_C)|X_S=x_s\right]\\&=\int_{x_C}\hat{f}(x_S,x_C)\mathbb{P}(x_C|x_S)d{}x_C\end{align*}\]

Lo único que cambia en comparación con los PDP es que promediamos las predicciones condicionales a cada valor de cuadrícula de la característica de interés, en lugar de asumir la distribución marginal en cada valor de cuadrícula. En la práctica, esto significa que tenemos que definir un vecindario, por ejemplo, para el cálculo del efecto de 30 m^2 en el valor predicho de la casa, podríamos promediar las predicciones de todas las casas entre 28 y 32 m^2.

Las gráficas ALE promedian los cambios en las predicciones y las acumulan sobre la cuadrícula (más sobre el cálculo más adelante).

\[\begin{align*}\hat{f}_{x_S,ALE}(x_S)=&\int_{z_{0,1}}^{x_S}E_{X_C|X_S}\left[\hat{f}^S(X_s,X_c)|X_S=z_S\right]dz_S-\text{constant}\\=&\int_{z_{0,1}}^{x_S}\int_{x_C}\hat{f}^S(z_s,x_c)\mathbb{P}(x_C|z_S)d{}x_C{}dz_S-\text{constant}\end{align*}\]

La fórmula revela tres diferencias con los M-Plots. Primero, promediamos los cambios de las predicciones, no las predicciones en sí. El cambio se define como el gradiente (pero más tarde, para el cálculo real, reemplazado por las diferencias en las predicciones durante un intervalo).

\[\hat{f}^S(x_s,x_c)=\frac{\delta\hat{f}(x_S,x_C)}{\delta{}x_S}\]

La segunda diferencia es la integral adicional sobre z. Acumulamos los gradientes locales sobre el rango de características en el conjunto S, lo que nos da el efecto de la característica en la predicción. Para el cálculo real, las z se reemplazan por una cuadrícula de intervalos sobre los cuales calculamos los cambios en la predicción. En lugar de promediar directamente las predicciones, el método ALE calcula las diferencias de predicción condicionales a las características S e integra la derivada sobre las características S para estimar el efecto. Bueno, eso suena estúpido. La derivación y la integración generalmente se cancelan entre sí, como restar primero y luego sumar el mismo número. ¿Por qué tiene sentido aquí? La derivada (o diferencia de intervalo) aísla el efecto de la característica de interés y bloquea el efecto de las características correlacionadas.

La tercera diferencia de los gráficos ALE con los gráficos M es que restamos una constante de los resultados. Este paso centra el gráfico ALE para que el efecto promedio sobre los datos sea cero.

Queda un problema: No todos los modelos vienen con un gradiente, por ejemplo, el random forest no tiene gradiente. Pero como verás, el cálculo real funciona sin gradientes y utiliza intervalos. Profundicemos un poco más en la estimación de las gráficas ALE.

5.3.3 Estimación

Primero describiré cómo se estiman las gráficas ALE para una sola característica numérica, luego para dos características numéricas y para una sola característica categórica. Para estimar los efectos locales, dividimos la característica en muchos intervalos y calculamos las diferencias en las predicciones. Este procedimiento aproxima los gradientes y también funciona para modelos sin gradientes.

Primero estimamos el efecto no centrado:

\[\hat{\tilde{f}}_{j,ALE}(x)=\sum_{k=1}^{k_j(x)}\frac{1}{n_j(k)}\sum_{i:x_{j}^{(i)}\in{}N_j(k)}\left[f(z_{k,j},x^{(i)}_{\setminus{}j})-f(z_{k-1,j},x^{(i)}_{\setminus{}j})\right]\]

Analicemos esta fórmula, comenzando por el lado derecho. El nombre Efectos locales acumulados refleja muy bien todos los componentes individuales de esta fórmula. En esencia, el método ALE calcula las diferencias en las predicciones, por lo que reemplazamos la característica de interés con valores de cuadrícula z. La diferencia en la predicción es el Efecto que tiene la característica para una instancia individual en un intervalo determinado. La suma de la derecha suma los efectos de todas las instancias dentro de un intervalo que aparece en la fórmula como vecindario \(N_j(k)\). Dividimos esta suma por el número de instancias en este intervalo para obtener la diferencia promedio de las predicciones para este intervalo. Este promedio en el intervalo está cubierto por el término Local en el nombre ALE. El símbolo de suma izquierda significa que acumulamos los efectos promedio en todos los intervalos. El ALE (no centrado) de un valor de característica que se encuentra, por ejemplo, en el tercer intervalo es la suma de los efectos del primer, segundo y tercer intervalo. La palabra Acumulado en ALE refleja esto.

Este efecto está centrado para que el efecto medio sea cero.

\[\hat{\tilde{f}}_{j,ALE}(x)=\sum_{k=1}^{k_j(x)}\frac{1}{n_j(k)}\sum_{i:x_{j}^{(i)}\in{}N_j(k)}\left[f(z_{k,j},x^{(i)}_{\setminus{}j})-f(z_{k-1,j},x^{(i)}_{\setminus{}j})\right]\]

El valor de la ALE puede interpretarse como el efecto principal de la característica en un cierto valor en comparación con la predicción promedio de los datos. Por ejemplo, una estimación de ALE de -2 en \(x_j = 3\) significa que cuando la característica j-ésima tiene el valor 3, entonces la predicción es menor en 2 en comparación con la predicción promedio.

Los cuantiles de la distribución de la característica se utilizan como la cuadrícula que define los intervalos. El uso de los cuantiles garantiza que haya el mismo número de instancias de datos en cada uno de los intervalos. Los cuantiles tienen la desventaja de que los intervalos pueden tener longitudes muy diferentes. Esto puede conducir a algunos gráficos ALE extraños si la característica de interés está muy sesgada, por ejemplo, muchos valores bajos y solo unos pocos valores muy altos.

Gráficos ALE para la interacción de dos características

Las gráficas ALE también pueden mostrar el efecto de interacción de dos características. Los principios de cálculo son los mismos que para una entidad única, pero trabajamos con celdas rectangulares en lugar de intervalos, porque tenemos que acumular los efectos en dos dimensiones. Además de ajustar el efecto medio general, también ajustamos los efectos principales de ambas características. Esto significa que ALE para dos características estima el efecto de segundo orden, que no incluye los efectos principales de las características. En otras palabras, ALE para dos características solo muestra el efecto de interacción adicional de las dos características. Le ahorro las fórmulas para gráficos 2D ALE porque son largas y desagradables de leer. Si estás interesado en el cálculo, te remito al artículo, fórmulas (13) - (16). Confiaré en las visualizaciones para desarrollar la intuición sobre el cálculo de ALE de segundo orden.

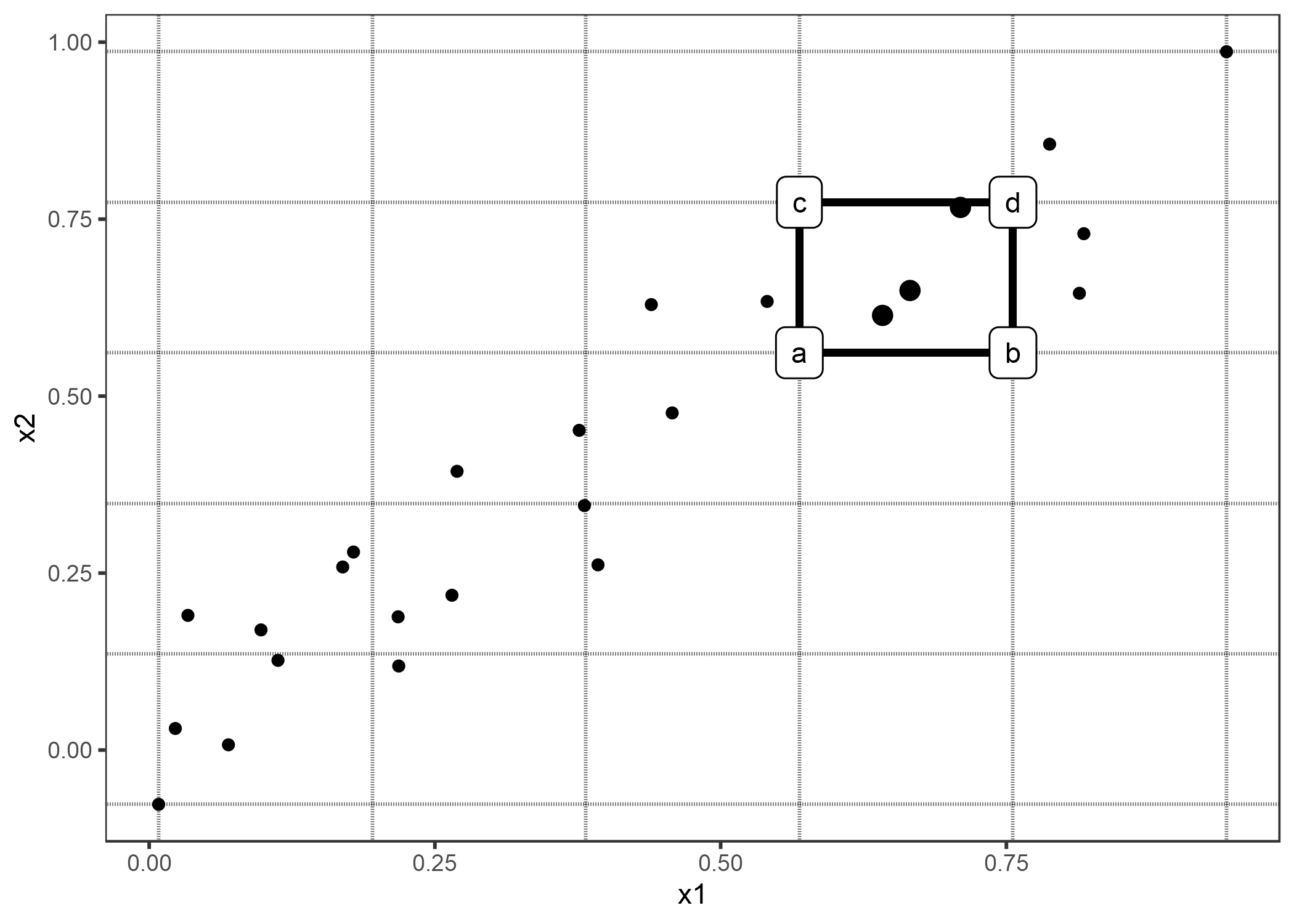
FIGURA 5.13: Cálculo de 2D-ALE. Colocamos una cuadrícula sobre las dos características. En cada celda de la cuadrícula calculamos las diferencias de segundo orden para todas las instancias dentro. Primero reemplazamos los valores de x1 y x2 con los valores de las esquinas de las celdas. Si a, b, c y d representan las predicciones de “esquina” de una instancia manipulada (como se indica en el gráfico), entonces la diferencia de segundo orden es (d - c) - (b - a). La diferencia media de segundo orden en cada celda se acumula sobre la cuadrícula y se centra.

En la figura anterior, muchas celdas están vacías debido a la correlación. En el diagrama ALE, esto se puede visualizar con un cuadro atenuado u oscurecido. Alternativamente, puede reemplazar la estimación de ALE que falta de una celda vacía con la estimación de ALE de la celda no vacía más cercana.

Dado que las estimaciones de ALE para dos características solo muestran el efecto de segundo orden de las características, la interpretación requiere atención especial. El efecto de segundo orden es el efecto de interacción adicional de las características después de haber contabilizado los efectos principales de las características. Supongamos que dos características no interactúan, pero cada una tiene un efecto lineal sobre el resultado predicho. En el gráfico 1D ALE para cada entidad, veríamos una línea recta como la curva ALE estimada. Pero cuando graficamos las estimaciones 2D ALE, deberían estar cerca de cero, porque el efecto de segundo orden es solo el efecto adicional de la interacción. Las gráficas ALE y PD son diferentes en este sentido: Los PDP siempre muestran el efecto total, los gráficos ALE muestran el efecto de primer o segundo orden. Estas son decisiones de diseño que no dependen de las matemáticas subyacentes. Puede restar los efectos de orden inferior en un gráfico de dependencia parcial para obtener los efectos puros principales o de segundo orden o puede obtener una estimación del total de gráficos de ALE evitando restar los efectos de orden inferior.

Los efectos locales acumulados también podrían calcularse para órdenes arbitrariamente más altas (interacciones de tres o más características), pero como se argumenta en el capítulo PDP, solo tiene sentido hasta dos características, porque las interacciones más altas no se pueden visualizar o incluso interpretado de manera significativa.

ALE para características categóricas

El método de efectos locales acumulados necesita, por definición, los valores de las características para tener un orden, porque el método acumula efectos en una determinada dirección. Las características categóricas no tienen ningún orden natural. Para calcular un gráfico ALE para una característica categórica, tenemos que crear o encontrar un pedido de alguna manera. El orden de las categorías influye en el cálculo e interpretación de los efectos locales acumulados.

Una solución es ordenar las categorías según su similitud en función de las otras características. La distancia entre dos categorías es la suma de las distancias de cada entidad. La distancia en función de las características compara la distribución acumulativa en ambas categorías, también llamada distancia de Kolmogorov-Smirnov (para características numéricas) o las tablas de frecuencias relativas (para características categóricas). Una vez que tenemos las distancias entre todas las categorías, usamos escalas multidimensionales para reducir la matriz de distancia a una medida de distancia unidimensional. Esto nos da un orden de similitud basado en las categorías.

Para aclarar esto un poco, aquí hay un ejemplo: Supongamos que tenemos las dos características categóricas “estación” y “clima” y una característica numérica “temperatura”. Para la primera característica categórica (estación) queremos calcular los ALE. La variable tiene las categorías “primavera”, “verano”, “otoño”, “invierno”. Comenzamos a calcular la distancia entre las categorías “primavera” y “verano”. La distancia es la suma de distancias sobre la temperatura y el clima de las características. Para la temperatura, tomamos todas las instancias con la temporada “primavera”, calculamos la función empírica de distribución acumulativa y hacemos lo mismo para las instancias con la temporada “verano” y medimos su distancia con la estadística de Kolmogorov-Smirnov. Para la característica del clima, calculamos para todas las instancias de “primavera” las probabilidades para cada tipo de clima, hacemos lo mismo para las instancias de “verano” y sumamos las distancias absolutas en la distribución de probabilidad. Si “primavera” y “verano” tienen temperaturas y clima muy diferentes, la distancia total por categoría es grande. Repetimos el procedimiento con los otros pares estacionales y reducimos la matriz de distancias resultante a una sola dimensión mediante escalamiento multidimensional.

5.3.4 Ejemplos

Veamos las gráficas ALE en acción. He construido un escenario en el que los PDP fallan. El escenario consiste en un modelo de predicción y dos características fuertemente correlacionadas. El modelo de predicción es principalmente un modelo de regresión lineal, pero hace algo extraño en una combinación de las dos características para las cuales nunca hemos observado casos.

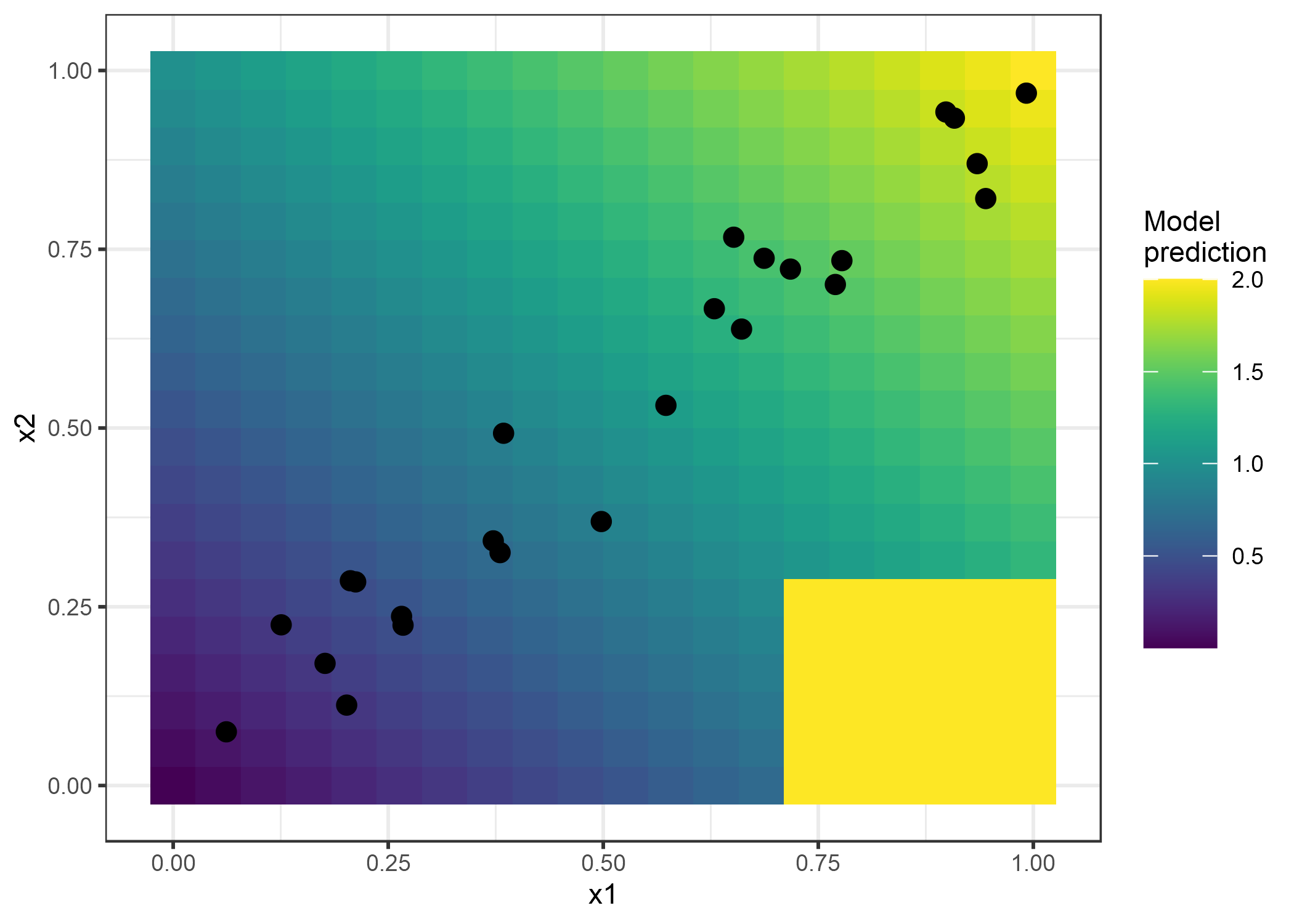
FIGURA 5.14: Dos características y el resultado predicho. El modelo predice la suma de las dos características (fondo sombreado), con la excepción de que si x1 es mayor que 0.7 y x2 menor que 0.3, el modelo siempre predice 2. Esta área está lejos de la distribución de datos (nube de puntos) y no afecta el rendimiento del modelo y tampoco debería afectar su interpretación.

¿Es este un escenario realista y relevante en absoluto? Cuando entrenas un modelo, el algoritmo de aprendizaje minimiza la pérdida de las instancias de datos de entrenamiento existentes. Pueden ocurrir cosas extrañas fuera de la distribución de datos de entrenamiento, porque el modelo no está penalizado por hacer cosas extrañas en estas áreas. Salir de la distribución de datos se llama extrapolación, que también se puede utilizar para engañar a los modelos de aprendizaje automático, que se describe en el capítulo sobre ejemplos adversos. Vea en nuestro pequeño ejemplo cómo se comportan las gráficas de dependencia parcial en comparación con las gráficas ALE.

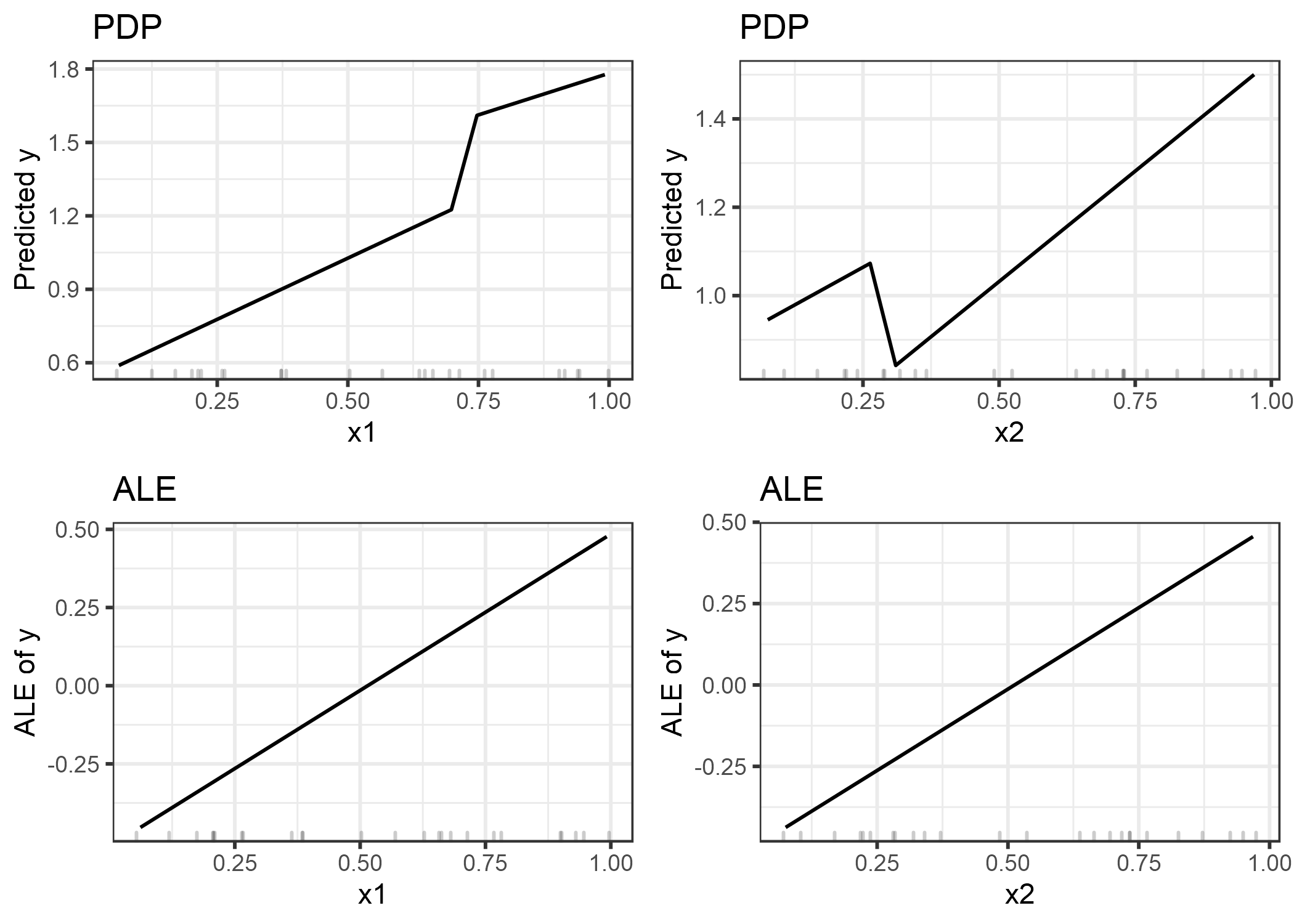
FIGURA 5.15: Comparación de los efectos característicos calculados con PDP (fila superior) y ALE (fila inferior). Las estimaciones de PDP están influenciadas por el comportamiento extraño del modelo externo la distribución de datos (saltos pronunciados en las gráficas). Las gráficas ALE identifican correctamente que el modelo de aprendizaje automático tiene una relación lineal entre las características y la predicción, ignorando las áreas sin datos.

Pero, ¿no es interesante ver que nuestro modelo se comporta de manera extraña en x1>0.7 y x2<0.3? Pues sí y no. Dado que estas son instancias de datos que pueden ser físicamente imposibles o al menos extremadamente improbables, generalmente es irrelevante analizar estas instancias. Pero si sospechas que tu distribución de prueba puede ser ligeramente diferente y algunas instancias están realmente en ese rango, entonces sería interesante incluir esta área en el cálculo de los efectos de características. Pero tiene que ser una decisión consciente incluir áreas donde aún no hemos observado datos y no debe ser un efecto secundario del método de elección como PDP. Si sospechas que el modelo se usará más tarde con datos distribuidos de manera diferente, te recomiendo usar gráficos ALE y simular la distribución de datos que esperas.

En cuanto a un conjunto de datos real, pronostiquemos el número de bicicletas alquiladas según el clima y el día y verifiquemos si las gráficas ALE realmente funcionan tan bien como se prometió. Entrenamos un árbol de regresión para predecir el número de bicicletas alquiladas en un día determinado y utilizamos gráficas ALE para analizar cómo la temperatura, la humedad relativa y la velocidad del viento influyen en las predicciones. Veamos lo que dicen las gráficas ALE:

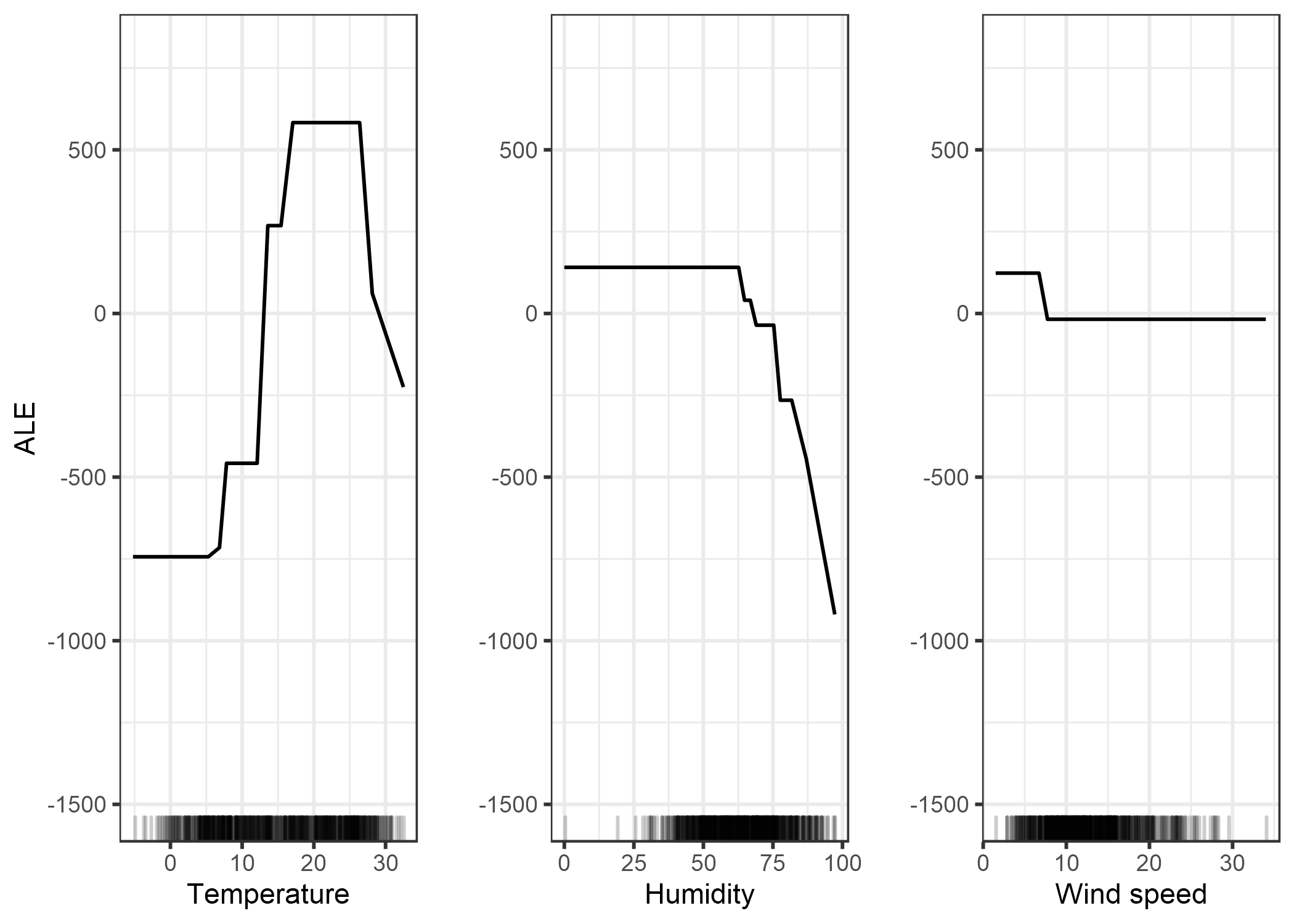
FIGURA 5.16: Gráficos ALE para el modelo de predicción de bicicletas por temperatura, humedad y velocidad del viento. La temperatura tiene un efecto fuerte en la predicción. La predicción promedio crece con el incremento de la temperatura, pero decrece sobre los 25 grados Celsius. La humedad tiene un efecto negativo: sobre el 60%, la más alta humedad baja la predicción. La velocidad del vientono afecta la predicción demasiado.

Veamos la correlación entre temperatura, humedad y velocidad del viento y todas las demás características. Dado que los datos también contienen características categóricas, no solo podemos usar el coeficiente de correlación de Pearson, que solo funciona si ambas características son numéricas. En cambio, entreno un modelo lineal para predecir, por ejemplo, la temperatura basada en una de las otras características como entrada. Luego mido cuánta varianza explica la otra característica en el modelo lineal y tomo la raíz cuadrada. Si la otra característica era numérica, entonces el resultado es igual al valor absoluto del coeficiente de correlación de Pearson estándar. Pero este enfoque basado en modelos de “explicación por la varianza” (también llamado ANOVA, que significa Análisis de varianza) funciona incluso si la otra característica es categórica. La medida “explicada por la varianza” se encuentra siempre entre 0 (sin asociación) y 1 (la temperatura puede predecirse perfectamente a partir de la otra característica). Calculamos la varianza explicada de temperatura, humedad y velocidad del viento con todas las demás características. Cuanto mayor sea la varianza explicada (correlación), más problemas (potenciales) con los gráficos de DP. La siguiente figura visualiza cuán fuertemente se correlacionan las características climáticas con otras características.

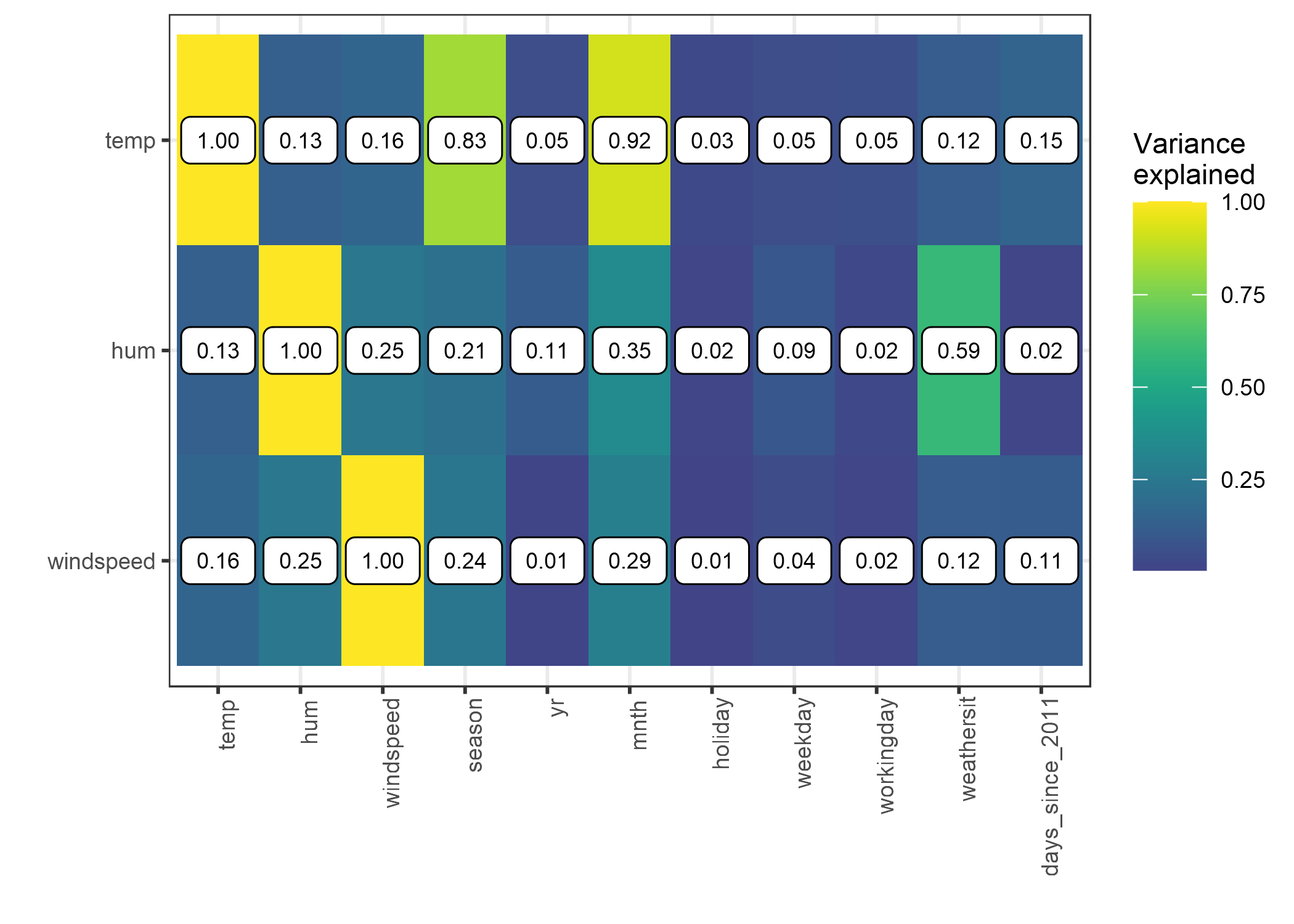
FIGURA 5.17: La fuerza de la correlación entre temperatura, humedad y velocidad del viento con todas las características, medida como la cantidad de variación explicada, cuando entrenamos un modelo lineal con, por ejemplo, temperatura para predecir y estación como característica. Para la temperatura observamos, no sorprendentemente, una alta correlación con la estación y el mes. La humedad se correlaciona con la situación climática.

Este análisis de correlación revela que podemos encontrar problemas con los gráficos de dependencia parcial, especialmente para la característica de temperatura. Bueno, compruébalo tú mismo:

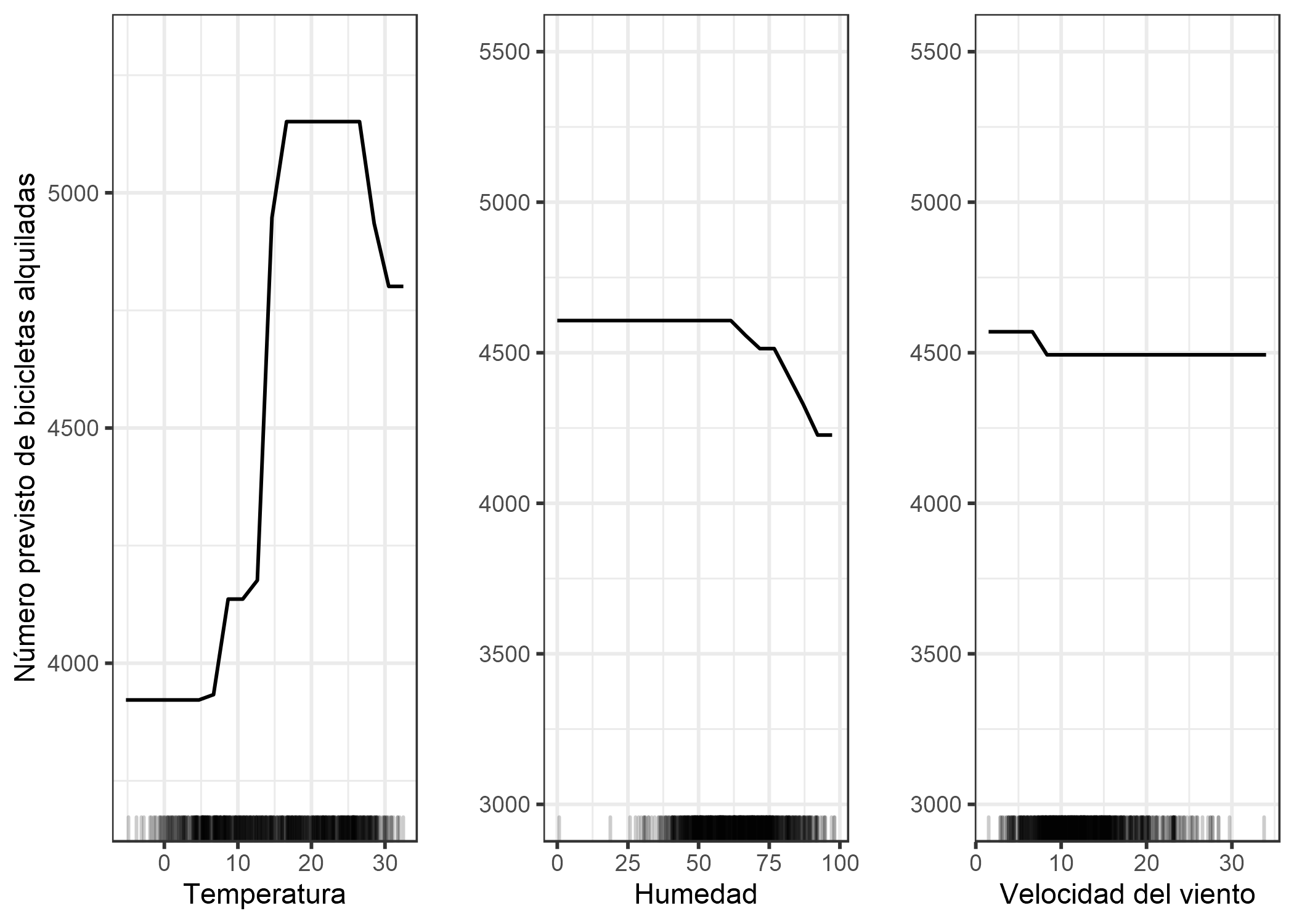
FIGURA 5.18: PDP para temperatura, humedad y velocidad del viento. En comparación con las gráficas ALE, las PDP muestran una disminución menor en el número previsto de bicicletas para alta temperatura o alta humedad. El PDP utiliza todas las instancias de datos para calcular el efecto de las altas temperaturas, incluso si son, por ejemplo, instancias con la temporada “invierno”. Las gráficas ALE son más confiables.

A continuación, veamos los gráficos ALE en acción para una característica categórica. El mes es una característica categórica para la que queremos analizar el efecto sobre el número previsto de bicicletas. Podría decirse que los meses ya tienen un cierto orden (enero a diciembre), pero intentemos ver qué sucede si primero reordenamos las categorías por similitud y luego calculamos los efectos. Los meses se ordenan por la similitud de días de cada mes en función de otras características, como la temperatura o si es feriado.

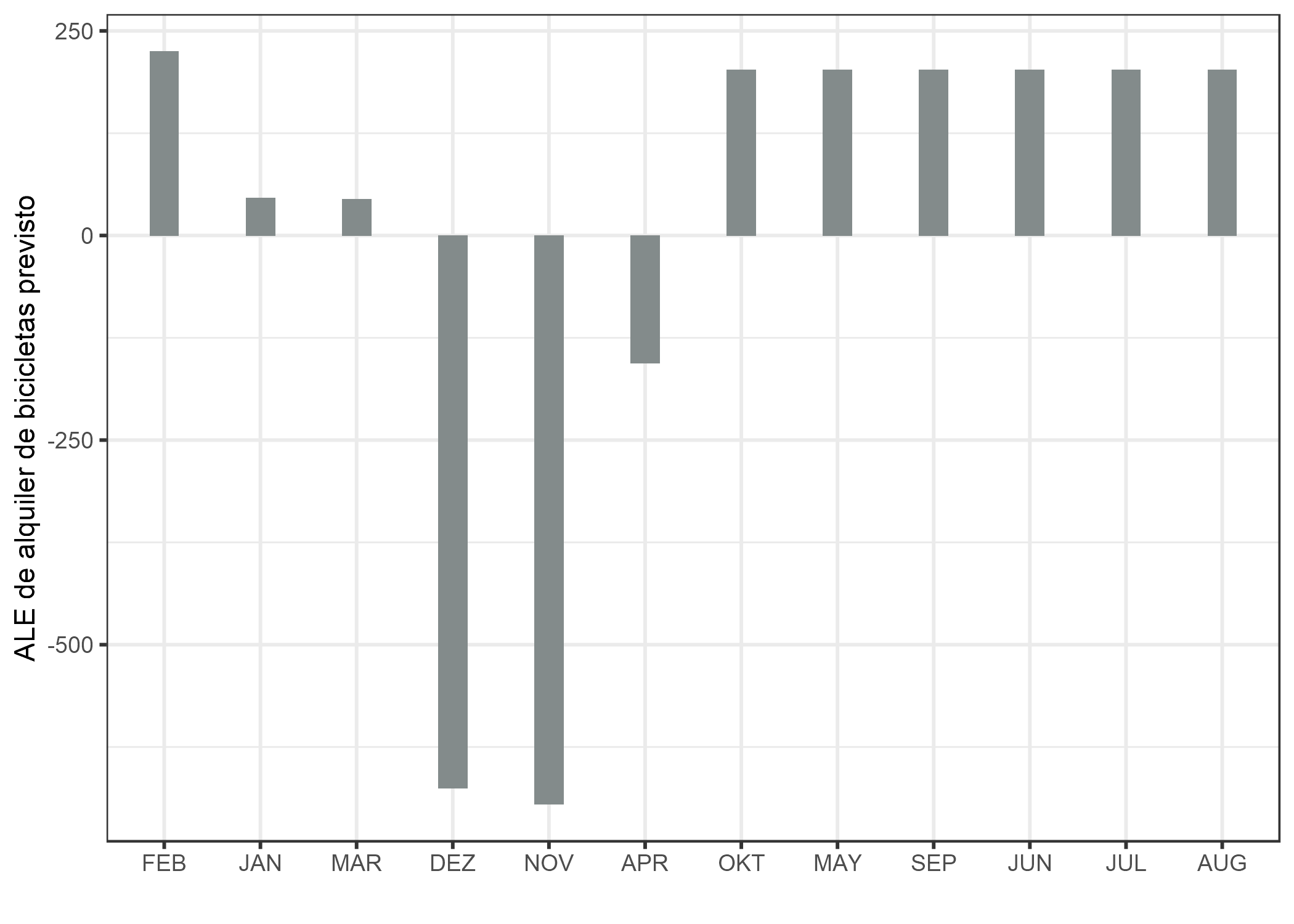
FIGURA 5.19: Gráfico ALE para el mes de la característica categórica. Los meses se ordenan por su similitud entre sí, según las distribuciones de las otras funciones por mes. Observamos que enero, marzo y abril, pero especialmente diciembre y noviembre, tienen un efecto menor en el número previsto de bicicletas alquiladas en comparación con los otros meses.

Dado que muchas de las características están relacionadas con el clima, el orden de los meses refleja fuertemente cuán similar es el clima entre los meses. Todos los meses más fríos están en el lado izquierdo (febrero a abril) y los meses más cálidos en el lado derecho (octubre a agosto). Ten en cuenta que las características no meteorológicas también se han incluido en el cálculo de similitud, por ejemplo, la frecuencia relativa de vacaciones tiene el mismo peso que la temperatura para calcular la similitud entre los meses.

A continuación, consideramos el efecto de segundo orden de la humedad y la temperatura en el número previsto de bicicletas. Recuerda que el efecto de segundo orden es el efecto de interacción adicional de las dos características y no incluye los efectos principales. Esto significa que, por ejemplo, no verás el efecto principal de que la alta humedad conduce a un menor número de bicicletas predichas en promedio en el diagrama ALE de segundo orden.

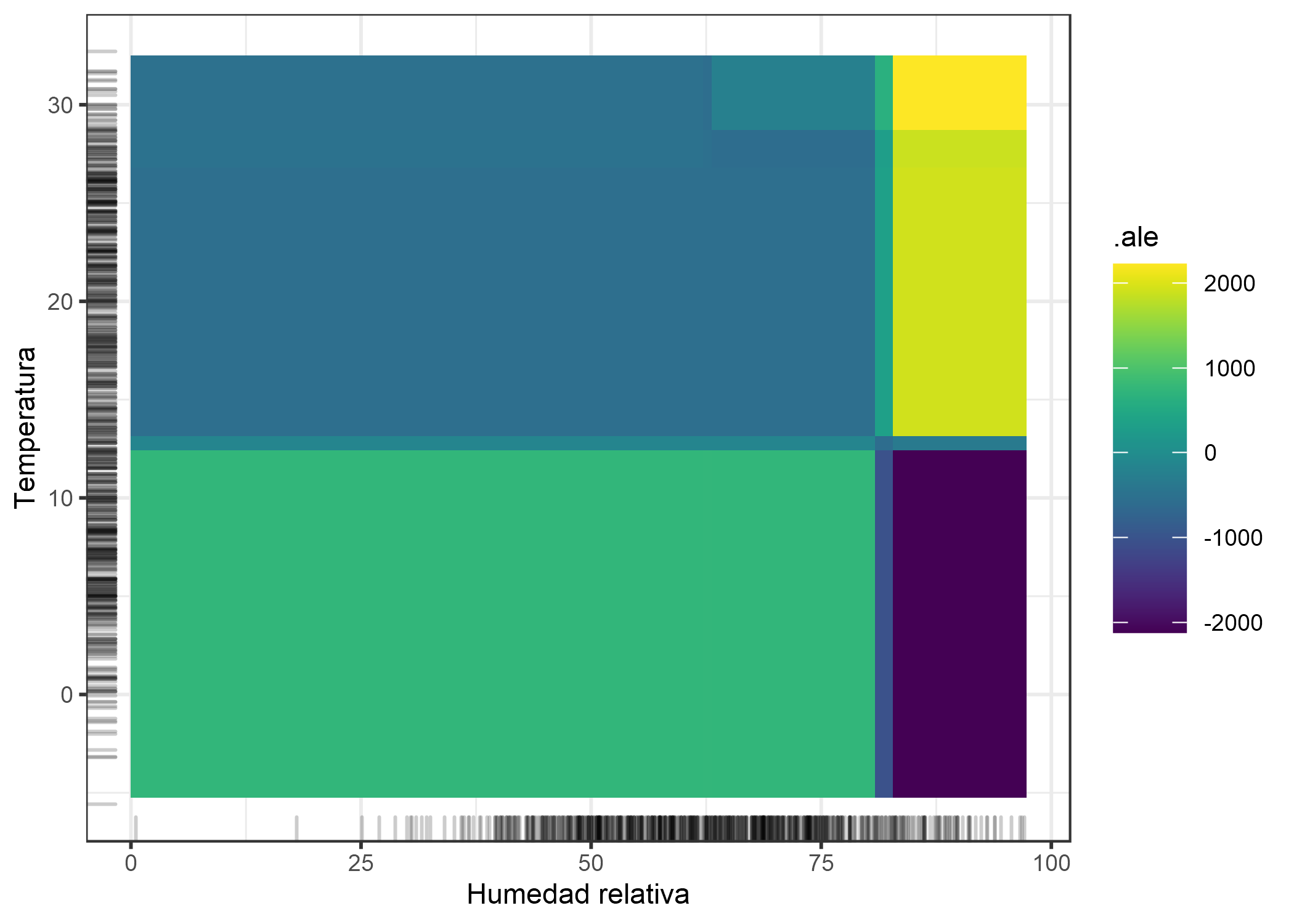
FIGURA 5.20: Gráfico ALE para el efecto de segundo orden de la humedad y la temperatura en el número previsto de bicicletas alquiladas. El tono más claro indica un tono por encima del promedio y el más oscuro una predicción por debajo del promedio cuando los efectos principales ya se tienen en cuenta. La trama revela una interacción entre temperatura y humedad: el clima cálido y húmedo aumenta la predicción. En climas fríos y húmedos se muestra un efecto negativo adicional en el número de bicicletas predichas.

Ten en cuenta que los dos efectos principales de la humedad y la temperatura indican que el número previsto de bicicletas disminuye en climas muy cálidos y húmedos. En climas cálidos y húmedos, el efecto combinado de temperatura y humedad no es, por lo tanto, la suma de los efectos principales, sino mayor que la suma. Para enfatizar la diferencia entre el efecto de segundo orden puro (el gráfico 2D ALE que acaba de ver) y el efecto total, veamos el gráfico de dependencia parcial. El PDP muestra el efecto total, que combina la predicción media, los dos efectos principales y el efecto de segundo orden (la interacción).

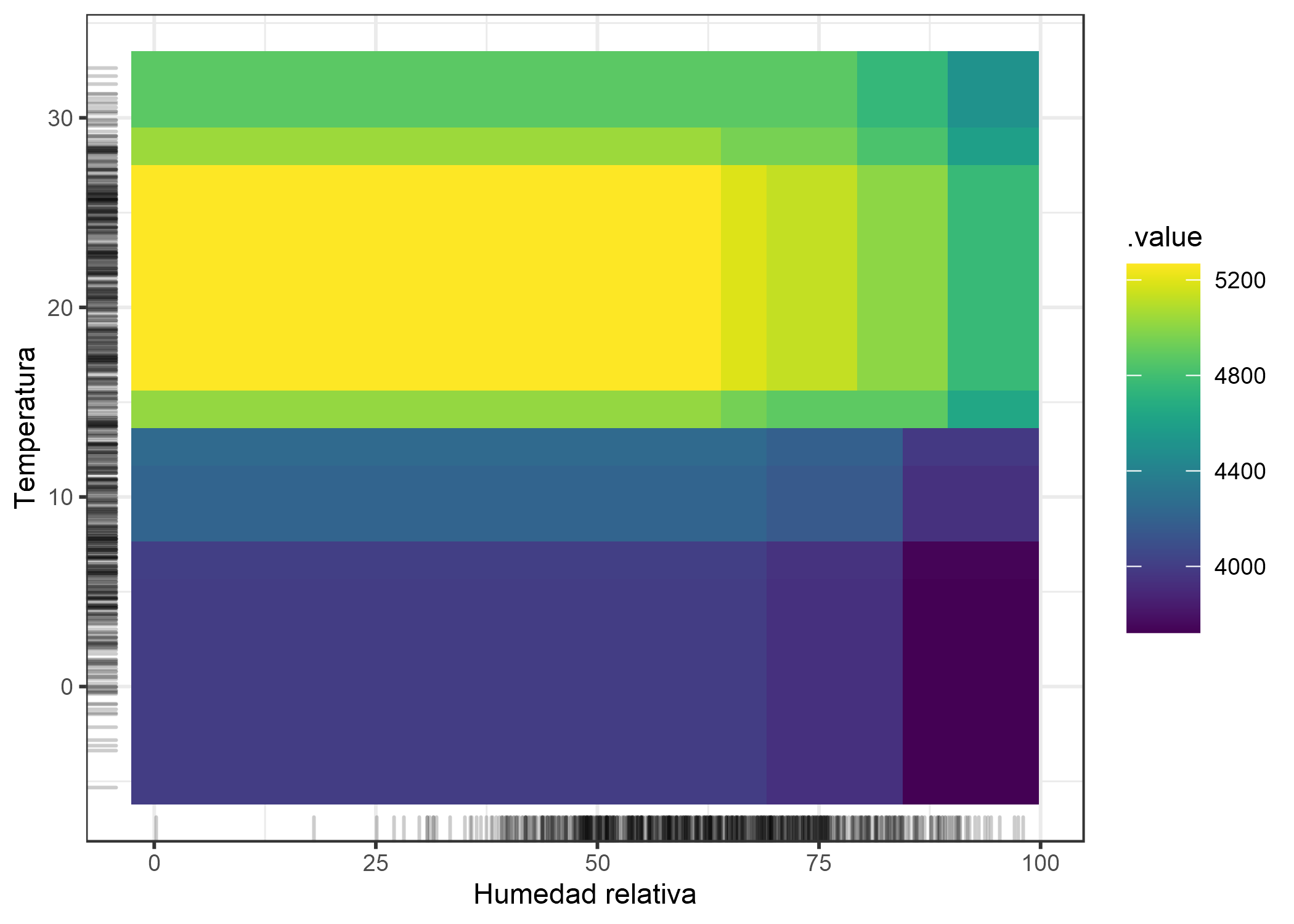
FIGURA 5.21: PDP del efecto total de la temperatura y la humedad en el número previsto de bicicletas. La trama combina el efecto principal de cada una de las características y su interacción efecto, a diferencia del gráfico 2D-ALE que solo muestra la interacción.

Si solo estás interesado en la interacción, debes mirar los efectos de segundo orden, ya que el efecto total mezcla los efectos principales en la trama. Pero si deseas conocer el efecto combinado de las características, debes mirar el efecto total (que muestra el PDP). Por ejemplo, si deseas conocer el número esperado de bicicletas a 30 grados Celsius y 80 por ciento de humedad, puedes leerlo directamente desde el PDP 2D. Si deseas leer lo mismo de los gráficos ALE, debes mirar tres gráficos: El gráfico ALE para temperatura, humedad y temperatura + humedad y también necesitas conocer la predicción media general. En un escenario donde dos características no tienen interacción, la gráfica de efecto total de las dos características podría ser engañosa porque probablemente muestra un paisaje complejo, lo que sugiere cierta interacción, pero es simplemente el producto de los dos efectos principales. El efecto de segundo orden mostraría inmediatamente que no hay interacción.

Suficientes bicicletas por ahora, pasemos a una tarea de clasificación. Entrenamos un random forest para predecir la probabilidad de cáncer cervical en función de los factores de riesgo. Visualizamos los efectos locales acumulados para dos de las características:

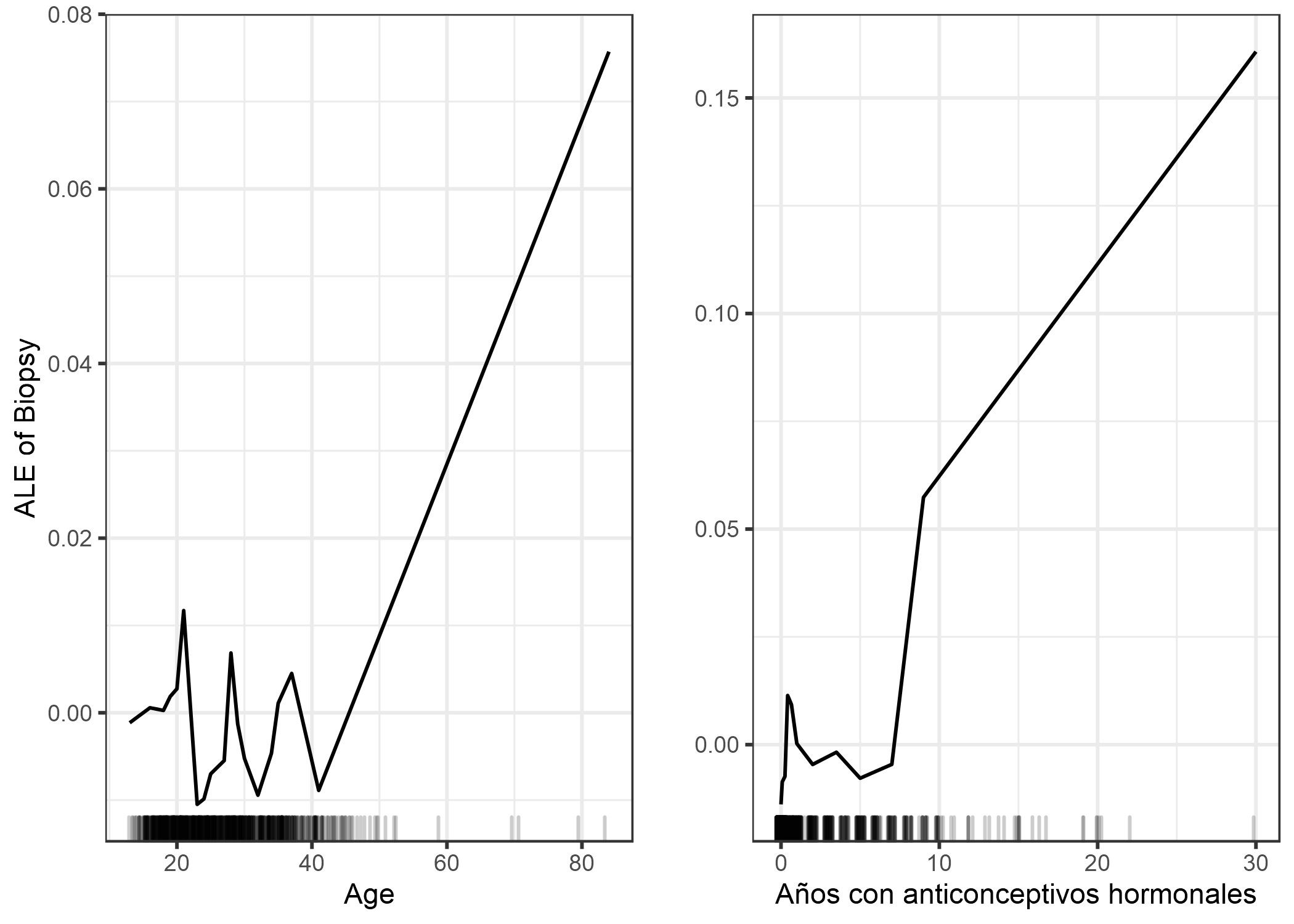
FIGURA 5.22: Gráfica ALE del efecto de la edad y los años con anticonceptivos hormonales en la probabilidad pronosticada de cáncer cervical. Para la característica de edad, la gráfica ALE muestra que la probabilidad pronosticada de cáncer es bajo en promedio hasta los 40 años y aumenta después de eso. El número de años con anticonceptivos hormonales se asocia con un mayor riesgo de cáncer previsto después de 8 años.

A continuación, observamos la interacción entre el número de embarazos y la edad.

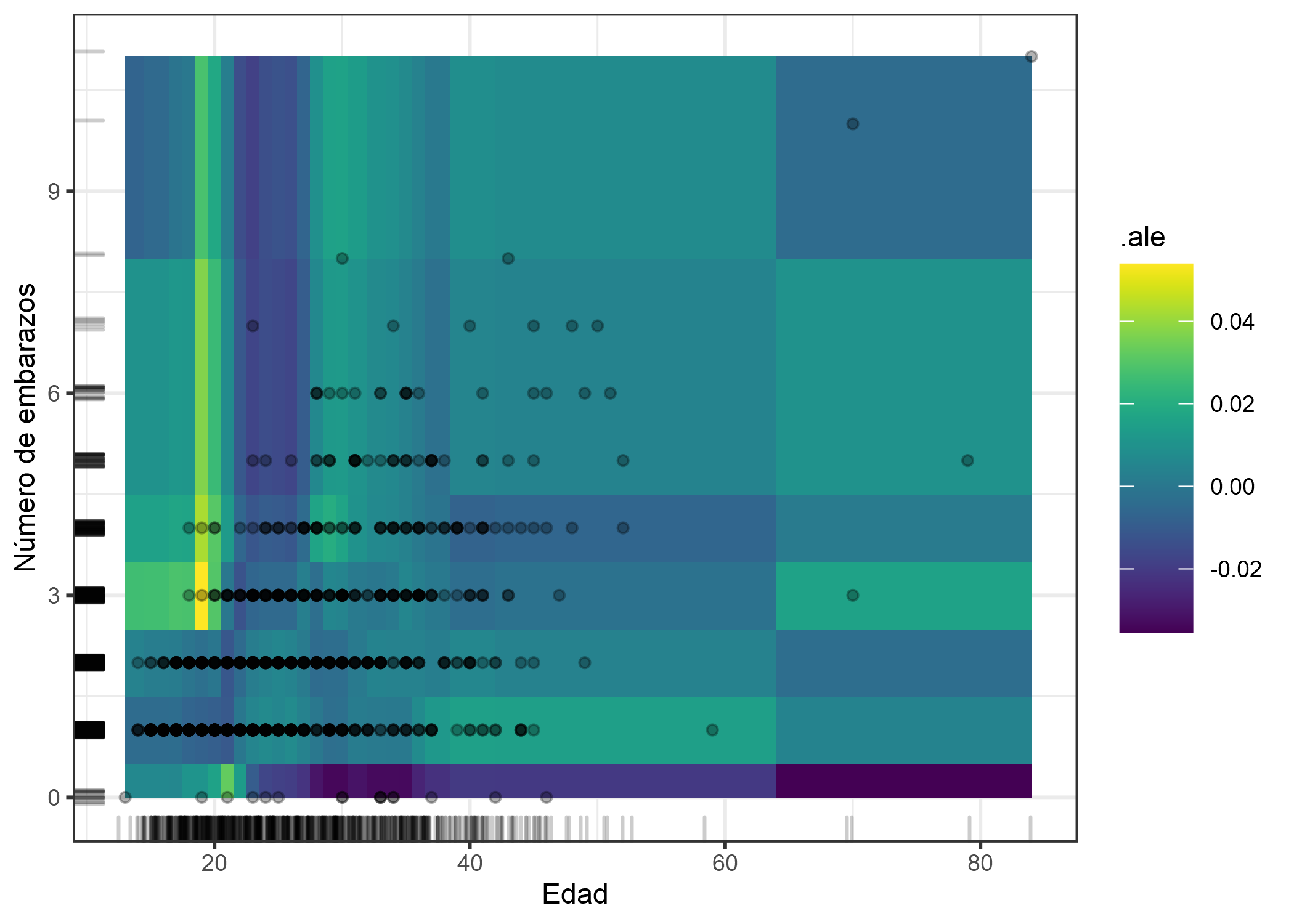
FIGURA 5.23: Gráfico ALE del efecto de segundo orden del número de embarazos y la edad. La interpretación de la trama no es concluyente, ya que muestra lo que parece un sobreajuste. Por ejemplo, la gráfica muestra un comportamiento de modelo extraño a la edad de 18-20 años y más de 3 embarazos (aumento de hasta 5 puntos porcentuales en la probabilidad de cáncer). No hay muchas mujeres en los datos con esta constelación de edad y número de embarazos (los datos reales se muestran como puntos), por lo que el modelo no se penaliza severamente durante el entrenamiento por cometer errores para esas mujeres.

5.3.5 Ventajas

Las gráficas ALE son imparciales, lo que significa que aún funcionan cuando las características están correlacionadas. Las gráficas de dependencia parcial fallan en este escenario porque marginaron sobre combinaciones de valores de características improbables o incluso físicamente imposibles.

Los gráficos ALE son más rápidos de calcular que los PDP y se escalan con O(n), ya que el mayor número posible de intervalos es el número de instancias con un intervalo por instancia. El PDP requiere n veces el número de estimaciones de puntos de la cuadrícula. Para 20 puntos de cuadrícula, los PDP requieren 20 veces más predicciones que el gráfico ALE del caso más desfavorable donde se utilizan tantos intervalos como instancias.

La interpretación de las gráficas ALE es clara: dependiendo de un valor dado, el efecto relativo de cambiar la característica en la predicción se puede leer de la gráfica ALE. Las gráficas ALE están centradas en cero. Esto hace que su interpretación sea agradable, porque el valor en cada punto de la curva ALE es la diferencia con la predicción media. El diagrama 2D ALE solo muestra la interacción: Si dos características no interactúan, la trama no muestra nada.

En general, en la mayoría de las situaciones preferiría las gráficas ALE a las PDP, porque las características generalmente están correlacionadas en cierta medida.

5.3.6 Desventajas

Las gráficas ALE pueden volverse un poco inestables (muchas subidas y bajadas pequeñas) con una gran cantidad de intervalos. En este caso, reducir el número de intervalos hace que las estimaciones sean más estables, pero también suaviza y oculta parte de la verdadera complejidad del modelo de predicción. No existe una solución perfecta para establecer el número de intervalos. Si el número es demasiado pequeño, los gráficos ALE pueden no ser muy precisos. Si el número es demasiado alto, la curva puede volverse inestable.

A diferencia de los PDP, los gráficos ALE no están acompañados por curvas ICE. Para los PDP, las curvas ICE son excelentes porque pueden revelar heterogeneidad en el efecto de la característica, lo que significa que el efecto de una característica se ve diferente para los subconjuntos de datos. Para los gráficos ALE solo puede verificar por intervalo si el efecto es diferente entre las instancias, pero cada intervalo tiene instancias diferentes, por lo que no es lo mismo que las curvas ICE.

Las estimaciones de ALE de segundo orden tienen una estabilidad variable en todo el espacio de características, que no se visualiza de ninguna manera. La razón de esto es que cada estimación de un efecto local en una celda utiliza un número diferente de instancias de datos. Como resultado, todas las estimaciones tienen una precisión diferente (pero siguen siendo las mejores estimaciones posibles). El problema existe en una versión menos severa para los gráficos ALE de efecto principal. El número de instancias es el mismo en todos los intervalos, gracias al uso de cuantiles como cuadrícula, pero en algunas áreas habrá muchos intervalos cortos y la curva ALE consistirá en muchas más estimaciones. Pero para intervalos largos, que pueden constituir una gran parte de toda la curva, hay comparativamente menos casos. Esto sucedió en la predicción ALE de cáncer de cuello uterino para la edad avanzada, por ejemplo.

Las gráficas de efectos de segundo orden pueden ser un poco molestas de interpretar, ya que siempre debes tener en cuenta los efectos principales. Es tentador leer los mapas de calor como el efecto total de las dos características, pero es solo el efecto adicional de la interacción. El efecto puro de segundo orden es interesante para descubrir y explorar interacciones, pero para interpretar cómo se ve el efecto, creo que tiene más sentido integrar los efectos principales en la trama.

La implementación de los gráficos ALE es mucho más compleja y menos intuitiva en comparación con los gráficos de dependencia parcial.

Aunque los gráficos ALE no están sesgados en caso de características correlacionadas, la interpretación sigue siendo difícil cuando las características están fuertemente correlacionadas. Porque si tienen una correlación muy fuerte, solo tiene sentido analizar el efecto de cambiar ambas características juntas y no de forma aislada. Esta desventaja no es específica de las gráficas ALE, sino un problema general de características fuertemente correlacionadas.

Si las características no están correlacionadas y el tiempo de cálculo no es un problema, los PDP son ligeramente preferibles porque son más fáciles de entender y se pueden trazar junto con las curvas ICE.

La lista de desventajas se ha vuelto bastante larga, pero no te dejes engañar por la cantidad de palabras que uso: Como regla general: usa ALE en lugar de PDP.

5.3.7 Implementación y alternativas

¿Mencioné que los gráficos de dependencia parcial y las curvas de expectativas condicionales individuales son una alternativa? =)

Que yo sepa, las gráficas ALE actualmente solo se implementan en R, en el paquete ALEPlot R creado por el inventor mismo, y en el paquete iml.

---

30. Apley, Daniel W. “Visualizing the effects of predictor variables in black box supervised learning models.” arXiv preprint arXiv:1612.08468 (2016).↩