4.2 Regresión logística
La regresión logística modela las probabilidades en problemas de clasificación con dos resultados posibles. Es una extensión del modelo de regresión lineal para problemas de clasificación.
4.2.1 ¿Qué tiene de malo la regresión lineal para la clasificación?
El modelo de regresión lineal puede funcionar bien para la regresión, pero falla en la clasificación. ¿Por qué? En el caso de dos clases, puedes etiquetar una de las clases con 0 y la otra con 1 y usar regresión lineal. Técnicamente funciona y la mayoría de los programas de modelos lineales devolverán pesos. Pero hay algunos problemas con este enfoque:
Un modelo lineal no genera probabilidades, si no que trata las clases como números (0 y 1) y se ajusta al mejor hiperplano (para una sola característica, es una línea) que minimiza las distancias entre los puntos y el hiperplano. Por lo tanto, simplemente se interpola entre los puntos y no se puede interpretar como probabilidades.
Un modelo lineal también extrapola, por lo que puede dar valores por debajo de cero y por encima de uno. Esta es una señal de que podría haber un enfoque más inteligente para la clasificación.
Dado que el resultado previsto no es una probabilidad, sino una interpolación lineal entre puntos, no existe un umbral significativo en el que pueda distinguir una clase de la otra. Se ha dado una buena ilustración de este problema en Stackoverflow.
Los modelos lineales no se extienden a problemas de clasificación con múltiples clases. Tendrías que comenzar a etiquetar la siguiente clase con 2, luego 3, y así sucesivamente. Aunque es posible que las clases no tengan un orden significativo, el modelo lineal forzaría una estructura extraña en la relación entre las características y las predicciones de su clase. De esta forma, cuanto mayor sea el valor de una característica con un peso positivo, más contribuiria a la predicción de una clase con un número más alto, incluso si las clases que obtienen un número similar no están más cerca que otras clases.
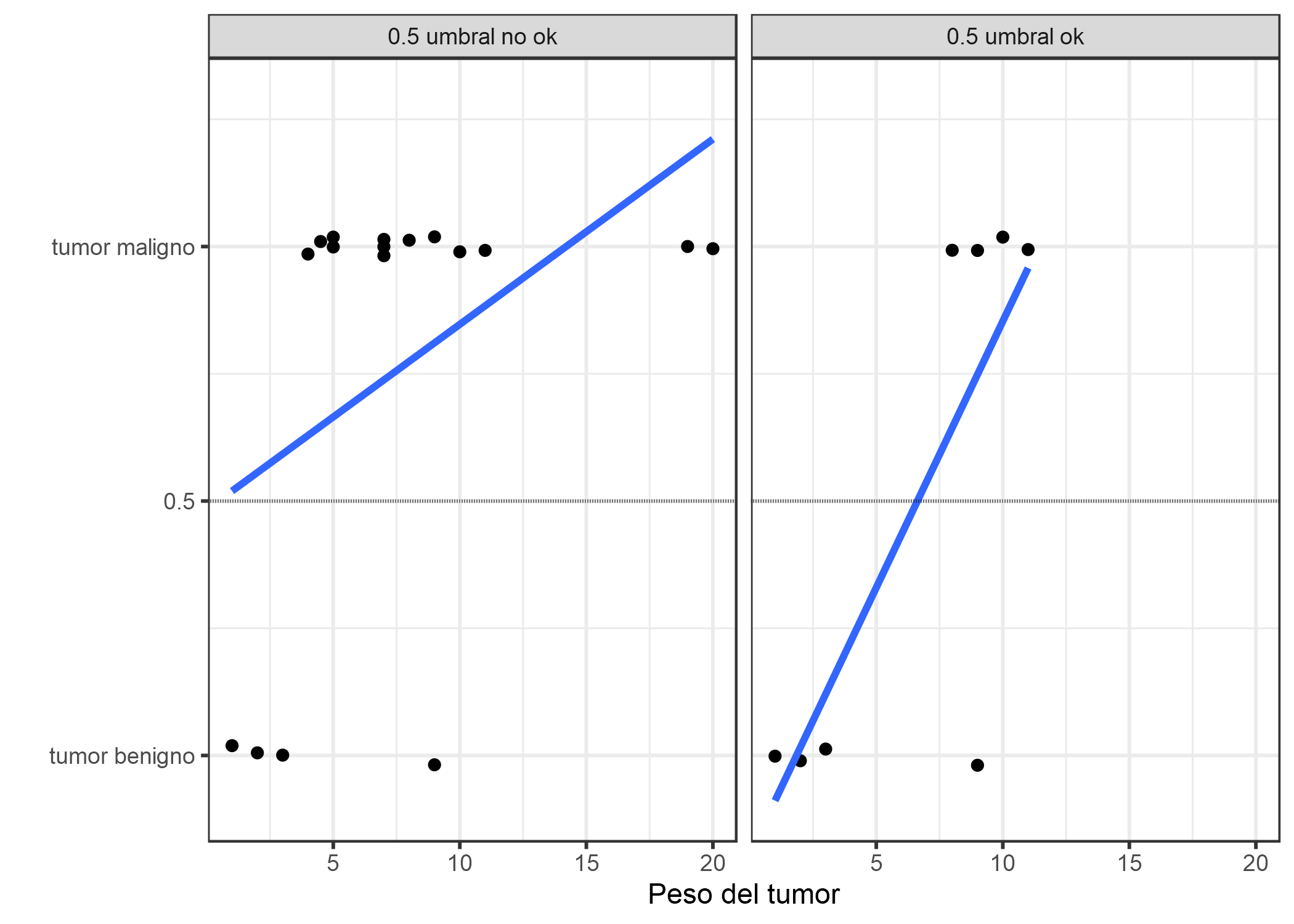
FIGURA 4.5: Un modelo lineal clasifica los tumores como malignos (1) o benignos (0) dado su tamaño. Las líneas muestran la predicción del modelo lineal. Para los datos de la izquierda, podemos usar 0.5 como umbral de clasificación. Después de introducir algunos casos más de tumores malignos, un umbral de 0.5 ya no separa las clases. Los puntos se alteran ligeramente para reducir la sobreimpresión.
4.2.2 Teoría
Una solución para la clasificación es la regresión logística. En lugar de ajustar una línea recta o un hiperplano, el modelo de regresión logística utiliza la función logística para forzar a que la salida de una ecuación lineal esté entre 0 y 1. La función logística se define como:
\[\text{logistic}(\eta)=\frac{1}{1+exp(-\eta)}\]
Y se ve así:
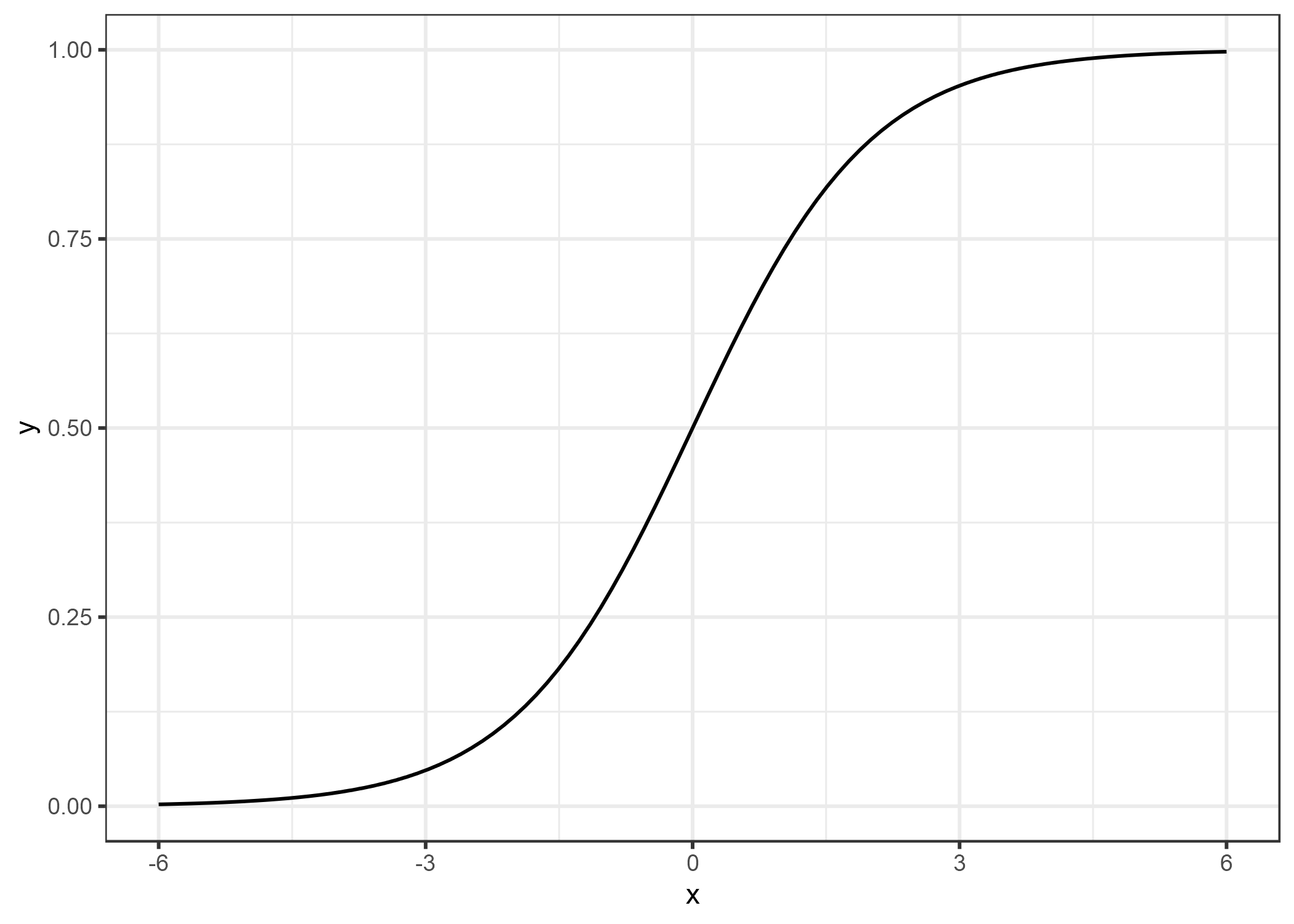
FIGURA 4.6: La función logística. Produce números entre 0 y 1. En la entrada 0, genera 0.5.
El paso de la regresión lineal a la regresión logística es algo sencillo. En el modelo de regresión lineal, hemos modelado la relación entre el resultado y las características con una ecuación lineal:
\[\hat{y}^{(i)}=\beta_{0}+\beta_{1}x^{(i)}_{1}+\ldots+\beta_{p}x^{(i)}_{p}\]
Para la clasificación, preferimos probabilidades entre 0 y 1, por lo que ajustamos el lado derecho de la ecuación a la función logística. Esto obliga a la salida a asumir solo valores entre 0 y 1.
\[P(y^{(i)}=1)=\frac{1}{1+exp(-(\beta_{0}+\beta_{1}x^{(i)}_{1}+\ldots+\beta_{p}x^{(i)}_{p}))}\]
Volvamos al ejemplo del tamaño del tumor nuevamente. Pero en lugar del modelo de regresión lineal, usamos el modelo de regresión logística:
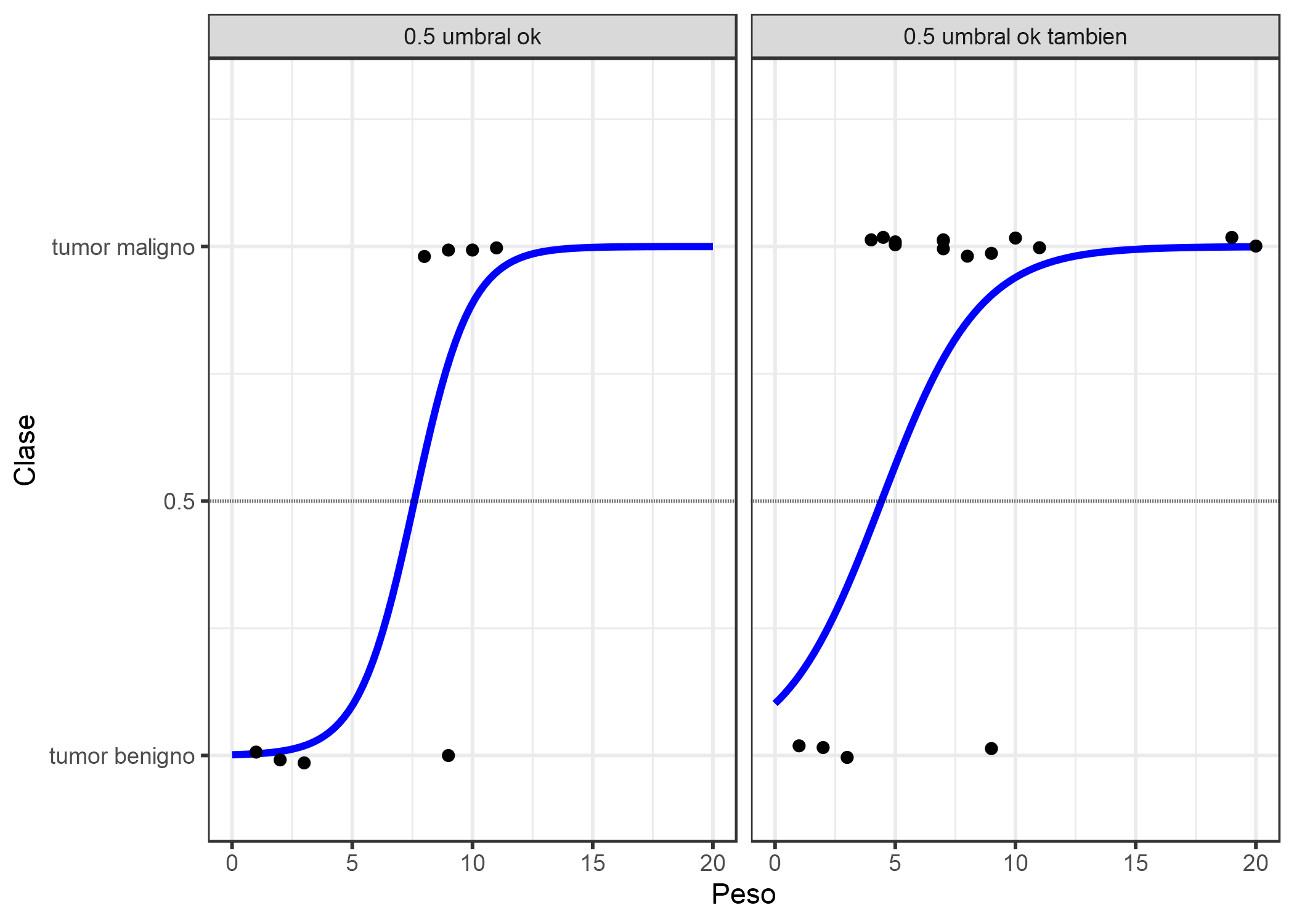
FIGURA 4.7: El modelo de regresión logística encuentra el límite de decisión correcto entre maligno y benigno dependiendo del tamaño del tumor. La línea es la función logística desplazada y exprimida para ajustarse a los datos.
La clasificación funciona mejor con la regresión logística y podemos usar 0.5 como umbral en ambos casos. La inclusión de puntos adicionales no afecta sustancialmente la curva estimada.
4.2.3 Interpretación
La interpretación de los pesos en la regresión logística difiere de la interpretación de los pesos en la regresión lineal, ya que el resultado en la regresión logística es una probabilidad entre 0 y 1. Los pesos ya no influyen en la probabilidad linealmente. La suma ponderada se transforma mediante la función logística en una probabilidad. Por lo tanto, necesitamos reformular la ecuación para la interpretación, de modo que solo el término lineal esté en el lado derecho de la fórmula.
\[log\left(\frac{P(y=1)}{1-P(y=1)}\right)=log\left(\frac{P(y=1)}{P(y=0)}\right)=\beta_{0}+\beta_{1}x_{1}+\ldots+\beta_{p}x_{p}\]
Llamamos al término en la función log() “odds” (chances, probabilidad del evento dividido por probabilidad del no evento), y envuelto en el logaritmo se llama log-odds.
Esta fórmula muestra que el modelo de regresión logística es un modelo lineal para las log-odds. ¡Excelente! ¡Eso no suena útil! Con una pequeña combinación de los términos, puedes descubrir cómo cambia la predicción cuando una de las características \(x_j\) cambia en una unidad. Para hacer esto, primero podemos aplicar la función exp() a ambos lados de la ecuación:
\[\frac{P(y=1)}{1-P(y=1)}=odds=exp\left(\beta_{0}+\beta_{1}x_{1}+\ldots+\beta_{p}x_{p}\right)\]
Luego comparamos lo que sucede cuando aumentamos uno de los valores de la característica en 1. Pero en lugar de mirar la diferencia, miramos el ratio entre las dos predicciones:
\[\frac{odds_{x_j+1}}{odds}=\frac{exp\left(\beta_{0}+\beta_{1}x_{1}+\ldots+\beta_{j}(x_{j}+1)+\ldots+\beta_{p}x_{p}\right)}{exp\left(\beta_{0}+\beta_{1}x_{1}+\ldots+\beta_{j}x_{j}+\ldots+\beta_{p}x_{p}\right)}\]
Aplicamos la siguiente regla:
\[\frac{exp(a)}{exp(b)}=exp(a-b)\]
Y eliminamos muchos términos:
\[\frac{odds_{x_j+1}}{odds}=exp\left(\beta_{j}(x_{j}+1)-\beta_{j}x_{j}\right)=exp\left(\beta_j\right)\]
Al final, tenemos algo tan simple como la exponencial del peso de una característica. Un cambio de una característica en una unidad cambia la razón entre las posibilidades (multiplicativa) por un factor de \(\exp(\beta_j)\). También podríamos interpretarlo de esta manera: Un cambio de \(x_j\) en una unidad aumenta la relación de log-odds en el valor del peso correspondiente. La mayoría de las personas interpretan el ratio de odds, porque se sabe que pensar en el logaritmo de algo es duro para el cerebro. Interpretar el ratio de odds ya requiere acostumbrarse. Por ejemplo, si tienes odds de 2, significa que la probabilidad de y=1 es el doble de y=0. Si tenés un peso (= ratio log-odds) de 0.7, al aumentar la característica respectiva en una unidad multiplica las probabilidades por exp (0.7) (aproximadamente 2) y las odds cambian a 4. Pero, por lo general, no manejas las probabilidades e interpretas los pesos solo como las razones de probabilidades. Porque para calcular realmente las probabilidades, necesitarías establecer un valor para cada característica, lo que solo tiene sentido si deseas ver una instancia específica de su conjunto de datos.
Estas son las interpretaciones para el modelo de regresión logística con diferentes tipos de características:
- Característica numérica: Si aumenta el valor de la variable \(x_{j}\) en una unidad, las probabilidades estimadas cambian en un factor de \(\exp(\beta_{j})\)
- Característica categórica binaria: Uno de los dos valores de la variable es la categoría de referencia o basal (en algunos idiomas, el codificado en 0). Cambiar la variable \(x_{j}\) de la categoría de referencia a la otra categoría cambia las probabilidades estimadas por un factor de \(\exp(\beta_{j})\).
- Característica categórica con más de dos categorías: Una solución para lidiar con múltiples categorías es una hot encoding, lo que significa que cada categoría tiene su propia columna. Solo necesita L-1 columnas para una característica categórica con L categorías, de lo contrario está sobre-parametrizada. La categoría L-ésima es entonces la categoría de referencia. Puedes usar cualquier otra codificación que puedas usar en regresión lineal. La interpretación para cada categoría es equivalente a la interpretación de características binarias.
- Intercepto \(\beta_{0}\): Cuando todas las características numéricas son cero y las características categóricas están en la categoría de referencia, las probabilidades estimadas son \(\exp(\beta_{0})\). La interpretación del peso del intercepto generalmente no es relevante.
4.2.4 Ejemplo
Utilizamos el modelo de regresión logística para predecir cáncer cervical en función de algunos factores de riesgo. La siguiente tabla muestra los pesos estimados, las razones de odds asociadas y el error estándar de las estimaciones.
| Weight | Odds ratio | Std. Error | |
|---|---|---|---|
| Intercept | 2.91 | 18.36 | 0.32 |
| Hormonal contraceptives y/n | 0.12 | 1.12 | 0.30 |
| Smokes y/n | -0.26 | 0.77 | 0.37 |
| Num. of pregnancies | -0.04 | 0.96 | 0.10 |
| Num. of diagnosed STDs | -0.82 | 0.44 | 0.33 |
| Intrauterine device y/n | -0.62 | 0.54 | 0.40 |
Interpretación de una característica numérica (“Num. of diagnosed STDs”): Un aumento en el número de ETS (enfermedades de transmisión sexual) diagnosticadas cambia (aumenta) las probabilidades de cáncer frente a ausencia de cáncer por un factor de 0.44, cuando todas las demás características siguen siendo las mismas. Ten en cuenta que la correlación no implica causalidad.
Interpretación de una característica categórica (“Anticonceptivos hormonales si/no”): Para las mujeres que usan anticonceptivos hormonales, las probabilidades de cáncer versus no cáncer son por un factor 1.12 menor, en comparación con las mujeres sin anticonceptivos hormonales, dado que todas las demás características permanecen igual.
Al igual que en el modelo lineal, las interpretaciones siempre vienen con la cláusula de que “todas las demás características permanecen igual”.
4.2.5 Ventajas y desventajas
Muchos de los pros y los contras del modelo de regresión lineal también se aplican al modelo de regresión logística. La regresión logística ha sido ampliamente utilizada por muchas personas diferentes, pero lucha con su expresividad restrictiva (por ejemplo, las interacciones deben agregarse manualmente). Otros modelos pueden tener un mejor rendimiento predictivo.
Otra desventaja del modelo de regresión logística es que la interpretación es más difícil porque la interpretación de los pesos es multiplicativa y no aditiva.
La regresión logística puede sufrir de separación completa. Si hay una característica que separe perfectamente las dos clases, el modelo de regresión logística ya no puede ser entrenado. Esto se debe a que el peso de esa característica no convergería, porque el peso óptimo sería infinito. Esto parece ser un poco desafortunado, porque tal característica es realmente útil. Sin embargo, no necesitas aprendizaje automático si tienes una regla simple que separa ambas clases. El problema de la separación completa se puede resolver introduciendo la penalización de los pesos o definiendo una distribución de probabilidad previa de los pesos.
En el lado bueno, el modelo de regresión logística no es solo un modelo de clasificación, sino que también brinda probabilidades. Esta es una gran ventaja sobre los modelos que solo pueden proporcionar la clasificación final. Saber que una observación tiene una probabilidad del 99% para una clase en comparación con el 51% hace una gran diferencia.
La regresión logística también puede extenderse de la clasificación binaria a la clasificación multiclase. Entonces se llama Regresión Multinomial.
4.2.6 Software
Usé la función glm en R para todos los ejemplos.
Puedes encontrar regresión logística en cualquier lenguaje de programación que pueda usarse para realizar análisis de datos, como Python, Java, Stata, Matlab, …