5.4 Interacción de características
Cuando las características interactúan entre sí en un modelo de predicción, la predicción no puede expresarse como la suma de los efectos de cada característica, porque el efecto de una característica depende del valor de la otra característica. El predicado de Aristóteles “El todo es mayor que la suma de sus partes” se aplica en presencia de interacciones.
5.4.1 Interacción de características
Si un modelo de aprendizaje automático realiza una predicción basada en dos características, podemos descomponer la predicción en cuatro términos: un término constante, un término para la primera característica, un término para la segunda característica y un término para la interacción entre las dos características. La interacción entre dos características es el cambio en la predicción que ocurre al variar las características después de considerar los efectos de las características individuales.
Por ejemplo, un modelo predice el valor de una casa, utilizando el tamaño de la casa (grande o pequeña) y la ubicación (buena o mala) como características, lo que arroja cuatro posibles predicciones:
| Ubicación | Tamaño | Predicción |
|---|---|---|
| buena | grande | 300,000 |
| buena | pequeña | 200,000 |
| mala | grande | 250,000 |
| mala | pequeña | 150,000 |
Descomponemos la predicción del modelo en las siguientes partes: Un término constante (150,000), un efecto para la característica de tamaño (+100,000 si es grande; +0 si es pequeña) y un efecto para la ubicación (+50,000 si es bueno; +0 si es malo). Esta descomposición explica completamente las predicciones del modelo. No hay efecto de interacción, porque la predicción del modelo es una suma de los efectos de características individuales para el tamaño y la ubicación. Cuando se hace grande una casa pequeña, la predicción siempre aumenta en 100,000, independientemente de la ubicación. Además, la diferencia en la predicción entre una buena y una mala ubicación es de 50,000, independientemente del tamaño.
Veamos ahora un ejemplo con interacción:
| Ubicación | Tamaño | Predicción |
|---|---|---|
| buena | grande | 400,000 |
| buena | pequeña | 200,000 |
| mala | grande | 250,000 |
| mala | pequeña | 150,000 |
Descomponemos la tabla de predicción en las siguientes partes: Un término constante (150,000), un efecto para la característica de tamaño (+100,000 si es grande, +0 si es pequeña) y un efecto para la ubicación (+50,000 si es bueno, +0 si es malo). Para esta tabla, necesitamos un término adicional para la interacción: +100,000 si la casa es grande y está en una buena ubicación. Esta es una interacción entre el tamaño y la ubicación, porque en este caso la diferencia en la predicción entre una casa grande y una pequeña depende de la ubicación.
Una forma de estimar la intensidad de la interacción es medir qué parte de la variación de la predicción depende de la interacción de las características. Esta medida se llama estadístico H, introducida por Friedman y Popescu (2008) 31.
5.4.2 Teoría: estadístico H de Friedman
Vamos a tratar dos casos: Primero, una medida de interacción bidireccional que nos dice si y en qué medida dos características en el modelo interactúan entre sí; segundo, una medida de interacción total que nos dice si, y en qué medida, una característica interactúa en el modelo con todas las demás características. En teoría, se pueden medir interacciones arbitrarias entre cualquier número de características, pero estos dos son los casos más interesantes.
Si dos características no interactúan, podemos descomponer la función de dependencia parcial de la siguiente manera (suponiendo que las funciones de dependencia parcial estén centradas en cero):
\[PD_{jk}(x_j,x_k)=PD_j(x_j)+PD_k(x_k)\]
donde \(PD_{jk}(x_j,x_k)\) es la función de dependencia parcial bidireccional de ambas características y \(PD_j(x_j)\) y \(PD_k(x_k)\) las funciones de dependencia parcial de las características individuales.
Del mismo modo, si una característica no tiene interacción con ninguna de las otras características, podemos expresar la función de predicción \(\hat{f}(x)\) como una suma de funciones de dependencia parcial, donde el primer sumando depende solo de j y el segundo en todas las demás funciones excepto j:
\[\hat{f}(x)=PD_j(x_j)+PD_{-j}(x_{-j})\]
donde \(PD_{-j}(x_{-j})\) es la función de dependencia parcial que depende de todas las características excepto la característica j-ésima.
Esta descomposición expresa la función de dependencia parcial (o predicción completa) sin interacciones (entre las características j y k, o respectivamente j y todas las demás características). En el siguiente paso, medimos la diferencia entre la función de dependencia parcial observada y la descompuesta sin interacciones. Calculamos la varianza de la salida de la dependencia parcial (para medir la interacción entre dos características) o de la función completa (para medir la interacción entre una característica y todas las demás características). La cantidad de la varianza explicada por la interacción (diferencia entre PD observada y sin interacción) se usa como estadística de fuerza de interacción. El estadístico es 0 si no hay interacción y 1 si toda la varianza de \(PD_{jk}\) o \(\hat{f}\) se explica por la suma de las funciones de dependencia parcial. Un estadístico 1 entre dos características significa que cada función de PD es constante y el efecto en la predicción solo se produce a través de la interacción. El estadístico H también puede ser mayor que 1, lo cual es más difícil de interpretar. Esto puede suceder cuando la varianza de la interacción bidireccional es mayor que la varianza de la gráfica de dependencia parcial bidimensional.
Matemáticamente, el estadístico H propuesto por Friedman y Popescu para la interacción entre la característica j y k es:
\[H^2_{jk}=\sum_{i=1}^n\left[PD_{jk}(x_{j}^{(i)},x_k^{(i)})-PD_j(x_j^{(i)})-PD_k(x_{k}^{(i)})\right]^2/\sum_{i=1}^n{PD}^2_{jk}(x_j^{(i)},x_k^{(i)})\]
Lo mismo se aplica para medir si una característica j interactúa con cualquier otra característica:
\[H^2_{j}=\sum_{i=1}^n\left[\hat{f}(x^{(i)})-PD_j(x_j^{(i)})-PD_{-j}(x_{-j}^{(i)})\right]^2/\sum_{i=1}^n\hat{f}^2(x^{(i)})\]
El estadístico H es costoso de evaluar, ya que itera sobre todos los puntos de datos y en cada punto se debe evaluar la dependencia parcial, que a su vez se realiza con todos los n puntos de datos. En el peor de los casos, necesitamos 2n2 llamadas a la función de predicción de modelos de aprendizaje automático para calcular el estadístico H bidireccional (j vs. k) y 3n2 para el estadístico H total (j vs. todos) Para acelerar el cálculo, podemos tomar muestras de los n puntos de datos. Esto tiene la desventaja de aumentar la varianza de las estimaciones de dependencia parcial, lo que hace que el estadístico H sea inestable. Entonces, si estás utilizando el muestreo para reducir la carga computacional, asegúrate de muestrear suficientes puntos de datos.
Friedman y Popescu también proponen una estadística de prueba para evaluar si el estadístico H difiere significativamente de cero. La hipótesis nula es la ausencia de interacción. Para generar el estadístico de interacción bajo la hipótesis nula, debes poder ajustar el modelo para que no tenga interacción entre la característica j y k o todos los demás. Esto no es posible para todos los tipos de modelos. Por lo tanto, esta prueba es específica del modelo, no es independiente del modelo y, como tal, no se trata aquí.
La estadística de fuerza de interacción también se puede aplicar en una configuración de clasificación si la predicción es una probabilidad.
5.4.3 Ejemplos
¡Veamos qué aspecto tienen las interacciones en la práctica! Medimos la fuerza de interacción de las características en una máquina de vectores de soporte que predice el número de bicicletas alquiladas en función del clima y las características de calendario. La siguiente gráfica muestra la característica de interacción H-estadística:
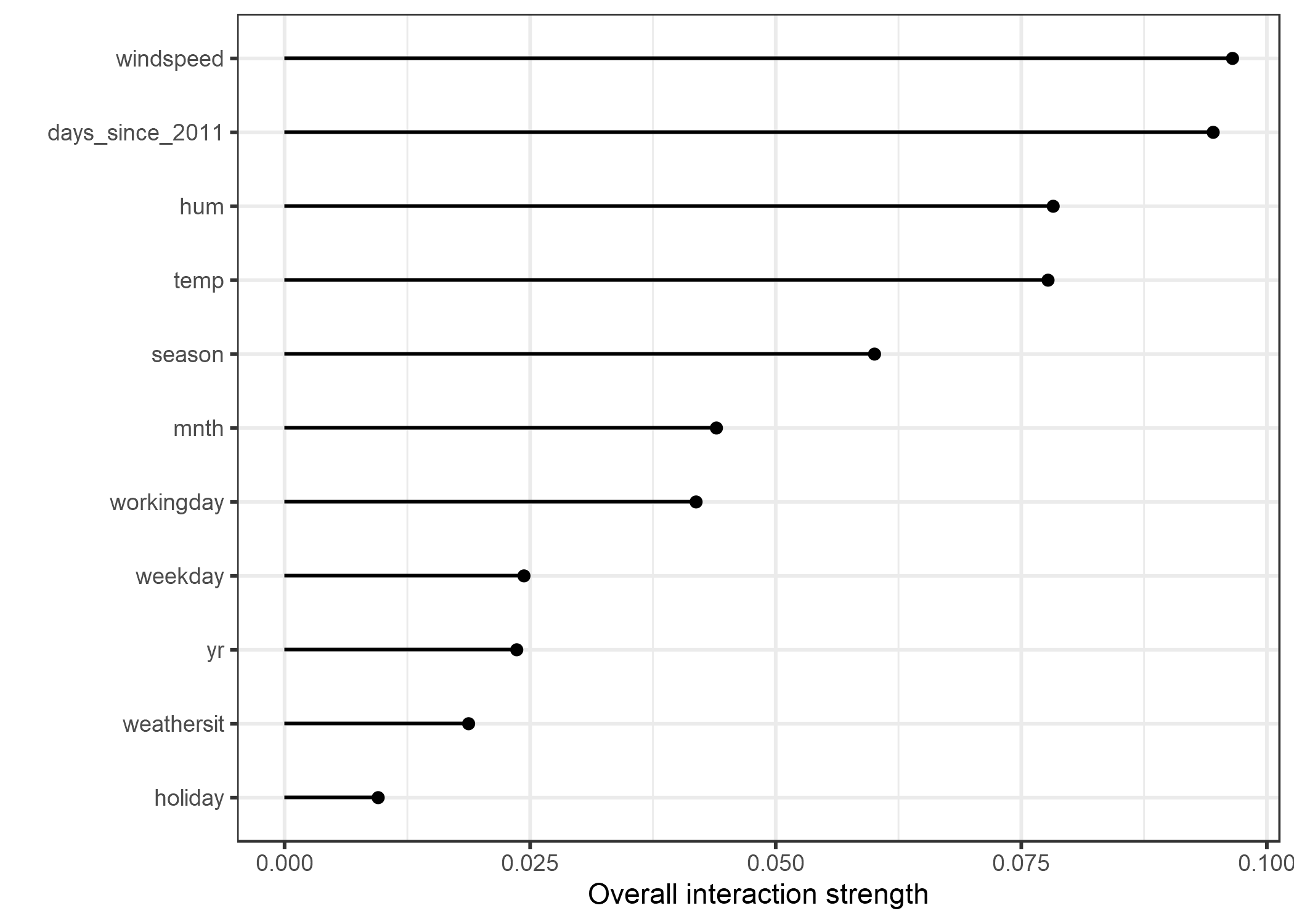
FIGURA 5.24: La fuerza de interacción (estadístico H) para cada característica con todas las demás características para una máquina de vectores de soporte que predice el alquiler de bicicletas. En general, los efectos de interacción entre las características son muy débiles (menos del 10% de la varianza explicada por característica).
En el siguiente ejemplo, calculamos la estadística de interacción para un problema de clasificación. Analizamos las interacciones entre características en un random forest entrenado para predecir cáncer cervical, dados algunos factores de riesgo.
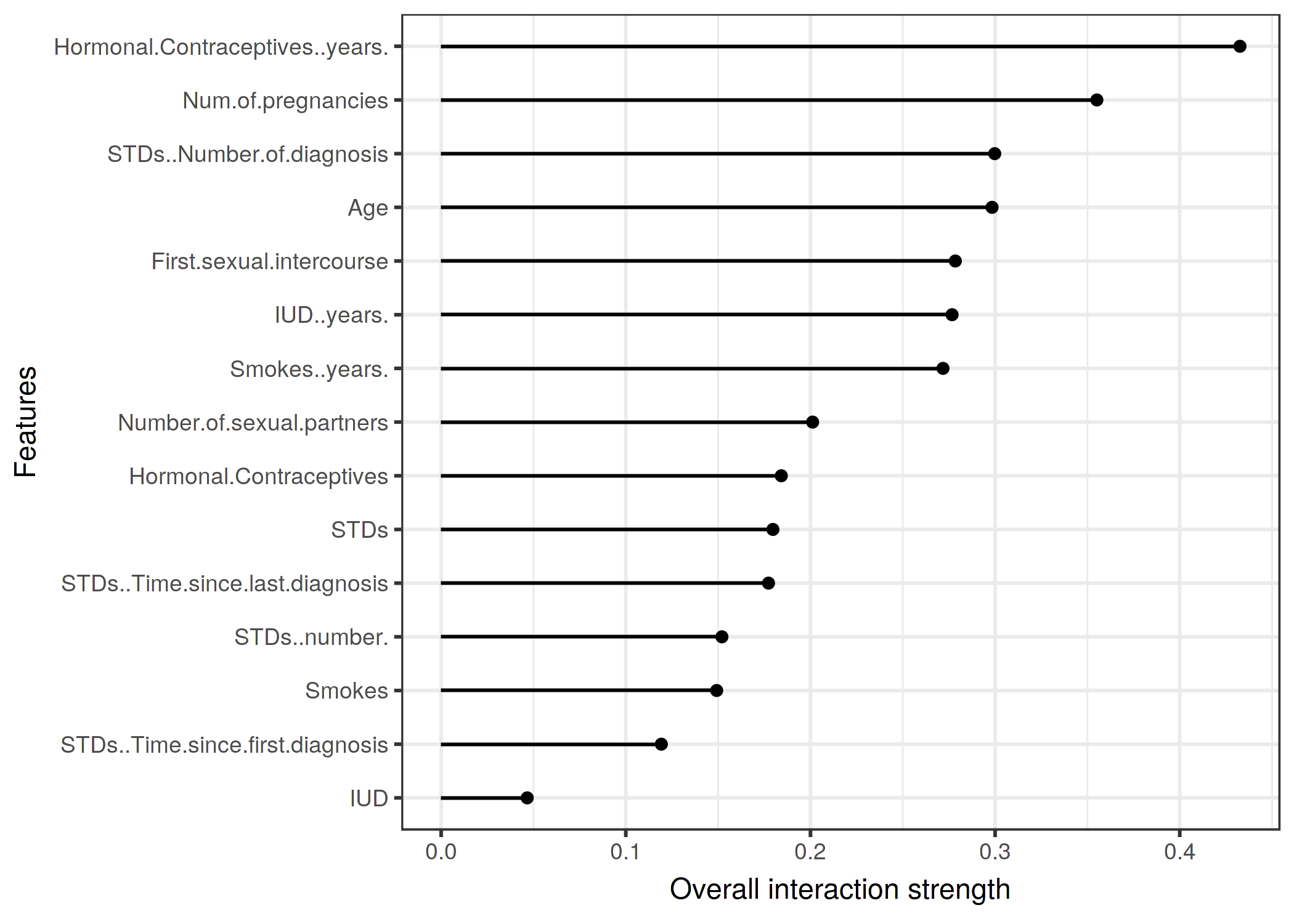
FIGURA 5.25: La fuerza de interacción (estadístico H) para cada característica con todas las demás características para un random forest que predice la probabilidad de cáncer cervical. Los años en los anticonceptivos hormonales tienen el mayor efecto de interacción relativa con todas las demás características, seguido del número de embarazos.
Después de observar las interacciones de las características de cada característica con todas las demás características, podemos seleccionar una de las características y profundizar en todas las interacciones bidireccionales entre la característica seleccionada y las otras características.
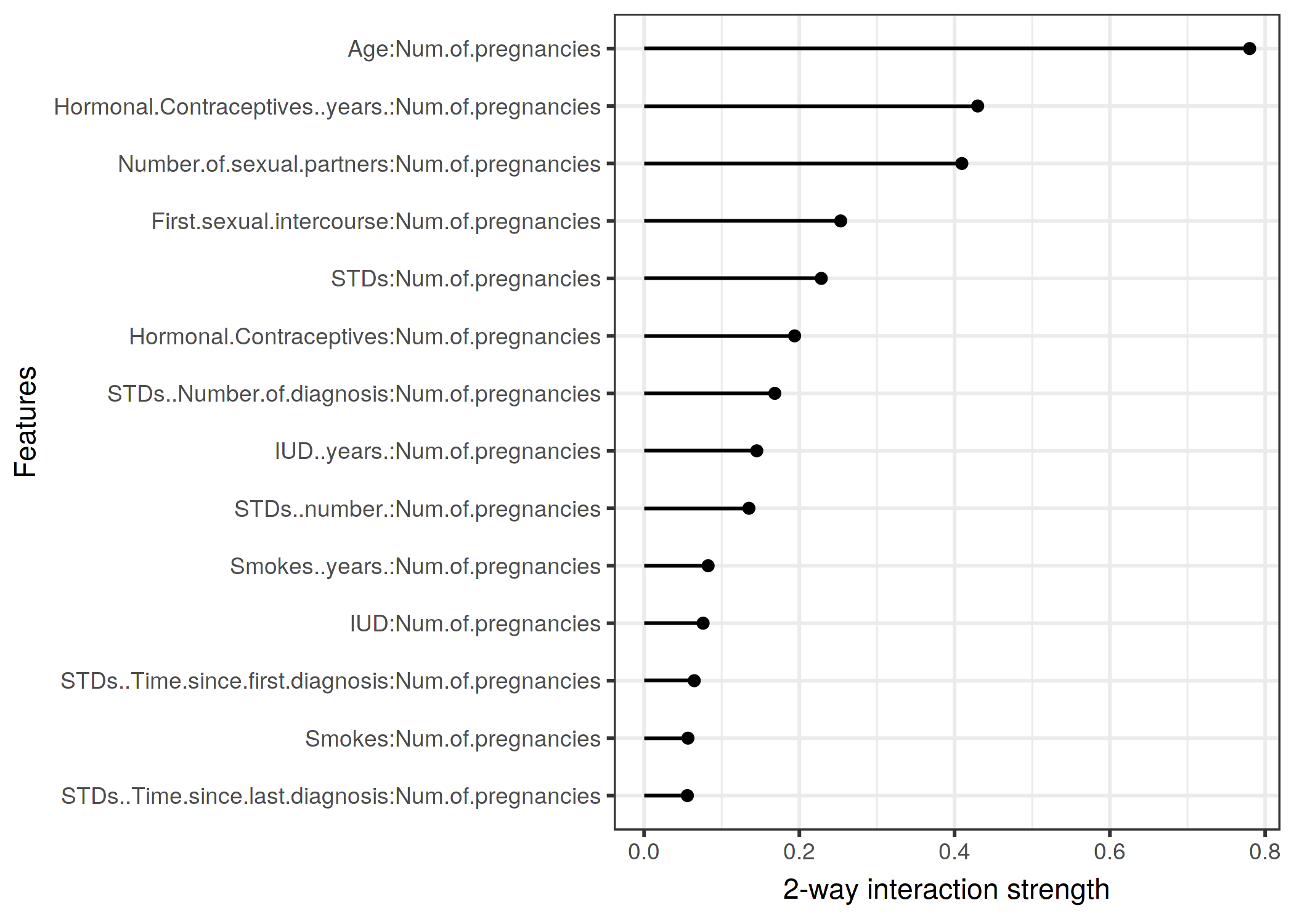
FIGURA 5.26: Las fuerzas de interacción bidimensional (Estadístico H) entre el número de embarazos y cada característica. Hay una interacción fuerte con la edad.
5.4.4 Ventajas
La interacción tiene una teoría subyacente a través de la descomposición de la dependencia parcial.
El estadístico H tiene una interpretación significativa: La interacción se define como la parte de varianza que se explica por la interacción.
Dado que el estadístico es adimensional, es comparable entre las características e incluso entre los modelos.
El estadístico detecta todo tipo de interacciones, independientemente de su forma particular.
Con el estadístico H también es posible analizar interacciones superiores arbitrarias, como la fuerza de interacción entre 3 o más características.
5.4.5 Desventajas
Lo primero que notarás: El estadístico H de interacción requiere mucho tiempo para computarse, porque es computacionalmente costoso.
El cálculo implica estimar distribuciones marginales. Estas estimaciones también tienen una cierta variación si no usamos todos los puntos de datos. Esto significa que a medida que muestreamos puntos, las estimaciones también varían de una ejecución a otra y los resultados pueden ser inestables. Recomiendo repetir el cálculo del estadístico H varias veces para ver si tiene suficientes datos para obtener un resultado estable.
No está claro si una interacción es significativamente mayor que 0. Tendríamos que realizar una prueba estadística, pero esta prueba no está (todavía) disponible en una versión independiente del modelo.
Con respecto al problema de la prueba, es difícil decir cuándo el estadístico H es lo suficientemente grande como para considerar una interacción “fuerte”.
Además, los estadísticos H pueden ser mayores que 1, lo que dificulta la interpretación.
El estadístico H nos dice la fuerza de las interacciones, pero no nos dice cómo se ven las interacciones. Para eso están las gráficos de dependencia parcial. Un flujo de trabajo significativo es medir las fortalezas de interacción y luego crear diagramas de dependencia parcial 2D para las interacciones que le interesan.
El estadístico H no se puede usar de manera significativa si las entradas son píxeles. Por lo tanto, la técnica no es útil para el clasificador de imágenes.
El estadístico de interacción funciona bajo el supuesto de que podemos barajar características de forma independiente. Si las características se correlacionan fuertemente, el supuesto se viola e integramos sobre combinaciones de características que son muy poco probables en la realidad. Ese es el mismo problema que tienen las gráficas de dependencia parcial. No se puede decir en general si conduce a una sobreestimación o subestimación.
A veces los resultados son extraños y para simulaciones pequeñas no producen los resultados esperados. Pero esto es más una observación anecdótica.
5.4.6 Implementaciones
Para los ejemplos de este libro, utilicé el paquete R iml, que está disponible en CRAN y la versión de desarrollo en Github.
Hay otras implementaciones, que se centran en modelos específicos:
El paquete R pre implementa RuleFit y H-statistic.
El paquete R gbm implementa modelos potenciados por gradiente y estadísticas H.
5.4.7 Alternativas
El estadístico H no es la única forma de medir las interacciones:
Redes de interacción variable (VIN) de Hooker (2004)32 es un enfoque que descompone la función de predicción en efectos principales e interacciones de características. Las interacciones entre las características se visualizan como una red. Lamentablemente, no hay software disponible todavía.
Dependencia parcial basada en la interacción de características de Greenwell et. al (2018)33 mide la interacción entre dos características.
Este enfoque mide la importancia de la característica (definida como la varianza de la función de dependencia parcial) de una característica condicional en diferentes puntos fijos de la otra característica.
Si la varianza es alta, entonces las características interactúan entre sí, si es cero, no interactúan.
El paquete R correspondiente vip está disponible en Github.
El paquete también cubre gráficos de dependencia parcial e importancia de la característica de permutación.
Friedman, Jerome H, and Bogdan E Popescu. “Predictive learning via rule ensembles.” The Annals of Applied Statistics. JSTOR, 916–54. (2008).↩
Hooker, Giles. “Discovering additive structure in black box functions.” Proceedings of the tenth ACM SIGKDD international conference on Knowledge discovery and data mining. (2004).↩
Greenwell, Brandon M., Bradley C. Boehmke, and Andrew J. McCarthy. “A simple and effective model-based variable importance measure.” arXiv preprint arXiv:1805.04755 (2018).↩