6.4 Instancias influyentes

Los modelos de aprendizaje automático son, en última instancia, un producto de datos de entrenamiento y la eliminación de una de las instancias de entrenamiento puede afectar el modelo resultante. Llamamos a una instancia de entrenamiento “influyente” cuando su eliminación de los datos de entrenamiento cambia considerablemente los parámetros o predicciones del modelo. Al identificar instancias de entrenamiento influyentes, podemos “depurar” los modelos de aprendizaje automático y explicar mejor sus comportamientos y predicciones.

Este capítulo te muestra dos enfoques para identificar instancias influyentes, a saber, diagnósticos de eliminación y funciones de influencia. Ambos enfoques se basan en estadísticas sólidas, que proporcionan métodos estadísticos que se ven menos afectados por valores atípicos o violaciones de los supuestos del modelo. Las estadísticas robustas también proporcionan métodos para medir qué tan robustas son las estimaciones de los datos (como una estimación media o los pesos de un modelo de predicción).

Imagina que deseas estimar el ingreso promedio de las personas en tu ciudad y preguntar a diez personas aleatorias en la calle cuánto ganan. Además del hecho de que tu muestra probablemente sea realmente mala, ¿cuánto puede influir la estimación de ingresos promedio por una sola persona? Para responder a esta pregunta, puedes volver a calcular el valor medio omitiendo respuestas individuales o derivar matemáticamente a través de “funciones de influencia” cómo se puede influir en el valor medio. Con el enfoque de eliminación, recalculamos el valor medio diez veces, omitiendo uno de los estados de resultados cada vez y medimos cuánto cambia la estimación media. Un gran cambio significa que una instancia fue muy influyente. El segundo enfoque pondera a una de las personas en un peso infinitesimalmente pequeño, que corresponde al cálculo de la primera derivada de una estadística o modelo. Este enfoque también se conoce como “enfoque infinitesimal” o “función de influencia”. La respuesta es, por cierto, que la estimación media puede estar muy influenciada por una sola respuesta, ya que la media se escala linealmente con valores únicos. Una opción más sólida es la mediana (el valor en el que la mitad de las personas gana más y la otra mitad menos), porque incluso si la persona con el ingreso más alto en su muestra ganara diez veces más, la mediana resultante no cambiaría.

Los diagnósticos de eliminación y las funciones de influencia también se pueden aplicar a los parámetros o predicciones de los modelos de aprendizaje automático para comprender mejor su comportamiento o explicar predicciones individuales. Antes de analizar estos dos enfoques para encontrar instancias influyentes, examinaremos la diferencia entre una instancia atípica y una instancia influyente.

Valores atípicos

Un valor atípico es una instancia que está muy lejos de las otras instancias del conjunto de datos. “Lejos” significa que la distancia, por ejemplo euclidiana, es muy grande. En un conjunto de datos de recién nacidos, un recién nacido que pesa 6 kg se consideraría un valor atípico. En un conjunto de datos de cuentas bancarias con cuentas corrientes en su mayoría, una cuenta de préstamo dedicada (saldo negativo grande, pocas transacciones) se consideraría un valor atípico. La siguiente figura muestra un valor atípico para una distribución unidimensional.

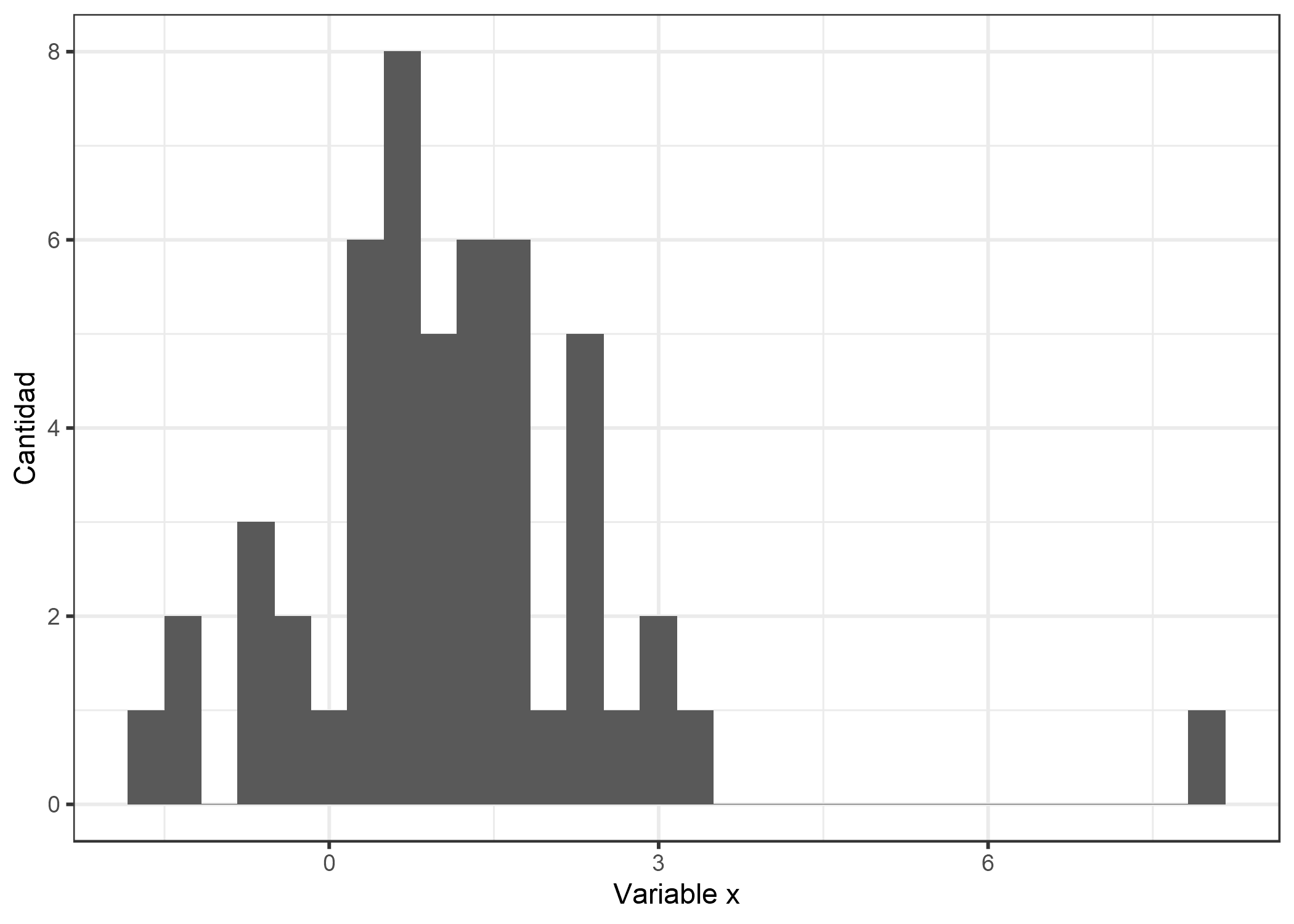
FIGURA 6.14: La variable x sigue una distribución gaussiana con un valor atípico en x = 8.

Los valores atípicos pueden ser puntos de datos interesantes (por ejemplo, excepciones). Cuando un valor atípico influye en el modelo, también es una instancia influyente.

Instancias influyentes

Una instancia influyente es una instancia de datos cuya eliminación tiene un fuerte efecto en el modelo entrenado. Cuanto más cambien los parámetros o predicciones del modelo cuando el modelo se vuelva a entrenar con una instancia particular eliminada de los datos de entrenamiento, más influyente será esa instancia. Si una instancia es influyente para un modelo entrenado también depende de su valor para el objetivo y. La siguiente figura muestra una instancia influyente para un modelo de regresión lineal.

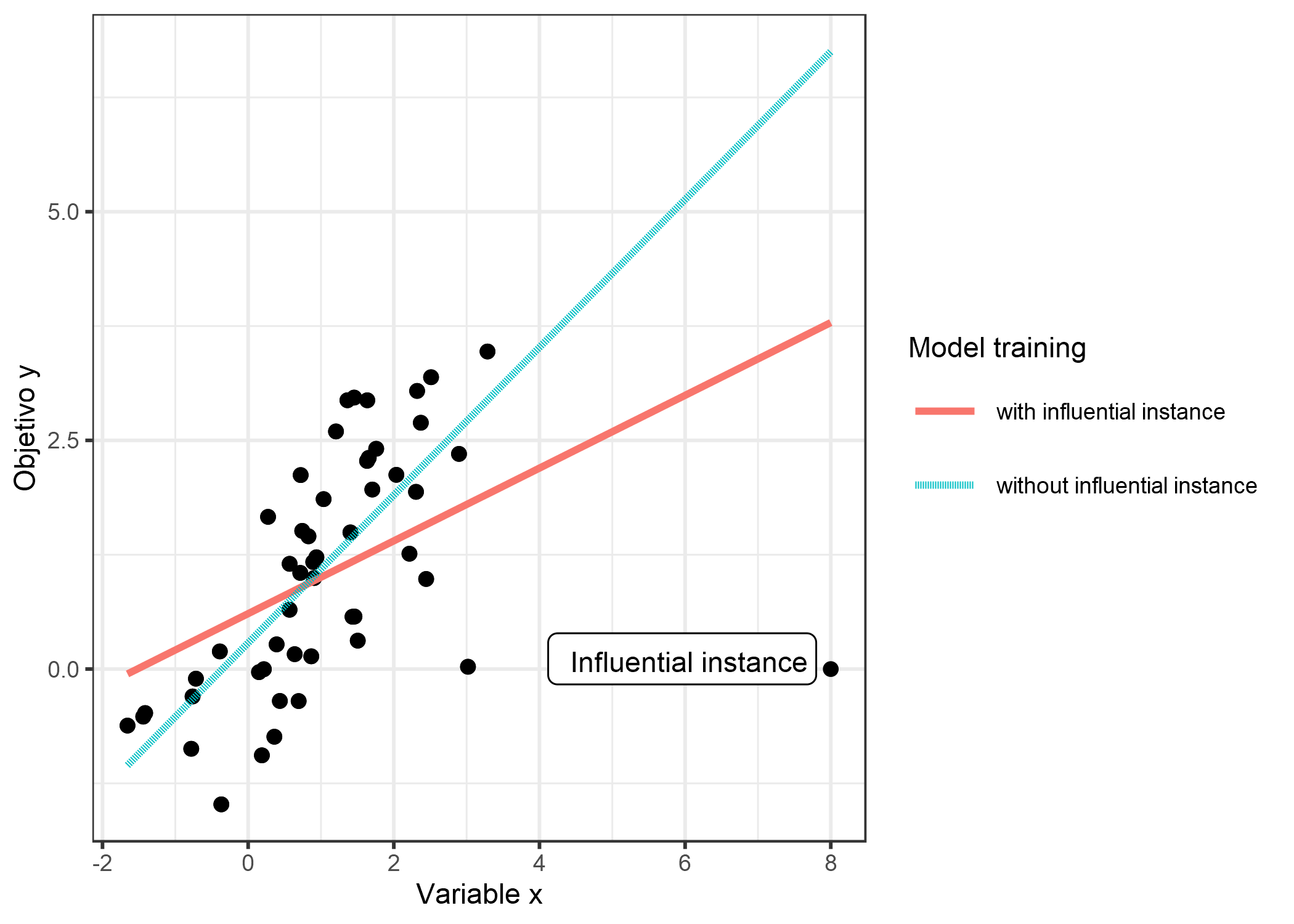
FIGURA 6.15: Un modelo lineal con una característica. Entrenado una vez en los datos completos y una vez sin la instancia influyente. Eliminar la instancia influyente cambia drásticamente la pendiente ajustada (peso / coeficiente).

¿Por qué las instancias influyentes ayudan a entender el modelo?

La idea clave detrás de las instancias influyentes para la interpretabilidad es rastrear los parámetros y predicciones del modelo hasta donde comenzó todo: los datos de entrenamiento. Un alumno, es decir, el algoritmo que genera el modelo de aprendizaje automático, es una función que toma datos de entrenamiento que constan de las características X y el objetivo Y y genera un modelo de aprendizaje automático. Por ejemplo, el alumno de un árbol de decisión es un algoritmo que selecciona las características divididas y los valores en los que se divide. Un alumno para una red neuronal utiliza la propagación hacia atrás para encontrar los mejores pesos.

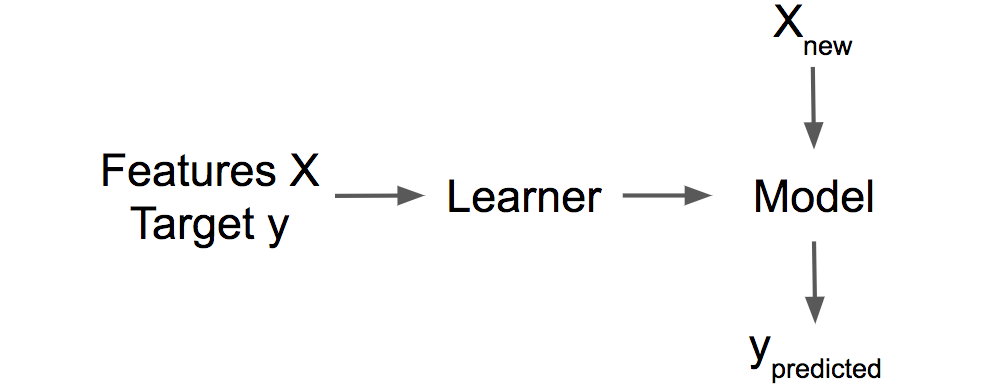
FIGURA 6.16: Un alumno aprende un modelo a partir de datos de entrenamiento (características más objetivo). El modelo hace predicciones para nuevos datos.

Preguntamos cómo cambiarían los parámetros del modelo o las predicciones si eliminamos instancias de entrenamiento en el proceso de entrenamiento. Esto contrasta con otros enfoques de interpretabilidad que analizan cómo cambia la predicción cuando manipulamos las características de las instancias a predecir, como gráficos de dependencia parcial o importancia de la característica. Con instancias influyentes, no tratamos el modelo como fijo, sino como una función de los datos de entrenamiento. Las instancias influyentes nos ayudan a responder preguntas sobre el comportamiento del modelo global y las predicciones individuales. ¿Cuáles fueron las instancias más influyentes para los parámetros del modelo o las predicciones en general? ¿Cuáles fueron las instancias más influyentes para una predicción particular? Las instancias influyentes nos dicen para qué instancias el modelo podría tener problemas, qué instancias de entrenamiento deberían verificarse en busca de errores y dar una impresión de la solidez del modelo. Es posible que no confiemos en un modelo si una sola instancia tiene una fuerte influencia en las predicciones y parámetros del modelo. Al menos eso nos haría investigar más a fondo.

¿Cómo podemos encontrar instancias influyentes? Tenemos dos formas de medir la influencia: Nuestra primera opción es eliminar la instancia de los datos de entrenamiento, volver a entrenar el modelo en el conjunto de datos de entrenamiento reducido y observar la diferencia en los parámetros o predicciones del modelo (individualmente o sobre el conjunto de datos completo). La segunda opción es aumentar el peso de una instancia de datos aproximando los cambios de parámetros en función de los gradientes de los parámetros del modelo. El enfoque de eliminación es más fácil de entender y motiva el enfoque de mejora, por lo que comenzamos con el primero.

6.4.1 Diagnóstico de eliminación

Los estadísticos ya han investigado mucho en el área de instancias influyentes, especialmente para los modelos de regresión lineal (generalizados). Cuando busca “observaciones influyentes”, los primeros resultados de búsqueda se refieren a medidas como DFBETA y la distancia de Cook. DFBETA mide el efecto de eliminar una instancia en los parámetros del modelo. La distancia de Cook (Cook, 1977⁵⁸) mide el efecto de eliminar una instancia en las predicciones del modelo. Para ambas medidas tenemos que volver a entrenar el modelo repetidamente, omitiendo instancias individuales cada vez. Los parámetros o predicciones del modelo con todas las instancias se comparan con los parámetros o predicciones del modelo con una de las instancias eliminadas de los datos de entrenamiento.

DFBETA se define como:

\[DFBETA_{i}=\beta-\beta^{(-i)}\]

donde \(\beta\) es el vector de peso cuando el modelo se entrena en todas las instancias de datos, y \(\beta^{(-i)}\) el vector de peso cuando el modelo se entrena sin instancia i. Muy intuitivo, dirías. DFBETA funciona solo para modelos con parámetros de peso, como regresión logística o redes neuronales, pero no para modelos como árboles de decisión, conjuntos de árboles, algunas máquinas de vectores de soporte, etc.

La distancia de Cook se inventó para los modelos de regresión lineal y existen aproximaciones para los modelos de regresión lineal generalizados. La distancia de Cook para una instancia de entrenamiento se define como la suma (a escala) de las diferencias al cuadrado en el resultado predicho cuando la i-ésima instancia se elimina del modelo de entrenamiento.

\[D_i=\frac{\sum_{j=1}^n(\hat{y}_j-\hat{y}_{j}^{(-i)})^2}{p\cdot{}MSE}\]

donde el numerador es la diferencia al cuadrado entre la predicción del modelo con y sin la i-ésima instancia, sumada sobre el conjunto de datos. El denominador es el número de características p veces el error cuadrático medio. El denominador es el mismo para todas las instancias, sin importar qué instancia se elimine. La distancia de Cook nos dice cuánto cambia la salida predicha de un modelo lineal cuando eliminamos la i-ésima instancia del entrenamiento.

¿Podemos usar la distancia de Cook y DFBETA para cualquier modelo de aprendizaje automático? DFBETA requiere parámetros de modelo, por lo que esta medida solo funciona para modelos parametrizados. La distancia de Cook no requiere ningún parámetro del modelo. Curiosamente, la distancia de Cook generalmente no se ve fuera del contexto de los modelos lineales y los modelos lineales generalizados, pero la idea de tomar la diferencia entre las predicciones del modelo antes y después de la eliminación de una instancia particular es muy general. Un problema con la definición de la distancia de Cook es el MSE, que no es significativo para todos los tipos de modelos de predicción (por ejemplo, clasificación).

La medida de influencia más simple para el efecto en las predicciones del modelo se puede escribir de la siguiente manera:

\[\text{Influence}^{(-i)}=\frac{1}{n}\sum_{j=1}^{n}\left|\hat{y}_j-\hat{y}_{j}^{(-i)}\right|\]

Esta expresión es básicamente el numerador de la distancia de Cook, con la diferencia de que la diferencia absoluta se suma en lugar de las diferencias al cuadrado. Esta fue una elección que hice, porque tiene sentido para los ejemplos posteriores. La forma general de las medidas de diagnóstico de eliminación consiste en elegir una medida (como el resultado pronosticado) y calcular la diferencia de la medida para el modelo entrenado en todas las instancias y cuando se elimina la instancia.

Podemos desglosar fácilmente la influencia para explicar para la predicción de la instancia j cuál fue la influencia de la i-ésima instancia de entrenamiento:

\[\text{Influence}_{j}^{(-i)}=\left|\hat{y}_j-\hat{y}_{j}^{(-i)}\right|\]

Esto también funcionaría para la diferencia en los parámetros del modelo o la diferencia en la pérdida. En el siguiente ejemplo usaremos estas simples medidas de influencia.

Ejemplo de diagnóstico de eliminación

En el siguiente ejemplo, entrenamos una SVM para predecir cáncer cervical dados los factores de riesgo y medir qué instancias de entrenamiento fueron más influyentes en general y para una predicción particular. Dado que la predicción del cáncer es un problema de clasificación, medimos la influencia como la diferencia en la probabilidad pronosticada de cáncer. Una instancia es influyente si la probabilidad pronosticada aumenta o disminuye en promedio en el conjunto de datos cuando la instancia se elimina del entrenamiento del modelo. La medición de la influencia para todas las instancias de entrenamiento 858 requiere entrenar el modelo una vez en todos los datos y volver a entrenarlo 858 veces (= tamaño de los datos de entrenamiento) con una de las instancias eliminadas hora.

La instancia más influyente tiene una medida de influencia de aproximadamente 0.01. Una influencia de 0.01 significa que si eliminamos la instancia 540, la probabilidad pronosticada cambia en 1 punto porcentual en promedio. Esto es bastante considerable teniendo en cuenta que la probabilidad pronosticada promedio de cáncer es 6.4%. El valor medio de las medidas de influencia sobre todas las eliminaciones posibles es 0.2 puntos porcentuales. Ahora sabemos cuáles de las instancias de datos fueron más influyentes para el modelo. Esto ya es útil para depurar los datos. ¿Hay alguna instancia problemática? ¿Hay errores de medición? Las instancias influyentes son las primeras que deben verificarse en busca de errores, porque cada error en ellas influye fuertemente en las predicciones del modelo.

Además de la depuración del modelo, ¿podemos aprender algo para comprender mejor el modelo? Simplemente imprimir las 10 instancias más influyentes no es muy útil, porque es solo una tabla de instancias con muchas características. Todos los métodos que devuelven instancias como salida solo tienen sentido si tenemos una buena manera de representarlos. Pero podemos entender mejor qué tipo de instancias influyen cuando preguntamos: ¿Qué distingue una instancia influyente de una instancia no influyente? Podemos convertir esta pregunta en un problema de regresión y modelar la influencia de una instancia en función de sus valores característicos. Somos libres de elegir cualquier modelo del capítulo sobre Modelos de aprendizaje automático interpretables. Para este ejemplo, elegí un árbol de decisión (figura siguiente) que muestra que los datos de mujeres de 35 años o más fueron los más influyentes para la máquina de vectores de soporte. De todas las mujeres en el conjunto de datos 153 de 858 tenían más de 35 años. En el capítulo sobre Gráficos de dependencia parcial, hemos visto que después de 40 hay un fuerte aumento en la probabilidad pronosticada de cáncer y la [Importancia de la característica] (#importanciadecaracteristicas) también ha detectado la edad como uno de las características más importantes. El análisis de influencia nos dice que el modelo se vuelve cada vez más inestable al predecir el cáncer para edades más altas. Esto en sí mismo es información valiosa. Esto significa que los errores en estos casos pueden tener un fuerte efecto en el modelo.

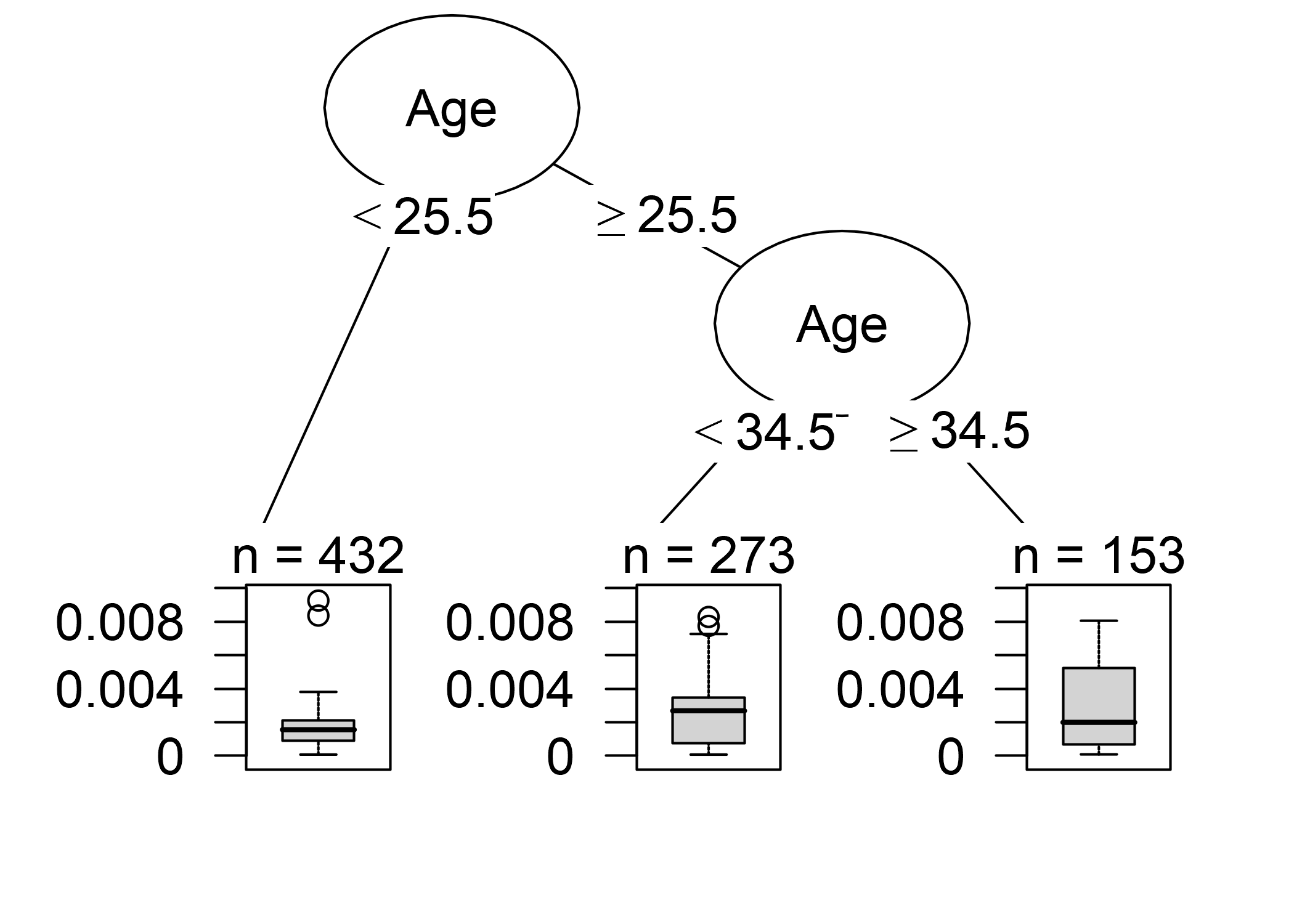
FIGURA 6.17: Un árbol de decisión que modela la relación entre la influencia de las instancias y sus características. La profundidad máxima del árbol se establece en 2.

Este primer análisis de influencia reveló la instancia general más influyente. Ahora seleccionamos una de las instancias, a saber, la instancia número 7, para la que queremos explicar la predicción al encontrar las instancias de datos de entrenamiento más influyentes. Es como una pregunta contrafactual: ¿Cómo cambiaría la predicción por ejemplo 7 si omitimos la instancia i del proceso de entrenamiento? Repetimos esta eliminación para todas las instancias. Luego seleccionamos las instancias de entrenamiento que resultan en el mayor cambio en la predicción de la instancia 7 cuando se omiten del entrenamiento y las usamos para explicar la predicción del modelo para esa instancia. Elegí explicar la predicción, por ejemplo, 7 porque es la instancia con la mayor probabilidad pronosticada de cáncer (7.35%), que pensé fue un caso interesante para analizar más profundamente. Podríamos devolver, por ejemplo, las 10 instancias más influyentes para predecir la instancia número 7 impresa como una tabla. No es muy útil, porque no pudimos ver mucho. Nuevamente, tiene más sentido descubrir qué distingue las instancias influyentes de las instancias no influyentes analizando sus características. Usamos un árbol de decisión entrenado para predecir la influencia dadas las características, pero en realidad lo usamos mal solo para encontrar una estructura y no para predecir algo. El siguiente árbol de decisión muestra qué tipo de instancias de entrenamiento fueron más influyentes para predecir la instancia 7.

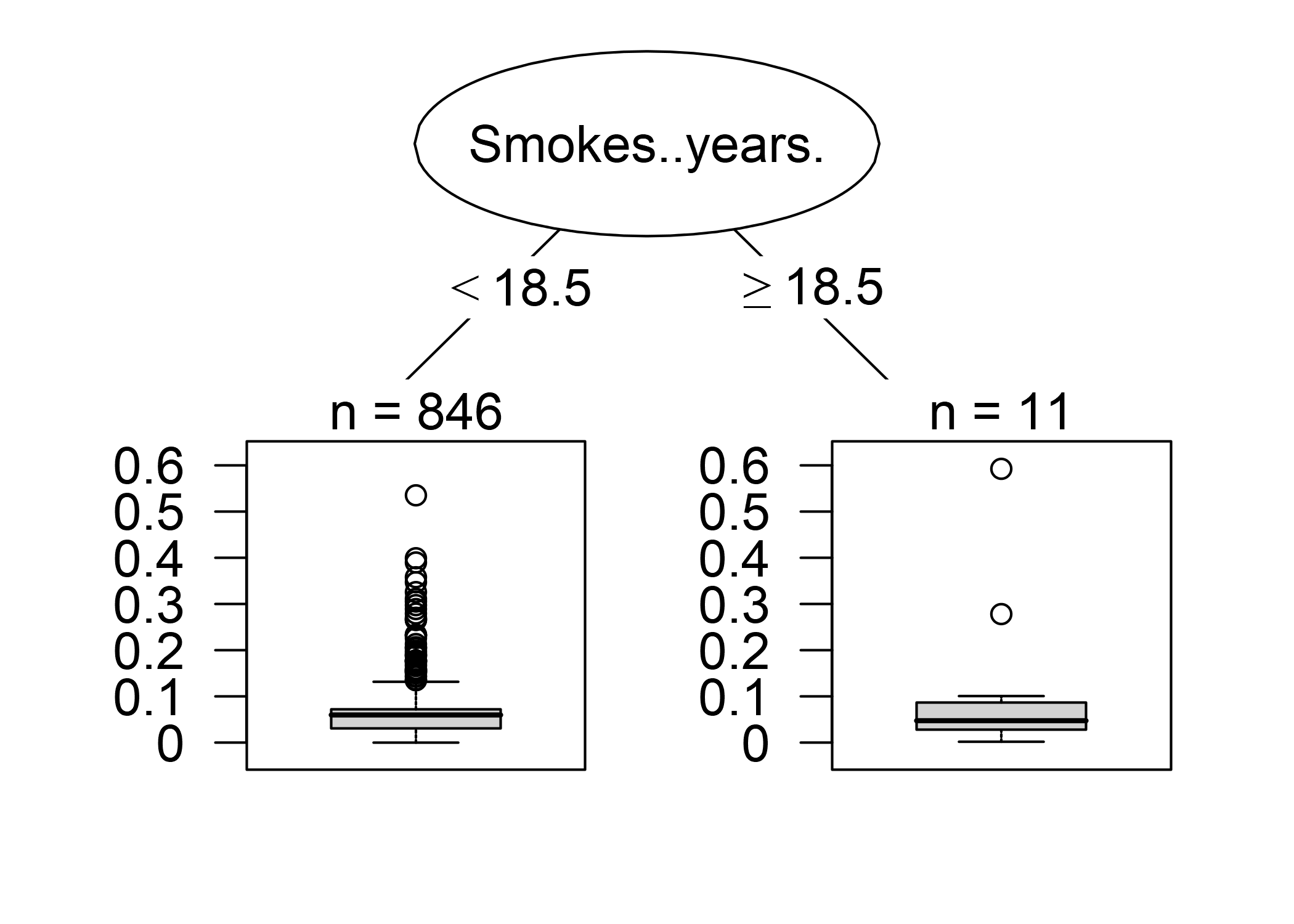
FIGURA 6.18: Árbol de decisión que explica qué instancias fueron más influyentes para predecir la 7-ésima instancia. Los datos de mujeres que fumaron durante 18.5 años o más tuvieron una gran influencia en el predicción de la 7-ésima instancia, con un cambio promedio en la predicción absoluta en 11.7 puntos porcentuales de probabilidad de cáncer

Las instancias de datos de mujeres que fumaron o han estado fumando durante 18.5 años o más tienen una gran influencia en la predicción de la 7-ésima instancia. La mujer detrás de la 7 instancia fumaba por 34 años. En los datos, 12 mujeres (1.40%) fumaron 18.5 años o más. Cualquier error cometido en la recolección del número de años de fumar de una de estas mujeres tendrá un gran impacto en el resultado previsto para la 7-ésima instancia.

El cambio más extremo en la predicción ocurre cuando eliminamos el número de instancia 663. El paciente supuestamente fumó por 22 años, alineado con los resultados del árbol de decisiones. La probabilidad predicha para la 7-ésima instancia cambia de 7.35% a 66.60% si eliminamos la instancia 663!

Si observamos más de cerca las características de la instancia más influyente, podemos ver otro posible problema. Los datos dicen que la mujer tiene 28 años y ha estado fumando durante 22 años. O es un caso realmente extremo y ella realmente comenzó a fumar a los 6, o esto es un error de datos. Tiendo a creer lo último. Esta es ciertamente una situación en la que debemos cuestionar la precisión de los datos.

Estos ejemplos mostraron lo útil que es identificar instancias influyentes para depurar modelos. Un problema con el enfoque propuesto es que el modelo necesita ser reentrenado para cada instancia de entrenamiento. Todo el reentrenamiento puede ser bastante lento, porque si tienes miles de instancias de entrenamiento, tendrás que reentrenar tu modelo miles de veces. Suponiendo que el modelo demore un día en entrenarse y que tenga 1000 instancias de entrenamiento, el cálculo de instancias influyentes, sin paralelización, tomará casi 3 años. Nadie tiene tiempo para esto. En el resto de este capítulo, te mostraré un método que no requiere volver a entrenar el modelo.

6.4.2 Funciones de influencia

Tú: Quiero saber la influencia que tiene una instancia de entrenamiento en una predicción particular.
Investigación: puede eliminar la instancia de entrenamiento, volver a entrenar el modelo y medir la diferencia en la predicción.
Tú:¡Genial! ¿Pero tienes un método para mí que funcione sin reentrenamiento? Toma mucho tiempo
Investigación: ¿Tiene un modelo con una función de pérdida que sea dos veces diferenciable con respecto a sus parámetros?
Tú: Entrené una red neuronal con la pérdida logística. Entonces sí.
Investigación : Entonces, puede aproximar la influencia de la instancia en los parámetros del modelo y en la predicción con funciones de influencia.
La función de influencia es una medida de cuán fuertemente dependen los parámetros o predicciones del modelo de una instancia de entrenamiento.
En lugar de eliminar la instancia, el método compensa la instancia en la pérdida en un paso muy pequeño.
Este método implica aproximar la pérdida alrededor de los parámetros del modelo actual usando el gradiente y la matriz de Hesse.
La pérdida de peso es similar a eliminar la instancia.
Tú: Genial, ¡eso es lo que estoy buscando!

Koh y Liang (2017)⁵⁹ sugirieron usar funciones de influencia, un método de estadísticas robustas, para medir cómo una instancia influye en los parámetros o predicciones del modelo. Al igual que con los diagnósticos de eliminación, las funciones de influencia rastrean los parámetros y predicciones del modelo hasta la instancia de entrenamiento responsable. Sin embargo, en lugar de eliminar instancias de entrenamiento, el método se aproxima a cuánto cambia el modelo cuando la instancia se compensa en el riesgo empírico (suma de la pérdida sobre los datos de entrenamiento).

El método de las funciones de influencia requiere acceso al gradiente de pérdida con respecto a los parámetros del modelo, que solo funciona para un subconjunto de modelos de aprendizaje automático. La regresión logística, las redes neuronales y las máquinas de vectores de soporte califican, los métodos basados en árboles como los random forest no. Las funciones de influencia ayudan a comprender el comportamiento del modelo, depurar el modelo y detectar errores en el conjunto de datos.

La siguiente sección explica la intuición y las matemáticas detrás de las funciones de influencia.

Matemáticas detrás de las funciones de influencia

La idea clave detrás de las funciones de influencia es aumentar la pérdida de una instancia de entrenamiento mediante un paso infinitesimalmente pequeño \(\epsilon\), que da como resultado nuevos parámetros del modelo:

\[\hat{\theta}_{\epsilon,z}=\arg\min_{\theta{}\in\Theta}(1-\epsilon)\frac{1}{n}\sum_{i=1}^n{}L(z_i,\theta)+\epsilon{}L(z,\theta)\]

donde \(\theta\) es el vector de parámetros del modelo y \(\hat{\theta}_{\epsilon,z}\) es el vector de parámetros después de aumentar z por un número muy pequeño \(\epsilon\). L es la función de pérdida con la que se entrenó el modelo, \(z_i\) son los datos de entrenamiento y z es la instancia de entrenamiento que queremos aumentar para simular su eliminación. La intuición detrás de esta fórmula es: ¿Cuánto cambiará la pérdida si aumentamos un poco de peso una instancia particular \(z_i\) de los datos de entrenamiento (\(\epsilon\)) y atenuamos las otras instancias de datos en consecuencia? ¿Cómo sería el vector de parámetros para optimizar esta nueva pérdida combinada? La función de influencia de los parámetros, es decir, la influencia de la instancia de entrenamiento de ponderación z sobre los parámetros, se puede calcular de la siguiente manera.

\[I_{\text{up,params}}(z)=\left.\frac{d{}\hat{\theta}_{\epsilon,z}}{d\epsilon}\right|_{\epsilon=0}=-H_{\hat{\theta}}^{-1}\nabla_{\theta}L(z,\hat{\theta})\]

La última expresión \(\nabla_{\theta}L(z,\hat{\theta})\) es el gradiente de pérdida con respecto a los parámetros para la instancia de entrenamiento ponderada. El gradiente es la tasa de cambio de la pérdida de la instancia de entrenamiento. Nos dice cuánto cambia la pérdida cuando cambiamos un poco los parámetros del modelo \(\hat{\theta}\). Una entrada positiva en el vector gradiente significa que un pequeño aumento en el parámetro del modelo correspondiente aumenta la pérdida, una entrada negativa significa que el aumento del parámetro reduce la pérdida. La primera parte \(H^{-1}_{\hat{\theta}}\) es la matriz Hessiana inversa (segunda derivada de la pérdida con respecto a los parámetros del modelo). La matriz Hessiana es la tasa de cambio del gradiente, o expresada como pérdida, es la tasa de cambio de la tasa de cambio de la pérdida. Se puede estimar usando:

\[H_{\theta}=\frac{1}{n}\sum_{i=1}^n\nabla^2_{\hat{\theta}}L(z_i,\hat{\theta})\]

Más informalmente: La matriz de Hesse registra cuán curvada es la pérdida en cierto punto. El Hessiano es una matriz y no solo un vector, porque describe la curvatura de la pérdida y la curvatura depende de la dirección en la que miremos. El cálculo real del Hessiano lleva mucho tiempo si tiene muchos parámetros. Koh y Liang sugirieron algunos trucos para calcularlo de manera eficiente, lo que va más allá del alcance de este capítulo. Actualizar los parámetros del modelo, como se describe en la fórmula anterior, es equivalente a dar un solo paso de Newton después de formar una expansión cuadrática alrededor de los parámetros estimados del modelo.

¿Qué intuición hay detrás de esta fórmula de función de influencia? La fórmula proviene de formar una expansión cuadrática alrededor de los parámetros \(\hat{\theta}\). Eso significa que en realidad no lo sabemos, o es demasiado complejo calcular cómo cambiará exactamente la pérdida de instancia z cuando se elimine/aumente. Aproximamos la función localmente mediante el uso de información sobre la inclinación (= gradiente) y la curvatura (= matriz de Hesse) en la configuración del parámetro del modelo actual. Con esta aproximación de pérdida, podemos calcular cómo se verían aproximadamente los nuevos parámetros si ponderamos la instancia z:

\[\hat{\theta}_{-z}\approx\hat{\theta}-\frac{1}{n}I_{\text{up,params}}(z)\]

El vector de parámetro aproximado es básicamente el parámetro original menos el gradiente de la pérdida de z (porque queremos disminuir la pérdida) escalado por la curvatura (= multiplicado por la matriz Hessiana inversa) y escalado por 1 sobre n, porque ese es la peso de una sola instancia de entrenamiento.

La siguiente figura muestra cómo funciona el aumento de peso. El eje x muestra el valor del parámetro \(\theta\) y el eje y el valor correspondiente de la pérdida con instancia ponderada z. El parámetro modelo aquí es unidimensional para fines de demostración, pero en realidad suele ser de alta dimensión. Nos movemos solo 1 sobre n en la dirección de mejora de la pérdida, por ejemplo z. No sabemos cómo cambiaría realmente la pérdida cuando eliminamos z, pero con la primera y segunda derivada de la pérdida, creamos esta aproximación cuadrática alrededor de nuestro parámetro de modelo actual y pretendemos que así es como se comportaría la pérdida real.

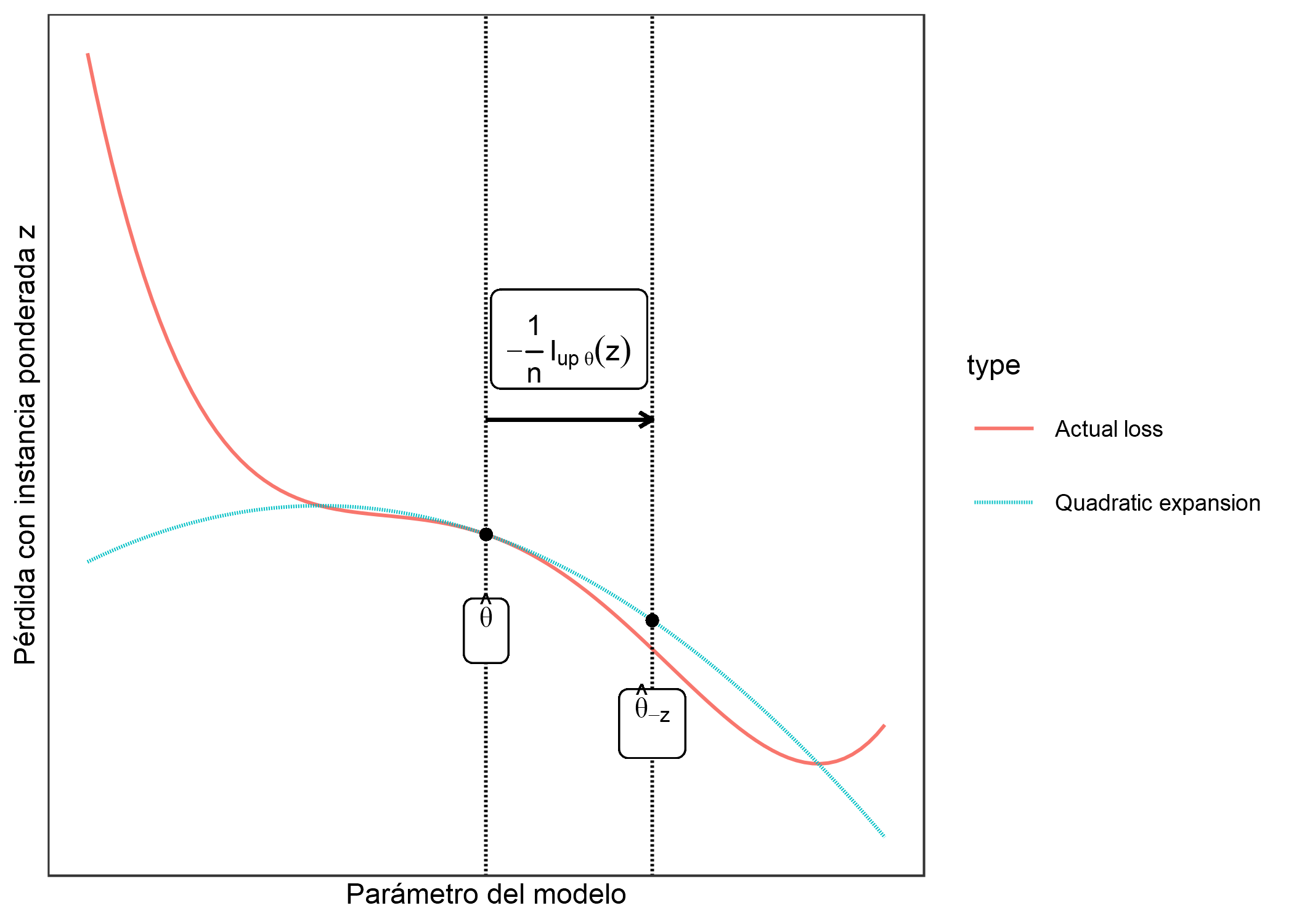
FIGURA 6.19: Actualizando el parámetro del modelo (eje x) formando una expansión cuadrática de la pérdida alrededor del parámetro del modelo actual, y moviendo 1/n en la dirección en que la pérdida con la instancia ponderada z (eje y) mejora más. Esta ponderación de la instancia z en la pérdida se aproxima a los cambios de parámetros si eliminamos z y entrenamos el modelo en los datos reducidos.

En realidad, no necesitamos calcular los nuevos parámetros, pero podemos usar la función de influencia como una medida de la influencia de z en los parámetros.

¿Cómo cambian las predicciones cuando aumentamos de peso la instancia de entrenamiento z? Podemos calcular los nuevos parámetros y luego hacer predicciones usando el modelo recién parametrizado, o también podemos calcular la influencia de la instancia z en las predicciones directamente, ya que podemos calcular la influencia usando la regla de la cadena:

\[\begin{align*}I_{up,loss}(z,z_{test})&=\left.\frac{d{}L(z_{test},\hat{\theta}_{\epsilon,z})}{d\epsilon}\right|_{\epsilon=0}\\&=\left.\nabla_{\theta}L(z_{test},\hat{\theta})^T\frac{d\hat{\theta}_{\epsilon,z}}{d\epsilon}\right|_{\epsilon=0}\\&=-\nabla_{\theta}L(z_{test},\hat{\theta})^T{}H^{-1}_{\theta}\nabla_{\theta}L(z,\hat{\theta})\end{align*}\]

La primera línea de esta ecuación significa que medimos la influencia de una instancia de entrenamiento en una determinada predicción \(z_ {test}\) como un cambio en la pérdida de la instancia de prueba cuando aumentamos la instancia z y obtenemos nuevos parámetros \(\hat{\theta}_{\epsilon,z}\). Para la segunda línea de la ecuación, hemos aplicado la regla de la cadena de derivados y obtenemos la derivada de la pérdida de la instancia de prueba con respecto a los parámetros multiplicados por la influencia de z en los parámetros. En la tercera línea, reemplazamos la expresión con la función de influencia para los parámetros. El primer término en la tercera línea \(\nabla_{\theta}L(z_{test},\hat{\theta})^T{}\) es el gradiente de la instancia de prueba con respecto a los parámetros del modelo.

Tener una fórmula es excelente y la forma científica y precisa de mostrar las cosas. Pero creo que es muy importante hacerse una idea de lo que significa la fórmula. La fórmula para \(I_{\text{up,loss}}\) establece que la función de influencia de la instancia de entrenamiento z en la predicción de una instancia \(z_{test}\) es “qué tan fuerte reacciona la instancia ante un cambio del modelo parámetros”multiplicados por" cuánto cambian los parámetros cuando aumentamos el peso de la instancia z". Otra forma de leer la fórmula: La influencia es proporcional a cuán grandes son los gradientes para el entrenamiento y la pérdida de pruebas. Cuanto mayor es el gradiente de la pérdida de entrenamiento, mayor es su influencia en los parámetros y mayor es la influencia en la predicción de la prueba. Cuanto mayor sea el gradiente de la predicción de prueba, más influyente será la instancia de prueba. Toda la construcción también se puede ver como una medida de la similitud (según lo aprendido por el modelo) entre el entrenamiento y la instancia de prueba.

Eso es todo con teoría e intuición. La siguiente sección explica cómo se pueden aplicar las funciones de influencia.

Aplicación de funciones de influencia

Las funciones de influencia tienen muchas aplicaciones, algunas de las cuales ya se han presentado en este capítulo.

Comprender el comportamiento del modelo

Diferentes modelos de aprendizaje automático tienen diferentes formas de hacer predicciones. Incluso si dos modelos tienen el mismo rendimiento, la forma en que hacen predicciones a partir de las características puede ser muy diferente y, por lo tanto, fallar en diferentes escenarios. Comprender las debilidades particulares de un modelo mediante la identificación de instancias influyentes ayuda a formar un “modelo mental” del comportamiento del modelo de aprendizaje automático en su mente. La siguiente figura muestra un ejemplo en el que se entrenó una SVM y una red neuronal para distinguir imágenes de perros y peces. Las instancias más influyentes de una imagen de un pez fueron muy diferentes para ambos modelos. Para el SVM, las instancias fueron influyentes si eran similares en color. Para la red neuronal, las instancias eran influyentes si eran conceptualmente similares. Para la red neuronal, incluso una imagen de un perro se encontraba entre las imágenes más influyentes, lo que demuestra que aprendió los conceptos y no la distancia euclidiana en el espacio de color.

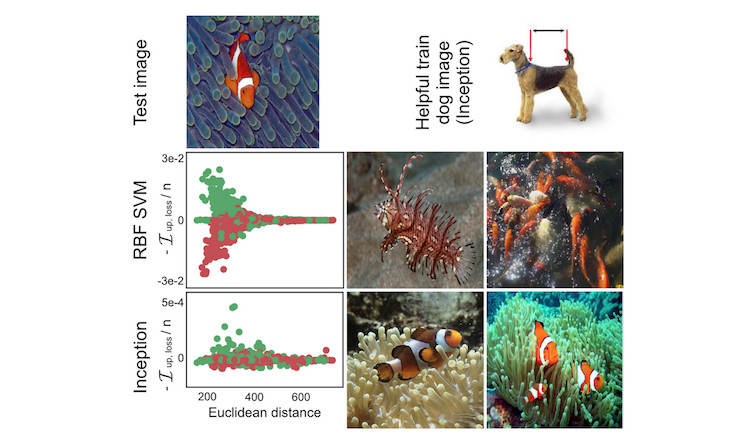
FIGURA 6.20: Perro o pez? Para la predicción SVM (fila central), las imágenes que tenían colores similares a la imagen de prueba fueron las más influyentes. Para la predicción de la red neuronal (fila inferior), los peces en diferentes entornos fueron los más influyentes, pero también una imagen de perro (arriba a la derecha). Trabajo de Koh y Liang (2017).

Manejo de desajustes de dominio / Errores de modelo de depuración

El manejo de la falta de coincidencia de dominio está estrechamente relacionado para comprender mejor el comportamiento del modelo. La falta de coincidencia de dominio significa que la distribución de los datos de entrenamiento y prueba es diferente, lo que puede hacer que el modelo tenga un bajo rendimiento en los datos de prueba. Las funciones de influencia pueden identificar instancias de entrenamiento que causaron el error. Supón que has entrenado un modelo de predicción para el resultado de pacientes que se han sometido a cirugía. Todos estos pacientes provienen del mismo hospital. Ahora usas el modelo en otro hospital y observas que no funciona bien para muchos pacientes. Por supuesto, asumes que los dos hospitales tienen pacientes diferentes, y si observas tus datos, puedes ver que difieren en muchas características. ¿Pero cuáles son las características o instancias que han “roto” el modelo? Aquí también, las instancias influyentes son una buena manera de responder esta pregunta. Tomas uno de los nuevos pacientes, para quienes el modelo ha hecho una predicción falsa, encuentra y analiza las instancias más influyentes. Por ejemplo, esto podría mostrar que el segundo hospital tiene pacientes mayores en promedio y las instancias más influyentes de los datos de entrenamiento son los pocos pacientes mayores del primer hospital y el modelo simplemente carecía de los datos para aprender a predecir bien este subgrupo. La conclusión sería que el modelo debe entrenarse en más pacientes mayores para que funcionen bien en el segundo hospital.

Fijación de datos de entrenamiento

Si tienes un límite en la cantidad de instancias de entrenamiento que puede verificar para verificar que sean correctas, ¿cómo haces una selección eficiente? La mejor manera es seleccionar las instancias más influyentes, porque, por definición, tienen la mayor influencia en el modelo. Incluso si tuvieras una instancia con valores obviamente incorrectos, si la instancia no es influyente y solo necesitas los datos para el modelo de predicción, es una mejor opción verificar las instancias influyentes. Por ejemplo, entrenas un modelo para predecir si un paciente debe permanecer en el hospital o ser dado de alta temprano. Realmente deseas asegurarte de que el modelo sea robusto y haga predicciones correctas, porque una liberación incorrecta de un paciente puede tener malas consecuencias. Los registros de pacientes pueden ser muy desordenados, por lo que no tienes una confianza perfecta en la calidad de los datos. Pero verificar la información del paciente y corregirla puede llevar mucho tiempo, porque una vez que ha informado qué pacientes debe verificar, el hospital realmente necesita enviar a alguien para que revise los registros de los pacientes seleccionados más de cerca, lo que podría estar escrito a mano y acostado en algún archivo. Verificar los datos de un paciente puede llevar una hora o más. En vista de estos costos, tiene sentido verificar solo algunas instancias de datos importantes. La mejor manera es seleccionar pacientes que hayan tenido una gran influencia en el modelo de predicción. Koh y Liang (2017) mostraron que este tipo de selección funciona mucho mejor que la selección aleatoria o la selección de aquellos con la mayor pérdida o clasificación incorrecta.

6.4.3 Ventajas de identificar instancias influyentes

Los enfoques de diagnóstico de eliminación y las funciones de influencia son muy diferentes de los enfoques basados principalmente en perturbaciones de características presentados en el Capítulo Modelos agnósticos. Una mirada a instancias influyentes enfatiza el papel de los datos de entrenamiento en el proceso de aprendizaje. Esto hace que las funciones de influencia y los diagnósticos de eliminación sean una de las mejores herramientas de depuración para los modelos de aprendizaje automático. De las técnicas presentadas en este libro, son las únicas que ayudan directamente a identificar las instancias que deben verificarse en busca de errores.

Los diagnósticos de eliminación son independientes del modelo, lo que significa que el enfoque se puede aplicar a cualquier modelo. También las funciones de influencia basadas en los derivados se pueden aplicar a una amplia clase de modelos.

Podemos usar estos métodos para comparar diferentes modelos de aprendizaje automático y comprender mejor sus diferentes comportamientos, yendo más allá de comparar solo el rendimiento predictivo.

No hemos hablado sobre este tema en este capítulo, pero las funciones de influencia a través de derivados también se pueden usar para crear datos de entrenamiento adversos. Estas son instancias que se manipulan de tal manera que el modelo no puede predecir ciertas instancias de prueba correctamente cuando el modelo está entrenado en esas instancias manipuladas. La diferencia con los métodos en el Capítulo de ejemplos adversos es que el ataque tiene lugar durante el tiempo de entrenamiento, también conocido como ataques de envenenamiento. Si estás interesado, lee el artículo de Koh y Liang (2017).

Para el diagnóstico de eliminación y las funciones de influencia, consideramos la diferencia en la predicción y para la función de influencia el aumento de la pérdida. Pero, realmente, el enfoque es generalizable a cualquier pregunta de la forma: “¿Qué le sucede a … cuando borramos o aumentamos la instancia z?”, Donde puedes llenar “…” con cualquier función de su modelo de su deseo. Puedes analizar cuánto influye una instancia de entrenamiento en la pérdida general del modelo. Puedes analizar cuánto influye una instancia de entrenamiento en la importancia de la función. Puedes analizar cuánto influye una instancia de entrenamiento en qué característica se selecciona para la primera división al entrenar un árbol de decisión.

6.4.4 Desventajas de identificar instancias influyentes

Los diagnósticos de eliminación son muy costosos de calcular porque requieren un nuevo entrenamiento. Pero la historia ha demostrado que los recursos informáticos aumentan constantemente. Un cálculo que hace 20 años era impensable en términos de recursos se puede realizar fácilmente con su teléfono inteligente. Puedes entrenar modelos con miles de instancias de entrenamiento y cientos de parámetros en una computadora portátil en segundos / minutos. Por lo tanto, no es un gran salto suponer que los diagnósticos de eliminación funcionarán sin problemas incluso con grandes redes neuronales en 10 años.

Las funciones de influencia son una buena alternativa al diagnóstico de eliminación, pero solo para modelos con parámetros diferenciables, como las redes neuronales. No funcionan para métodos basados en árboles como bosques aleatorios, árboles potenciados o árboles de decisión. Incluso si tienes modelos con parámetros y una función de pérdida, la pérdida puede no ser diferenciable. Pero para el último problema, hay un truco: Usa una pérdida diferenciable como sustituto para calcular la influencia cuando, por ejemplo, el modelo subyacente usa la función de pérdida Hinge Loss en lugar de alguna pérdida diferenciable. La pérdida se reemplaza por una versión suavizada de la pérdida problemática para las funciones de influencia, pero el modelo aún se puede entrenar con la pérdida no uniforme.

Las funciones de influencia son solo aproximadas, porque el enfoque forma una expansión cuadrática alrededor de los parámetros. La aproximación puede ser incorrecta y la influencia de una instancia en realidad es mayor o menor cuando se elimina. Koh y Liang (2017) mostraron para algunos ejemplos que la influencia calculada por la función de influencia estaba cerca de la medida de influencia obtenida cuando el modelo fue realmente reentrenado después de que se eliminó la instancia. Pero no hay garantía de que la aproximación siempre sea tan cercana.

No hay límite claro de la medida de influencia en la que llamamos una instancia influyente o no influyente. Es útil ordenar las instancias por influencia, pero sería genial tener los medios no solo para ordenar las instancias, sino para distinguir entre influyentes y no influyentes. Por ejemplo, si identificas las 10 instancias de entrenamiento más influyentes para una instancia de prueba, algunas de ellas pueden no ser influyentes porque, por ejemplo, solo las 3 principales fueron realmente influyentes.

Las medidas de influencia solo tienen en cuenta la eliminación de instancias individuales y no la eliminación de varias instancias a la vez. Grupos más grandes de instancias de datos pueden tener algunas interacciones que influyen fuertemente en el entrenamiento y predicción del modelo. Pero el problema radica en la combinatoria: Hay n posibilidades de eliminar una instancia individual de los datos. Hay n veces (n-1) posibilidades de eliminar dos instancias de los datos de entrenamiento. Hay n veces (n-1) veces (n-2) posibilidades de eliminar tres … Creo que puedes ver a dónde va esto, hay demasiadas combinaciones.

6.4.5 Software y alternativas

Los diagnósticos de eliminación son muy simples de implementar. Eche un vistazo al código que escribí para los ejemplos en este capítulo.

Para modelos lineales y modelos lineales generalizados, muchas medidas de influencia como la distancia de Cook se implementan en R en el paquete stats.

Koh y Liang publicaron el código de Python para funciones de influencia de su artículo en un repositorio. Eso es genial! Desafortunadamente, es “solo” el código del documento y no un módulo Python mantenido y documentado. El código se centra en la biblioteca Tensorflow, por lo que no puedes usarlo directamente para modelos de caja negra que usan otros marcos, como sci-kit learn.

Keita Kurita escribió una gran publicación de blog para funciones de influencia eso me ayudó a entender mejor el papel de Koh y Liang. La publicación del blog profundiza un poco más en las matemáticas detrás de las funciones de influencia para los modelos de caja negra y también habla sobre algunos de los ‘trucos’ matemáticos con los que el método se implementa de manera eficiente.

---

58. Cook, R. Dennis. “Detection of influential observation in linear regression.” Technometrics 19.1 (1977): 15-18.↩

59. Koh, Pang Wei, and Percy Liang. “Understanding black-box predictions via influence functions.” arXiv preprint arXiv:1703.04730 (2017).↩