4.3 GLM, GAM y más

La mayor fortaleza, pero también la mayor debilidad del modelo de regresión lineal es que la predicción se modela como una suma ponderada de las características. Además, el modelo lineal trae muchos otros supuestos. La mala noticia (bueno, en realidad no es noticia) es que todos esos supuestos a menudo se violan en la realidad: El objetivo condicionado a las características podría tener una distribución no gaussiana, las características podrían interactuar y la relación entre las características y el resultado podría no ser lineal. La buena noticia es que la comunidad de estadísticos ha desarrollado una variedad de modificaciones que transforman el modelo de regresión lineal de una hoja simple a una navaja suiza.

Este capítulo no es tu guía definitiva para extender modelos lineales. Por el contrario, sirve como una descripción general de las extensiones como los Modelos lineales generalizados (GLM) y los Modelos aditivos generalizados (GAM), y da una pequeña intuición. Después de leer, debes tener una descripción general sólida de cómo extender modelos lineales. Si deseas obtener más información sobre el modelo de regresión lineal primero, te sugiero que leas el capítulo sobre modelos de regresión lineal, si aún no lo has hecho.

Recordemos la fórmula de un modelo de regresión lineal:

\[y=\beta_{0}+\beta_{1}x_{1}+\ldots+\beta_{p}x_{p}+\epsilon\]

El modelo de regresión lineal supone que el resultado Y de una instancia puede expresarse mediante una suma ponderada de sus características p con un error individual \(\epsilon\) que sigue una distribución gaussiana. Al forzar los datos en este corset de una fórmula, obtenemos mucha interpretación del modelo. Los efectos de las características son aditivos, lo que significa que no hay interacciones, y la relación es lineal, lo que significa que un aumento de una característica en una unidad debe traducirse directamente en un aumento / disminución del resultado previsto. El modelo lineal nos permite comprimir la relación entre una característica y el resultado esperado en un solo número, es decir, el peso estimado.

Pero una suma ponderada simple es demasiado restrictiva para muchos problemas de predicción del mundo real. En este capítulo aprenderemos sobre tres problemas del modelo clásico de regresión lineal y cómo resolverlos. Hay muchos más problemas con supuestos posiblemente violados, pero nos centraremos en los tres que se muestran en la siguiente figura:

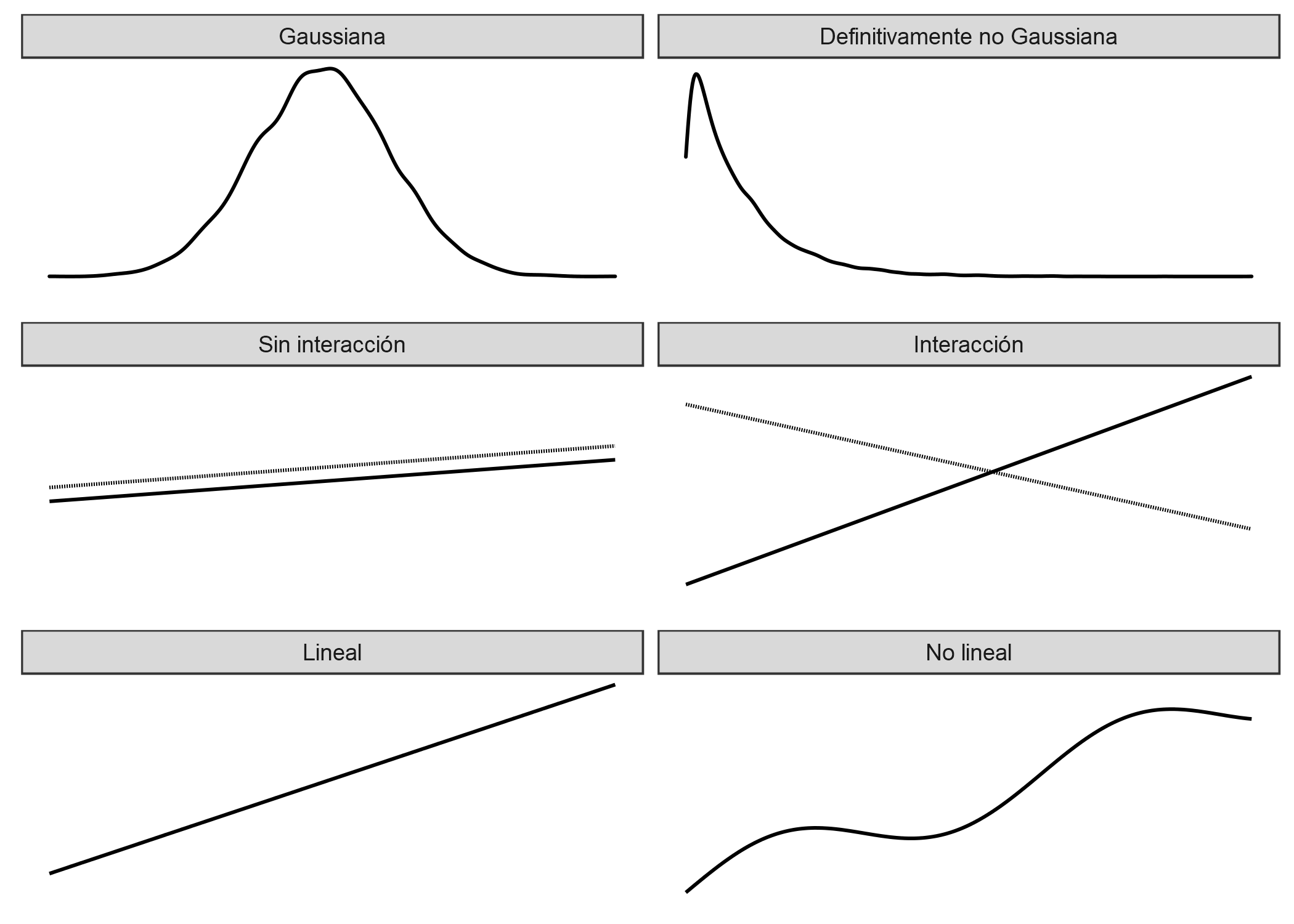
FIGURA 4.8: Tres supuestos del modelo lineal (lado izquierdo): distribución gaussiana del resultado dadas las características, la aditividad (= sin interacciones) y la relación lineal. La realidad generalmente no se adhiere a esos supuestos (lado derecho): los resultados pueden tener distribuciones no gaussianas, las características pueden interactuar y la relación puede ser no lineal.

Hay una solución para todos estos problemas:

Problema: El resultado objetivo y dadas las características no sigue una distribución gaussiana. Ejemplo: supongamos que quiero predecir cuántos minutos voy a andar en bicicleta en un día determinado. Como características tengo el tipo de día, el clima, etc. Si uso un modelo lineal, podría predecir minutos negativos porque supone una distribución gaussiana que no se detiene en 0 minutos. Además, si quiero predecir probabilidades con un modelo lineal, puedo obtener probabilidades que son negativas o mayores que 1. Solución: Modelos lineales generalizados (GLM).

Problema: las características interactúan. Ejemplo: En promedio, la lluvia ligera tiene un ligero efecto negativo en mi deseo de ir en bicicleta. Pero en verano, durante las horas pico, doy la bienvenida a la lluvia, ¡porque entonces todos los ciclistas de buen tiempo se quedan en casa y tengo los carriles bici para mí! Esta es una interacción entre el tiempo y el clima que no puede ser capturada por un modelo puramente aditivo. Solución: Agregar interacciones manualmente.

Problema: La verdadera relación entre las características e Y no es lineal. Ejemplo: Entre 0 y 25 grados Celsius, la influencia de la temperatura en mi deseo de andar en bicicleta podría ser lineal, lo que significa que un aumento de 0 a 1 grado causa el mismo aumento en el deseo de ciclismo que un aumento de 20 a 21. Pero a temperaturas más altas, mi motivación para completar el ciclo se nivela e incluso disminuye: no me gusta andar en bicicleta cuando hace demasiado calor. Soluciones: Modelos aditivos generalizados (GAM); transformación de características.

Las soluciones a estos tres problemas se presentan en este capítulo. Se omiten muchas extensiones adicionales del modelo lineal. Si intentara cubrir todo aquí, el capítulo se convertiría rápidamente en un libro dentro de un libro, sobre un tema que ya está cubierto en muchos otros libros. Pero como ya estás aquí, he hecho un pequeño problema+solución para las extensiones de modelo lineal, que puedes encontrar al final del capítulo. El nombre de la solución está destinado a servir como punto de partida para una búsqueda.

4.3.1 Resultados no gaussianos: GLM

El modelo de regresión lineal supone que el resultado, dadas las características de entrada, sigue una distribución gaussiana. Este supuesto excluye muchos casos: El resultado también puede ser una categoría (cáncer versus salud), un recuento (número de niños), el tiempo hasta la ocurrencia de un evento (tiempo hasta el fallo de una máquina) o un resultado muy sesgado con unos valores muy altos (como el ingreso familiar). El modelo de regresión lineal se puede extender para modelar todos estos tipos de resultados. Esta extensión se llama Modelos lineales generalizados o GLM para abreviar. A lo largo de este capítulo, usaré el nombre GLM tanto para el marco general como para modelos particulares de ese marco. El concepto central de cualquier GLM es: Mantener la suma ponderada de las características, pero permitiendo distribuciones de resultados no gaussianas, y conectando la media esperada de esta distribución y la suma ponderada a través de una función posiblemente no lineal. Por ejemplo, el modelo de regresión logística supone una distribución de Bernoulli para el resultado y vincula la media esperada y la suma ponderada utilizando la función logística.

El GLM vincula matemáticamente la suma ponderada de las características con el valor medio de la distribución asumida utilizando la función de enlace g, que se puede elegir de manera flexible dependiendo del tipo de resultado.

\[g(E_Y(y|x))=\beta_0+\beta_1{}x_{1}+\ldots{}\beta_p{}x_{p}\]

Los GLM consisten en tres componentes: La función de enlace g, la suma ponderada \(X^T\beta\) (a veces llamada predictor lineal) y una distribución de probabilidad de la familia exponencial que define \(E_Y\).

La familia exponencial es un conjunto de distribuciones que se pueden escribir con la misma fórmula (parametrizada) que incluye un exponente, la media y varianza de la distribución y algunos otros parámetros. No entraré en los detalles matemáticos porque este es un universo muy grande. Wikipedia tiene una lista de distribuciones ordenada de la familia exponencial. Puedes elegir cualquier distribución de esta lista para tu GLM. Según el tipo de resultado que deseas predecir, elige una distribución adecuada. ¿El resultado es un conteo de algo (por ejemplo, número de niños que viven en un hogar)? Entonces la distribución de Poisson podría ser una buena opción. ¿El resultado es siempre positivo (por ejemplo, tiempo entre dos eventos)? Entonces la distribución exponencial podría ser una buena opción.

Consideremos el modelo lineal clásico como un caso especial de un GLM. La función de enlace para la distribución gaussiana en el modelo lineal clásico es simplemente la función de identidad. La distribución gaussiana se parametriza por la media y los parámetros de varianza. La media describe el valor que esperamos en promedio y la varianza describe cuánto varían los valores en torno a esta media. En el modelo lineal, la función de enlace vincula la suma ponderada de las características con la media de la distribución gaussiana.

Bajo el marco GLM, este concepto se generaliza a cualquier distribución (de la familia exponencial), con funciones de enlace arbitrarias. Si Y es un conteo de algo, como la cantidad de cafés que alguien bebe en un día determinado, podríamos modelarlo con un GLM con una distribución de Poisson y el logaritmo natural como función de enlace:

\[ln(E_Y(y|x))=x^{T}\beta\]

El modelo de regresión logística también es un GLM que asume una distribución de Bernoulli y utiliza la función logit como función de enlace. La media de la distribución binomial utilizada en la regresión logística es la probabilidad de que Y sea 1.

\[x^{T}\beta=ln\left(\frac{E_Y(y|x)}{1-E_Y(y|x)}\right)=ln\left(\frac{P(y=1|x)}{1-P(y=1|x)}\right)\]

Y si resolvemos esta ecuación para tener P(y=1) en un lado, obtenemos la fórmula de regresión logística:

\[P(y=1)=\frac{1}{1+exp(-x^{T}\beta)}\]

Cada distribución de la familia exponencial tiene una función de enlace canónica, que puede derivarse matemáticamente de la distribución. El marco GLM permite elegir la función de enlace independientemente de la distribución. ¿Cómo elegir la función de enlace correcta? No hay una receta perfecta. Hay que tener en cuenta el conocimiento sobre la distribución del objetivo, pero también las consideraciones teóricas y qué tan bien el modelo se ajusta a tus datos reales. Para algunas distribuciones, la función de enlace canónica puede conducir a valores que no son válidos para esa distribución. En el caso de la distribución exponencial, la función de enlace canónica es el inverso negativo, que puede conducir a predicciones negativas que están fuera del dominio de la distribución exponencial. Como puedes elegir cualquier función de enlace, la solución simple es elegir otra función que respete el dominio de la distribución.

Ejemplos

He simulado un conjunto de datos sobre el comportamiento del consumo de café para resaltar la necesidad de GLM. Supongamos que has recopilado datos sobre tu comportamiento diario de consumo de café. Si no te gusta el café, finge que se trata de té. Junto con la cantidad de tazas, registras tu nivel de estrés actual en una escala del 1 al 10, qué tan bien dormías la noche anterior en una escala del 1 al 10 y si tuviste que trabajar ese día. El objetivo es predecir la cantidad de cafés, dadas las características de estrés, sueño y trabajo. Simulé datos durante 200 días. El estrés y el sueño se dibujaron uniformemente entre 1 y 10 y el trabajo sí/no se dibujó con una probabilidad de 50/50 (¡qué vida!). Para cada día, el número de cafés se extrajo de una distribución de Poisson, modelando la intensidad \(\lambda\) (que también es el valor esperado de la distribución de Poisson) en función de las características sueño, estrés y trabajo. Puedes adivinar a dónde llevará esta historia: “Oye, modelemos estos datos con un modelo lineal … Oh, no funciona … Probemos un GLM con distribución de Poisson … ¡SORPRESA! ¡Ahora funciona!”. Espero no haberte arruinado demasiado la historia.

Veamos la distribución de la variable objetivo, la cantidad de cafés en un día determinado:

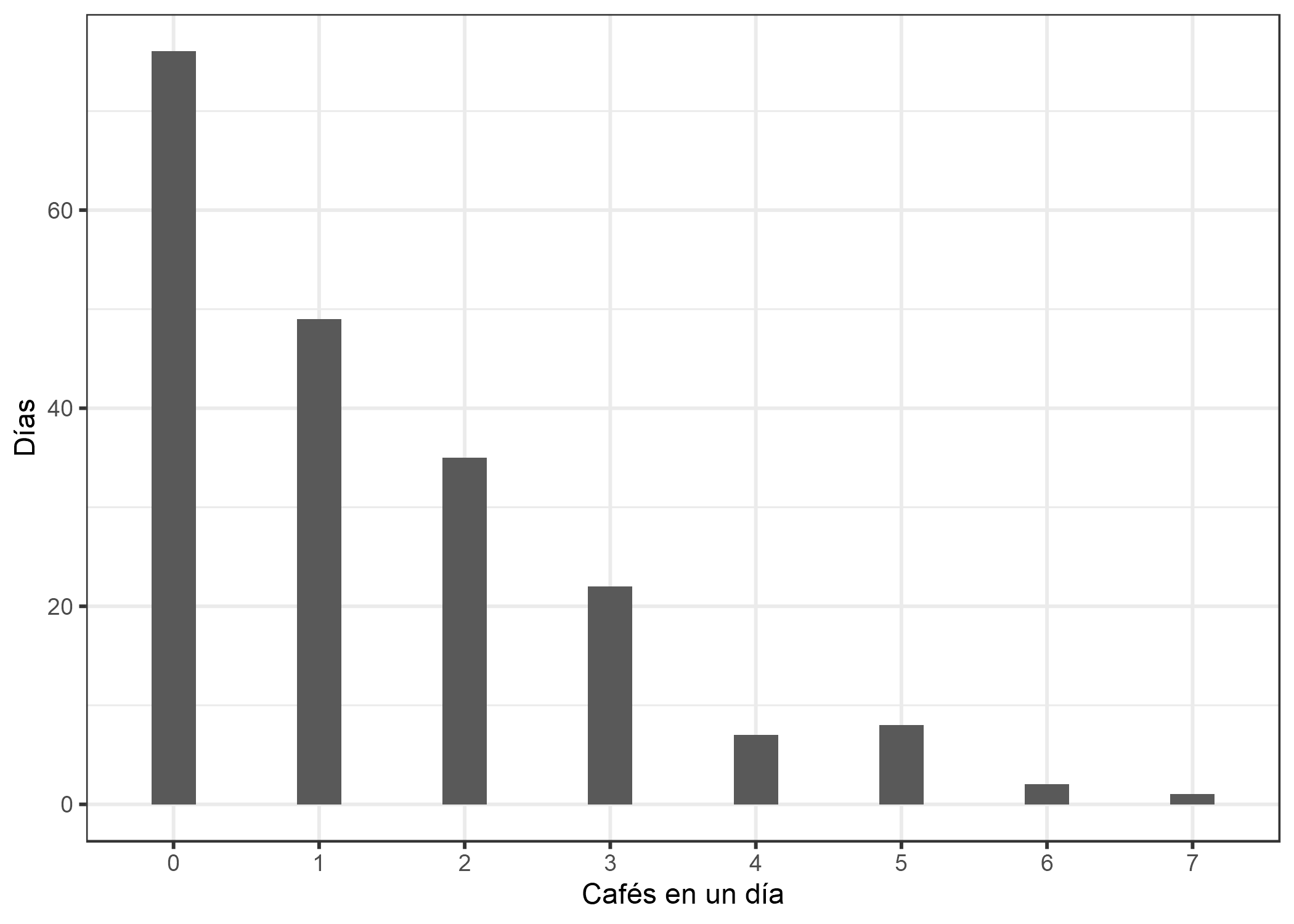
FIGURA 4.9: Distribución simulada del número de cafés diarios durante 200 días.

En 76 de los días 200 no tomaste café y en el día más extremo tomaste 7. Usemos ingenuamente un modelo lineal para predecir la cantidad de cafés usando el nivel de sueño, el nivel de estrés y el trabajo sí/no como características. ¿Qué puede salir mal cuando asumimos falsamente una distribución gaussiana? Un supuesto erróneo puede invalidar las estimaciones, especialmente los intervalos de confianza de los pesos. Un problema más obvio es que las predicciones no coinciden con el dominio “permitido” del resultado real, como muestra la siguiente figura.

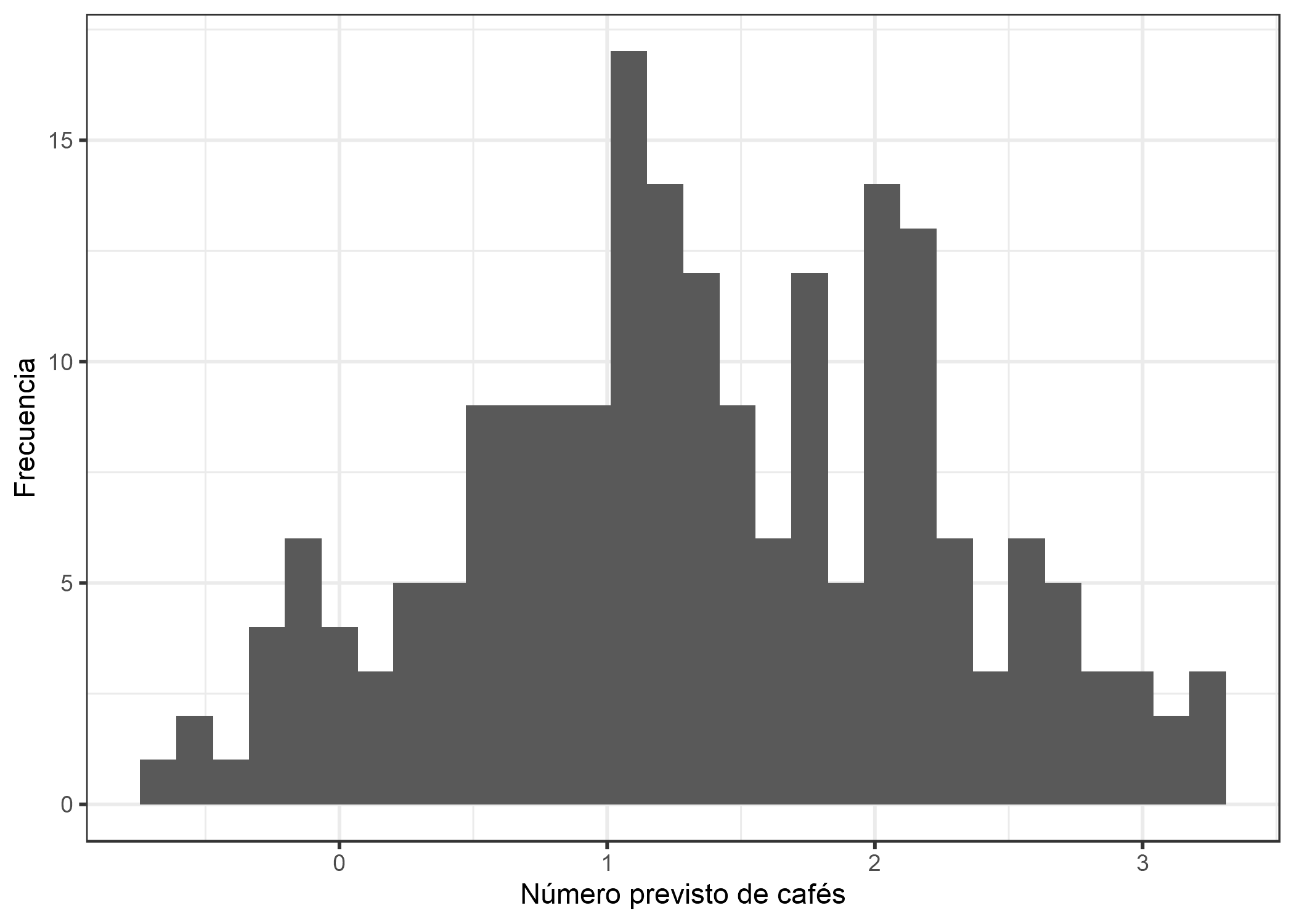
FIGURA 4.10: Número previsto de cafés dependientes del estrés, el sueño y el trabajo. El modelo lineal predice valores negativos.

El modelo lineal no tiene sentido, porque predice un número negativo de cafés. Este problema se puede resolver con los modelos lineales generalizados (GLM). Podemos cambiar la función de enlace y la distribución asumida. Una posibilidad es mantener la distribución gaussiana y usar una función de enlace que siempre conduzca a predicciones positivas como el log-link (inversa de la función exp) en lugar de la función de identidad. Aun mejor: Elegimos una distribución que corresponde al proceso de generación de datos y una función de enlace apropiada. Como el resultado es un recuento, la distribución de Poisson es una elección natural, junto con el logaritmo como función de enlace. En este caso, los datos incluso se generaron con la distribución de Poisson, por lo que Poisson GLM es la elección perfecta. El Poisson GLM ajustado conduce a la siguiente distribución de valores pronosticados:

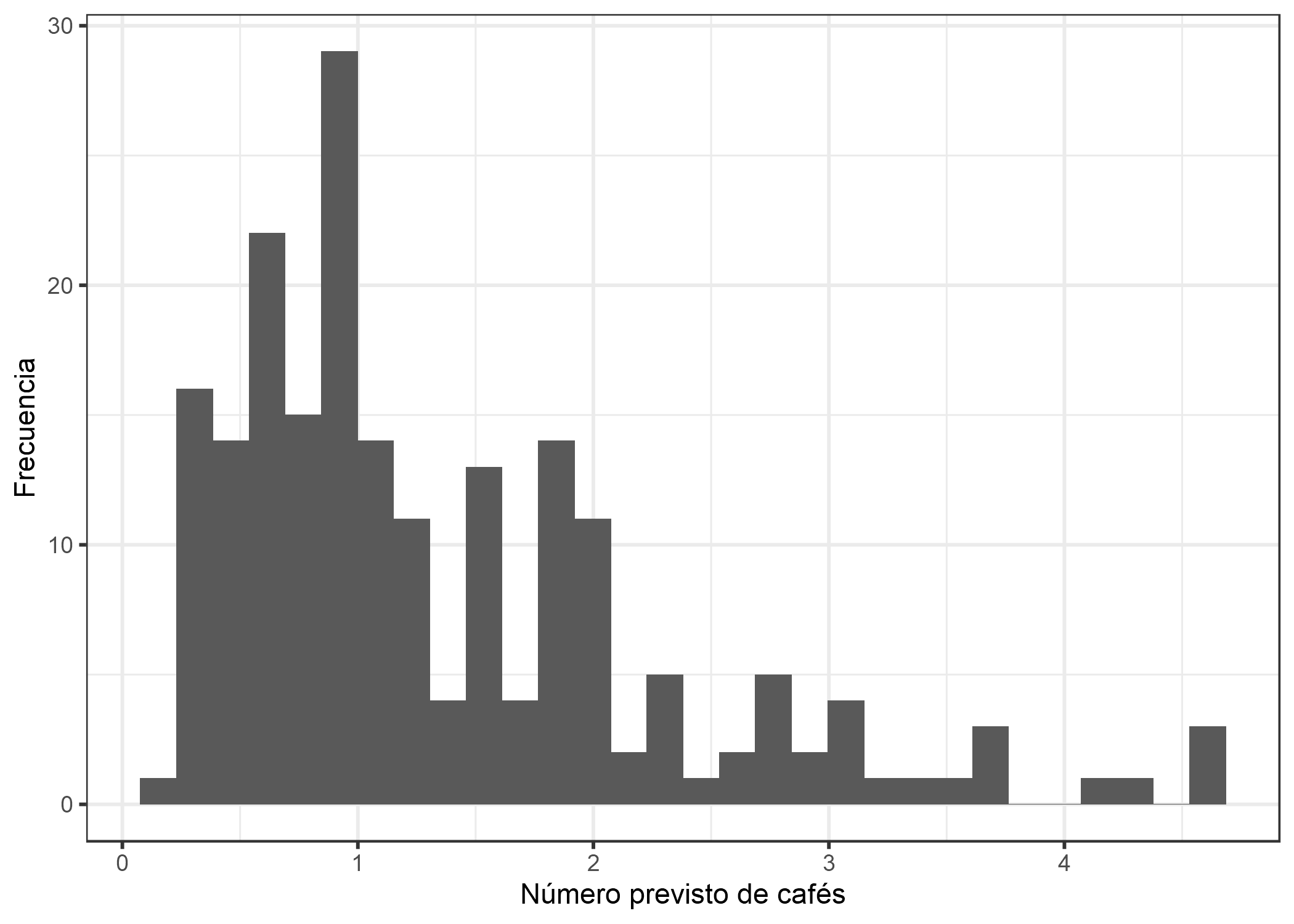
FIGURA 4.11: Número previsto de cafés que dependen del estrés, el sueño y el trabajo. El GLM con el supuesto de Poisson y el log-link es un modelo apropiado para este conjunto de datos.

No hay cantidades negativas de cafés, se ve mucho mejor ahora.

Interpretación de los pesos GLM

La distribución asumida junto con la función de enlace determina cómo se interpretan los pesos estimados de las características. En el ejemplo del recuento de café, utilicé un GLM con distribución de Poisson y enlace de registro, lo que implica la siguiente relación entre las características y el resultado esperado.

\[ln(E(\text{coffees}|\text{stress},\text{sleep},\text{workYES}))=\beta_0+\beta_{\text{stress}}x_{\text{stress}}+\beta_{\text{sleep}}x_{\text{sleep}}+\beta_{\text{workYES}}x_{\text{workYES}}\]

Para interpretar los pesos, invertimos la función de enlace para poder interpretar el efecto de las características en el resultado esperado y no en el logaritmo del resultado esperado.

\[E(\text{coffees}|\text{stress},\text{sleep},\text{workYES})=exp(\beta_0+\beta_{\text{stress}}x_{\text{stress}}+\beta_{\text{sleep}}x_{\text{sleep}}+\beta_{\text{workYES}}x_{\text{workYES}})\]

Como todos los pesos están en la función exponencial, la interpretación del efecto no es aditiva, sino multiplicativa, porque exp(a + b) es exp (a) por exp (b). El último ingrediente para la interpretación son los pesos reales del ejemplo del juguete. La siguiente tabla enumera los pesos estimados y exp(pesos) junto con el intervalo de confianza del 95%:

	peso	exp(peso) [2.5%, 97.5%]
(Intercept)	-0.16	0.85 [0.54, 1.32]
stress	0.12	1.12 [1.07, 1.18]
sleep	-0.15	0.86 [0.82, 0.90]
workYES	0.80	2.23 [1.72, 2.93]

Aumentar el nivel de estrés en un punto multiplica el número esperado de cafés por el factor 1.12. Aumentar la calidad del sueño en un punto multiplica el número esperado de cafés por el factor 0.86. El número previsto de cafés en un día de trabajo es en promedio 2.23 veces el número de cafés en un día libre. En resumen, cuanto más estrés, menos sueño y más trabajo, más café se consume.

En esta sección, aprendiste un poco sobre los modelos lineales generalizados que son útiles cuando el objetivo no sigue una distribución gaussiana. A continuación, veremos cómo integrar las interacciones entre dos características en el modelo de regresión lineal.

4.3.2 Interacciones

El modelo de regresión lineal supone que el efecto de una característica es el mismo independientemente de los valores de las otras características (= sin interacciones). Pero a menudo hay interacciones en los datos. Para predecir el número de bicicletas alquilados, puede haber una interacción entre la temperatura y si es un día hábil o no. Quizás, cuando las personas tienen que trabajar, la temperatura no influye mucho en el número de bicicletas alquiladas, porque las personas andarán en la bicicleta alquilada para trabajar, pase lo que pase. En los días libres, muchas personas viajan por placer, pero solo cuando hace suficiente calor. Cuando se trata de alquilar bicicletas, se puede esperar una interacción entre la temperatura y la jornada laboral.

¿Cómo podemos lograr que el modelo lineal incluya interacciones? Antes de ajustar el modelo lineal, agrega una columna a la matriz de características que represente la interacción entre las características y ajuste el modelo como de costumbre. La solución es elegante en cierto modo, ya que no requiere ningún cambio del modelo lineal, solo columnas adicionales en los datos. En el ejemplo de la jornada laboral y la temperatura, agregaríamos una nueva característica que tiene ceros para los días sin trabajo, de lo contrario tiene el valor de la característica de temperatura, suponiendo que la jornada laboral sea la categoría de referencia. Supongamos que nuestros datos se ven así:

trabajo	temp
Y	25
N	12
N	30
Y	5

La matriz de datos utilizada por el modelo lineal se ve ligeramente diferente. La siguiente tabla muestra el aspecto de los datos preparados para el modelo si no especificamos ninguna interacción. Normalmente, esta transformación se realiza automáticamente por cualquier software estadístico.

Intercepto	trabajoY	temp
1	1	25
1	0	12
1	0	30
1	1	5

La primera columna es el intercepto. La segunda columna codifica la característica categórica, con 0 para la categoría de referencia y 1 para la otra. La tercera columna contiene la temperatura.

Si queremos que el modelo lineal considere la interacción entre la temperatura y la característica de día laborable, debemos agregar una columna para la interacción:

Intercepto	trabajoY	temp	trabajoY.temp
1	1	25	25
1	0	12	0
1	0	30	0
1	1	5	5

La nueva columna “workY.temp” captura la interacción entre las características día laborable (trabajo) y temperatura (temperatura). Esta nueva columna de características es cero para una instancia si la característica de trabajo está en la categoría de referencia (“N”), de lo contrario, asume los valores de la característica de temperatura de instancias. Con este tipo de codificación, el modelo lineal puede aprender un efecto lineal diferente de la temperatura para ambos tipos de días. Este es el efecto de interacción entre las dos características. Sin un término de interacción, el efecto combinado de una característica categórica y numérica se puede describir mediante una línea que se desplaza verticalmente para las diferentes categorías. Si incluimos la interacción, permitimos que el efecto de las características numéricas (la pendiente) tenga un valor diferente en cada categoría.

La interacción de dos características categóricas funciona de manera similar. Creamos características adicionales que representan combinaciones de categorías. Aquí hay algunos datos artificiales que contienen el día laboral (trabajo) y una característica meteorológica categórica (wthr):

trabajo	wthr
Y	2
N	0
N	1
Y	2

A continuación, incluimos términos de interacción:

Intercepto	trabajoY	wthr1	wthr2	trabajoY.wthr1	trabajoY.wthr2
1	1	0	1	0	1
1	0	0	0	0	0
1	0	1	0	0	0
1	1	0	1	0	1

La primera columna sirve para estimar el intercepto. La segunda columna es la característica de trabajo codificada. Las columnas tres y cuatro son para la característica del clima, que requiere dos columnas porque necesita dos pesos para capturar el efecto para tres categorías, una de las cuales es la categoría de referencia. El resto de las columnas capturan las interacciones. Para cada categoría de ambas características (excepto las categorías de referencia), creamos una nueva columna de características que es 1 si ambas características tienen una determinada categoría, de lo contrario 0.

Para dos características numéricas, la columna de interacción es aún más fácil de construir: Simplemente multiplicamos ambas características numéricas.

Existen enfoques para detectar y agregar automáticamente términos de interacción. Uno de ellos se puede encontrar en el Capítulo de RuleFit. El algoritmo RuleFit primero mina los términos de interacción y luego estima un modelo de regresión lineal que incluye interacciones.

Nota del traductor: Para un ejemplo de términos de interacción consultar la versión original en inglés.

4.3.3 Efectos no lineales - GAM

El mundo no es lineal. La linealidad en los modelos lineales significa que no importa qué valor tenga una instancia en una característica particular, aumentar el valor en una unidad siempre tiene el mismo efecto en el resultado previsto. ¿Es razonable suponer que aumentar la temperatura en un grado a 10 grados centígrados tiene el mismo efecto en el número de bicicletas de alquiler que aumentar la temperatura cuando ya tiene 40 grados? Intuitivamente, uno espera que el aumento de la temperatura de 10 a 11 grados centígrados tenga un efecto positivo en el alquiler de bicicletas y de 40 a 41 un efecto negativo, que también es el caso, como verás, en muchos ejemplos a lo largo del libro. La característica de la temperatura tiene un efecto lineal y positivo en el número de bicicletas de alquiler, pero en algún momento se aplana e incluso tiene un efecto negativo a altas temperaturas. Al modelo lineal no le importa, obedientemente encontrará el mejor plano lineal (minimizando la distancia euclidiana).

Puede modelar relaciones no lineales utilizando una de las siguientes técnicas:

• Transformación simple de la característica (por ejemplo, logaritmo)
• Categorización de la función
• Modelos aditivos generalizados (GAM)

Antes de entrar en los detalles de cada método, comencemos con un ejemplo que ilustra los tres. Tomé el conjunto de datos de alquiler de bicicletas y entrené un modelo lineal con solo la función de temperatura para predecir el número de bicicletas de alquiler. La siguiente figura muestra la pendiente estimada con: el modelo lineal estándar, un modelo lineal con temperatura transformada (logaritmo), un modelo lineal con temperatura tratada como característica categórica y utilizando splines de regresión (GAM).

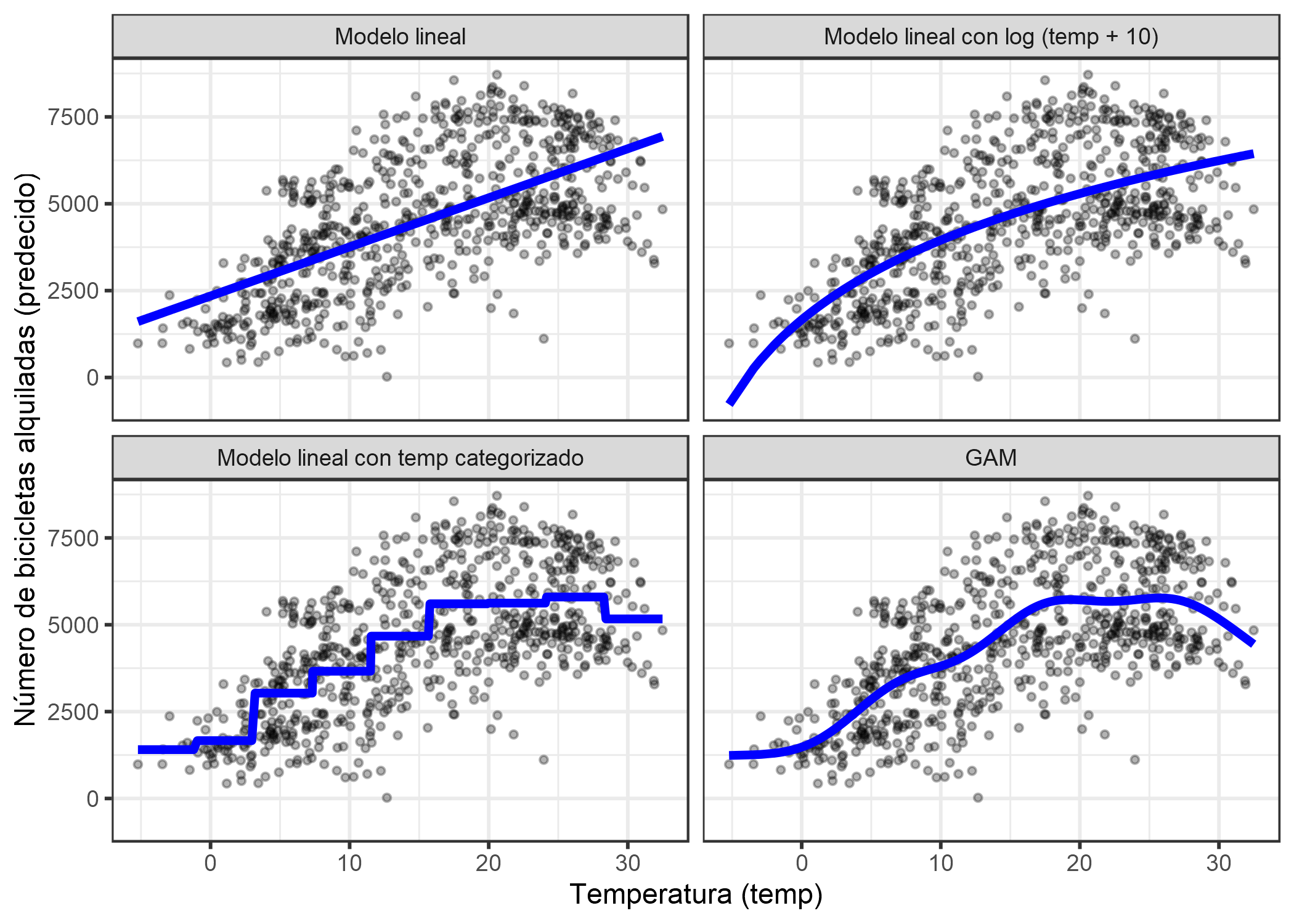
FIGURA 4.12: Predicción del número de bicicletas alquiladas utilizando solo la variable de temperatura. Un modelo lineal (arriba a la izquierda) no se ajusta bien a los datos. Una solución es transformar la función con, por ejemplo, logaritmo (arriba a la derecha), clasificarlo (abajo a la izquierda), que generalmente es una mala decisión, o usar modelos de aditivos generalizados que puedan ajustarse automáticamente a una curva suave de temperatura (abajo a la derecha).

Transformación de características

A menudo, el logaritmo de la característica se usa como una transformación. El uso del logaritmo indica que cada aumento de temperatura de 10 veces tiene el mismo efecto lineal en el número de bicicletas, por lo que cambiar de 1 grado Celsius a 10 grados Celsius tiene el mismo efecto que cambiando de 0.1 a 1 (suena mal). Otros ejemplos de transformaciones de características son la raíz cuadrada, la función cuadrada y la función exponencial. El uso de una transformación de característica significa que reemplaza la columna de esta característica en los datos con una función de la característica, como el logaritmo, y ajusta el modelo lineal como de costumbre. Algunos programas estadísticos también te permiten especificar transformaciones en la llamada del modelo lineal. Puedes ser creativo cuando transformas la función. La interpretación de la característica cambia según la transformación seleccionada. Si usas una transformación de logaritmo, la interpretación en un modelo lineal se convierte en: “Si el logaritmo de la característica aumenta en uno, la predicción aumenta en el peso correspondiente”. Cuando usas un GLM con una función de enlace que no es la función de identidad, la interpretación se vuelve más complicada, porque tienes que incorporar ambas transformaciones en la interpretación (excepto cuando se cancelan entre sí, como log y exp, donde la interpretación se hace más fácil).

Categorización de características

Otra posibilidad para lograr un efecto no lineal es discretizar la característica; conviértalo en una característica categórica. Por ejemplo, puede cortar la función de temperatura en 20 intervalos con los niveles [-10, -5), [-5, 0), … y así sucesivamente. Cuando utilizas la temperatura categorizada en lugar de la temperatura continua, el modelo lineal estimaría una función de paso porque cada nivel obtiene su propia estimación. El problema con este enfoque es que necesita más datos, es más probable que se sobreajuste y no está claro cómo discretizar la característica de manera significativa (intervalos equidistantes o cuantiles, ¿cuántos intervalos?). Solo usaría la discretización si hay un caso muy sólido para ello. Por ejemplo, para hacer que el modelo sea comparable a otro estudio.

Modelos aditivos generalizados (GAM)

¿Por qué no “simplemente” permitir que el modelo lineal (generalizado) aprenda relaciones no lineales? Esa es la motivación detrás de los GAM. Los GAM relajan la restricción de que la relación debe ser una simple suma ponderada y, en cambio, suponen que el resultado puede ser modelado por una suma de funciones arbitrarias de cada característica. Matemáticamente, la relación en un GAM se ve así:

\[g(E_Y(y|x))=\beta_0+f_1(x_{1})+f_2(x_{2})+\ldots+f_p(x_{p})\]

La fórmula es similar a la fórmula GLM con la diferencia de que el término lineal \(\beta_j{}x_{j}\) se reemplaza por una función más flexible \(f_j(x_{j})\). El núcleo de un GAM sigue siendo una suma de efectos de características, pero tiene la opción de permitir relaciones no lineales entre algunas características y la salida. Los efectos lineales también están cubiertos por el marco, porque para que las características se manejen linealmente, puede limitar sus \(f_j(x_{j})\) solo para tomar la forma de \(x_{j}\beta_j\).

La gran pregunta es cómo aprender funciones no lineales. La respuesta se llama “splines” o “funciones de spline”. Las splines son funciones que se pueden combinar para aproximar funciones arbitrarias. Un poco como apilar ladrillos de Lego para construir algo más complejo. Hay una cantidad confusa de formas de definir estas funciones de spline. Si estás interesado en aprender más sobre todas las formas de definir splines, te deseo buena suerte en tu viaje. No voy a entrar en detalles aquí, solo voy a construir una intuición. Lo que más me ayudó personalmente para comprender las splines fue visualizar las funciones individuales de splines y analizar cómo se modifica la matriz de datos. Por ejemplo, para modelar la temperatura con splines, eliminamos la característica de temperatura de los datos y la reemplazamos con, por ejemplo, 4 columnas, cada una de las cuales representa una función de spline. En general tendría más funciones de spline, solo reduje el número con fines ilustrativos. El valor para cada instancia de estas nuevas características de spline depende de los valores de temperatura de las instancias. Junto con todos los efectos lineales, el GAM también estima estos pesos spline. Los GAM también introducen un término de penalización para los pesos para mantenerlos cerca de cero. Esto reduce efectivamente la flexibilidad de las splines y reduce el sobreajuste. Un parámetro de suavidad que se usa comúnmente para controlar la flexibilidad de la curva se ajusta mediante validación cruzada. Ignorando el término de penalización, el modelado no lineal con splines es una ingeniería sofisticada.

En el ejemplo en el que estamos prediciendo el número de bicicletas con un GAM utilizando solo la temperatura, la siguiente figura muestra cómo se ven estas funciones de spline:

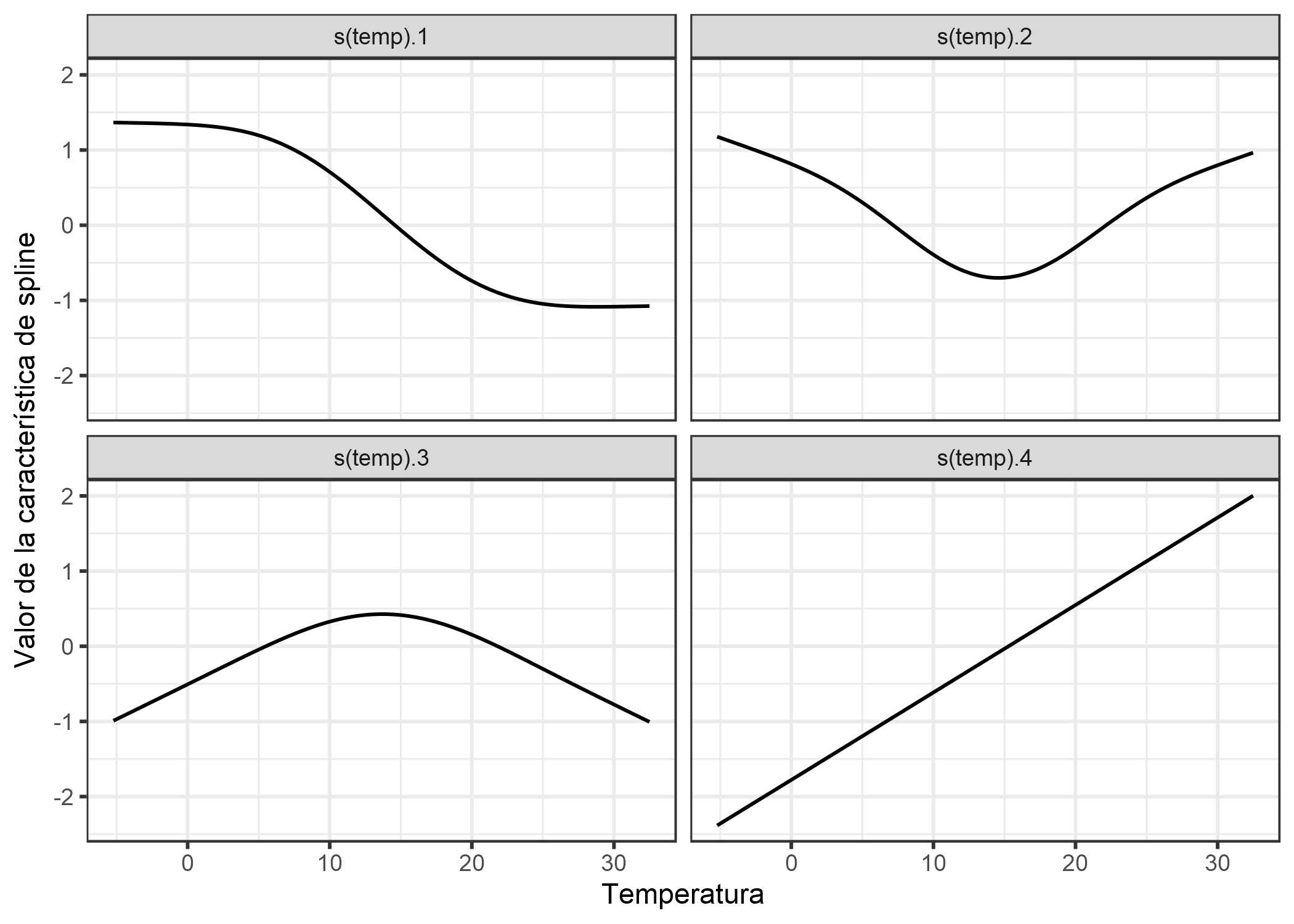
FIGURA 4.13: Para modelar suavemente el efecto de temperatura, utilizamos 4 funciones de spline. Cada valor de temperatura se asigna a (aquí) 4 valores de spline. Si una instancia tiene una temperatura de 30 ° C, la el valor para la primera característica de spline es -1, para el segundo 0.7, para el tercero -0.8 y para el cuarto 1.7.

La curva real, que resulta de la suma de las funciones de spline ponderadas con los pesos estimados, se ve así:

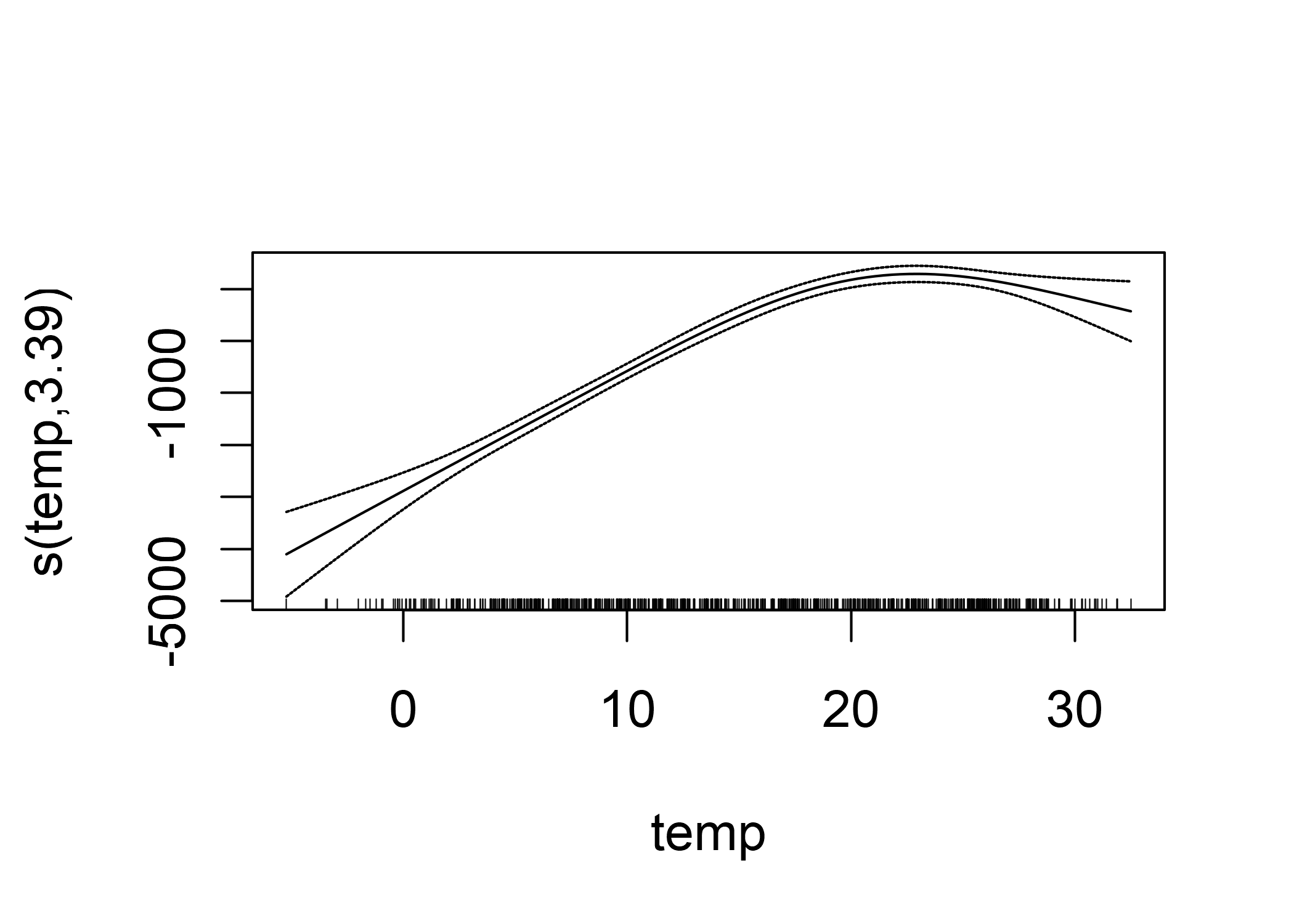
FIGURA 4.14: Efecto de la función GAM de la temperatura para predecir el número de bicicletas alquiladas (la temperatura se usa como la única característica).

La interpretación de los efectos suaves requiere una verificación visual de la curva ajustada. Las splines generalmente se centran alrededor de la predicción media, por lo que un punto en la curva es la diferencia con la predicción media. Por ejemplo, a 0 grados centígrados, el número previsto de bicicletas es 3000 menor que la predicción promedio.

4.3.4 Ventajas

Todas estas extensiones del modelo lineal son un poco un universo en sí mismas. Cualesquiera que sean los problemas que enfrentas con los modelos lineales, probablemente encontrarás una extensión que lo corrige.

La mayoría de los métodos se han utilizado durante décadas. Por ejemplo, los GAM tienen casi 30 años. Muchos investigadores y profesionales de la industria tienen mucha experiencia con modelos lineales y los métodos son aceptados en muchas comunidades como status quo para el modelado.

Además de hacer predicciones, puedes usar los modelos para hacer inferencia, sacar conclusiones sobre los datos, dado que los supuestos del modelo no se violan. Obtiene intervalos de confianza para pesos, pruebas de significación, intervalos de predicción y mucho más.

El software estadístico generalmente tiene interfaces realmente buenas para adaptarse a GLM, GAM y modelos lineales más especiales.

La opacidad de muchos modelos de aprendizaje automático proviene de 1) una falta de dispersión, lo que significa que se utilizan muchas características, 2) características que se tratan de manera no lineal, lo que significa que necesita más de un peso para describir el efecto, y 3) el modelado de interacciones entre las características. Suponiendo que los modelos lineales son altamente interpretables pero a menudo no se ajustan a la realidad, las extensiones descritas en este capítulo ofrecen una buena manera de lograr una transición suave hacia modelos más flexibles, al tiempo que conservan algo de la capacidad de interpretación.

4.3.5 Desventajas

Como ventaja, he dicho que los modelos lineales viven en su propio universo. La gran cantidad de formas en que puede extender el modelo lineal simple es abrumadora, no solo para principiantes. En realidad, hay múltiples universos paralelos, porque muchas comunidades de investigadores y profesionales tienen sus propios nombres para los métodos que hacen más o menos lo mismo, lo que puede ser muy confuso.

La mayoría de las modificaciones del modelo lineal hacen que el modelo sea menos interpretable. Cualquier función de enlace (en un GLM) que no sea la función de identidad complica la interpretación; las interacciones también complican la interpretación; Los efectos de características no lineales son menos intuitivos (como la transformación logarítmica) o ya no se pueden resumir en un solo número (por ejemplo, funciones de spline).

Los GLM, GAM, etc. se basan en suposiciones sobre el proceso de generación de datos. Si se violan, la interpretación de los pesos ya no es válida.

El rendimiento de los conjuntos basados en árboles, árbol de gradiente -gradient tree-, es en muchos casos mejor que los modelos lineales más sofisticados. Esto es en parte mi propia experiencia y en parte las observaciones de los modelos ganadores en plataformas como kaggle.com.

4.3.6 Software

Todos los ejemplos en este capítulo fueron creados usando el lenguaje R. Para los GAM, se utilizó el paquete gam, pero hay muchos otros. R tiene una increíble cantidad de paquetes para extender los modelos de regresión lineal. R alberga más extensiones que cualquier otro lenguaje analítico, abarcando todas las extensiones imaginables del modelo de regresión lineal. Encontrarás implementaciones de p. GAM en Python (como pyGAM), pero estas implementaciones no son tan maduras.

4.3.7 Extensiones adicionales

Como se prometió, aquí hay una lista de problemas que puedes encontrar con los modelos lineales, junto con el nombre de una solución para este problema que puedes copiar y pegar en tu motor de búsqueda favorito.

Mis datos violan el supuesto de ser independientes e idénticamente distribuidos (iid). Por ejemplo, mediciones repetidas en el mismo paciente. Busca modelos mixtos o ecuaciones de estimación generalizadas.

Mi modelo tiene errores heterocedasticos. Por ejemplo, al predecir el valor de una casa, los errores del modelo suelen ser mayores en las casas caras, lo que viola la homocedasticidad del modelo lineal. Busca regresión robusta.

Tengo valores atípicos que influyen fuertemente en mi modelo. Busca regresión robusta.

Quiero predecir el tiempo hasta que ocurra un evento. Los datos de tiempo hasta el evento generalmente vienen con mediciones censuradas, lo que significa que en algunos casos no hubo suficiente tiempo para observar el evento. Por ejemplo, una empresa quiere predecir el fallo de sus máquinas de hielo, pero solo tiene datos durante dos años. Algunas máquinas siguen intactas después de dos años, pero podrían fallar más tarde. Busca modelos de supervivencia paramétricos, regresión de Cox, análisis de supervivencia.

Mi resultado para predecir es una categoría. Si el resultado tiene dos categorías, usa un modelo de regresión logística, que modela la probabilidad de las categorías. Si tienes más categorías, busca regresión multinomial. La regresión logística y la regresión multinomial son dos GLM.

Quiero predecir categorías ordenadas. Por ejemplo, calificaciones escolares. Busca modelo de probabilidades proporcionales.

Mi resultado es un recuento (como el número de hijos en una familia). Busca regresión de Poisson. El modelo de Poisson también es un GLM. También puedes tener el problema de que el valor de recuento de 0 es muy frecuente. Busca regresión de Poisson inflada a cero, modelo de obstáculo.

No estoy seguro de qué características deben incluirse en el modelo para sacar conclusiones causales correctas. Por ejemplo, quiero saber el efecto de un medicamento sobre la presión arterial. El medicamento tiene un efecto directo sobre algún valor sanguíneo y este valor sanguíneo afecta el resultado. ¿Debo incluir el valor sanguíneo en el modelo de regresión? Busca inferencia causal, análisis de mediación.

Me faltan datos. Busca imputación múltiple.

Quiero integrar el conocimiento previo en mis modelos. Busca inferencia bayesiana.

Me siento un poco deprimido últimamente. Busca “Amazon Alexa Gone Wild !!! Versión completa de principio a fin”.