4.4 Árbol de decisión
La regresión lineal y los modelos de regresión logística fallan en situaciones donde la relación entre las características y el resultado es no lineal o donde las características interactúan entre sí. ¡Es hora de brillar para el árbol de decisión! Los modelos basados en árboles dividen los datos varias veces de acuerdo con ciertos valores de corte en las características. A través de la división, se crean diferentes subconjuntos del conjunto de datos, y cada observación pertenece a un subconjunto. Los subconjuntos finales se denominan nodos terminales o de hoja y los subconjuntos intermedios se denominan nodos internos. Para predecir el resultado en cada nodo hoja, se utiliza el resultado promedio de los datos de entrenamiento en este nodo. Los árboles se pueden usar para clasificación y regresión.
Hay varios algoritmos que pueden hacer crecer un árbol. Difieren en la posible estructura del árbol (por ejemplo, número de divisiones por nodo), los criterios de cómo encontrar las divisiones, cuándo detener la división y cómo estimar los modelos simples dentro de los nodos de las hojas. El algoritmo de clasificación y regresión de árboles (CART) es probablemente el algoritmo más popular para la inducción de árboles. Nos centraremos en CART, pero la interpretación es similar para la mayoría de los otros tipos de árboles. Recomiendo el libro ‘Los elementos del aprendizaje estadístico’ (Friedman, Hastie y Tibshirani 2009)17 para una introducción más detallada a CART.
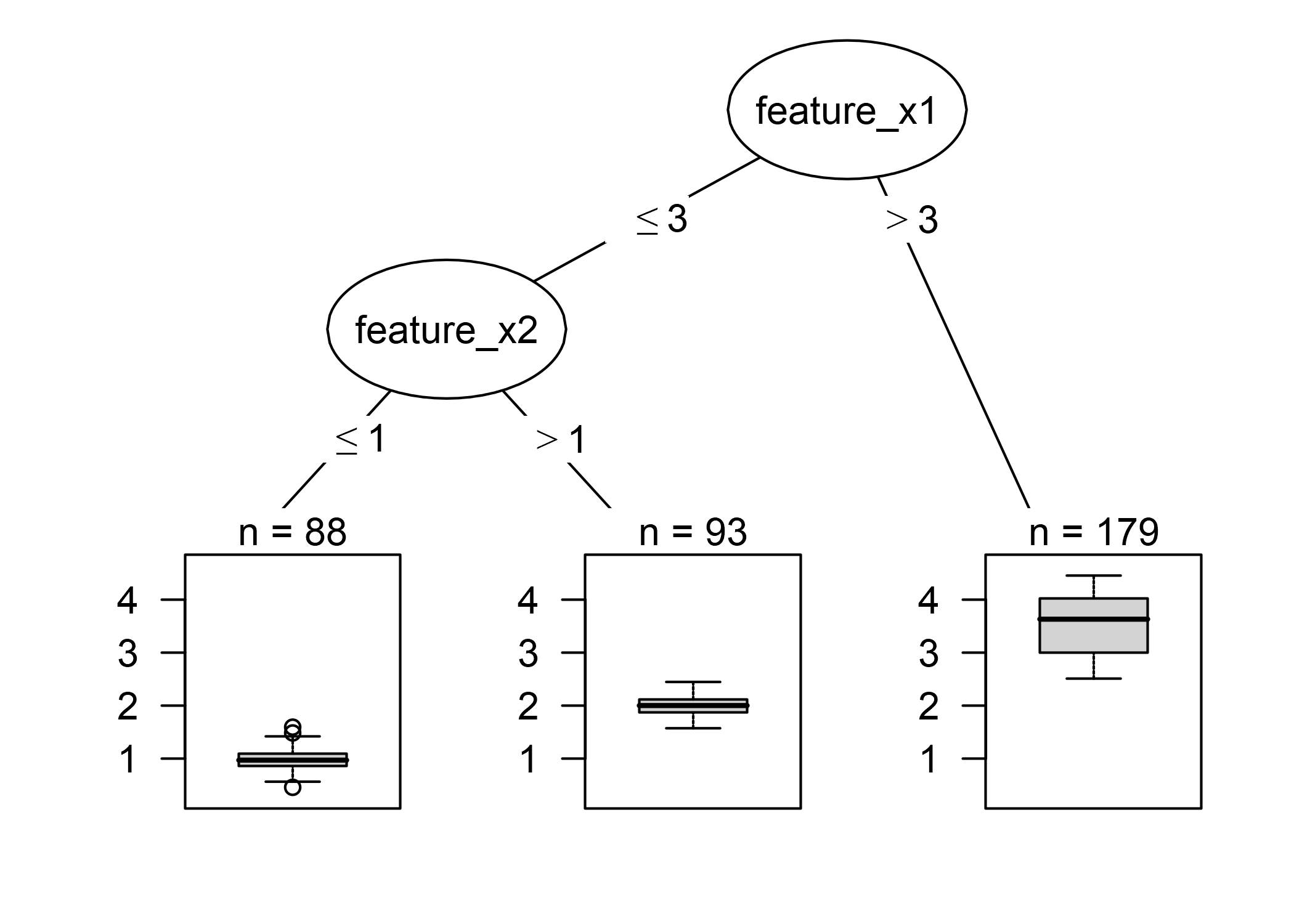
FIGURA 4.15: Árbol de decisión con datos artificiales. Las instancias con un valor mayor que 3 para la característica x1 terminan en el nodo 5. Todas las demás instancias se asignan al nodo 3 o al nodo 4, dependiendo de si los valores de la característica x2 exceden 1.
La siguiente fórmula describe la relación entre el resultado y y las características x.
\[\hat{y}=\hat{f}(x)=\sum_{m=1}^Mc_m{}I\{x\in{}R_m\}\]
Cada instancia cae exactamente en un nodo hoja (= subconjunto \(R_m\)). \(I_{\{x\in{}R_m\}}\) es la función de identidad que devuelve 1 si \(x\) está en el subconjunto \(R_m\) y 0 en caso contrario. Si una instancia cae en un nodo hoja \(R_l\), el resultado previsto es \(\hat{y}=c_l\), donde \(c_l\) es el promedio de todas las instancias de entrenamiento en el nodo hoja \(R_l\).
¿Pero de dónde vienen los subconjuntos? Esto es bastante simple: CART toma una función y determina qué punto de corte minimiza la varianza de Y para una regresión o el índice de Gini de la distribución de clase de Y para clasificación. La varianza nos dice cuánto se distribuyen los valores y en un nodo alrededor de su valor medio. El índice de Gini nos dice cuán “impuro” es un nodo. Si todas las clases tienen la misma frecuencia, el nodo es impuro; si solo hay una clase presente, es completamente puro. La varianza y el índice de Gini se minimizan cuando los puntos de datos en los nodos tienen valores muy similares para Y. Como consecuencia, el mejor punto de corte hace que los dos subconjuntos resultantes sean lo más diferentes posible con respecto al resultado objetivo. Para las características categóricas, el algoritmo intenta crear subconjuntos probando diferentes agrupaciones de categorías. Después de determinar el mejor límite por característica, el algoritmo selecciona la característica para dividir que resultaría en la mejor partición en términos de varianza o índice de Gini y agrega esta división al árbol. El algoritmo continúa esta búsqueda y división recursivamente en ambos nodos nuevos hasta que se alcanza un criterio de detención. Los posibles criterios son: Un número mínimo de instancias que deben estar en un nodo antes de la división, o el número mínimo de instancias que deben estar en un nodo terminal.
4.4.1 Interpretación
La interpretación es simple: Comenzando desde el nodo raíz, vas a los siguientes nodos y los bordes te dicen qué subconjuntos estás mirando. Una vez que llegues al nodo hoja, el nodo te indica el resultado predicho. Todos los bordes están conectados por ‘Y’, lo que significa que las condiciones deben cumplirse simultáneamente.
Plantilla: Si la característica x es [menor / mayor] que el umbral c Y además … entonces el resultado predicho es el valor medio de y de las observaciones en ese nodo.
Importancia de la característica
La importancia general de una característica en un árbol de decisión se puede calcular de la siguiente manera: Revisa todas las divisiones para las que se utilizó la función y mide cuánto ha reducido la varianza o el índice de Gini en comparación con el nodo principal. La suma de todas las importancias se escala a 100. Esto significa que cada importancia puede interpretarse como una parte de la importancia general del modelo.
Descomposición del árbol
Las predicciones individuales de un árbol de decisión pueden explicarse descomponiendo la ruta de decisión en un componente por característica. Podemos rastrear una decisión a través del árbol y explicar una predicción por las contribuciones agregadas en cada nodo de decisión.
El nodo raíz en un árbol de decisión es nuestro punto de partida. Si tuviéramos que usar el nodo raíz para hacer predicciones, predeciría la media del resultado de los datos de entrenamiento. Con la siguiente división, restamos o sumamos un término a esta suma, dependiendo del siguiente nodo en la ruta. Para llegar a la predicción final, debemos seguir la ruta de la instancia de datos que queremos explicar y seguir agregando a la fórmula.
\[\hat{f}(x)=\bar{y}+\sum_{d=1}^D\text{split.contrib(d,x)}=\bar{y}+\sum_{j=1}^p\text{feat.contrib(j,x)}\]
La predicción de una instancia individual es la media del resultado objetivo más la suma de todas las contribuciones de las divisiones D que ocurren entre el nodo raíz y el nodo terminal donde termina la instancia. Sin embargo, no estamos interesados en las contribuciones divididas, sino en las contribuciones de características. Una característica puede usarse para más de una división o para ninguna. Podemos agregar las contribuciones para cada una de las características p y obtener una interpretación de cuánto ha contribuido cada característica a una predicción.
4.4.2 Ejemplo
Echemos otro vistazo a los datos de alquiler de bicicletas. Queremos predecir el número de bicicletas alquiladas en un día determinado con un árbol de decisión. El árbol aprendido se ve así:
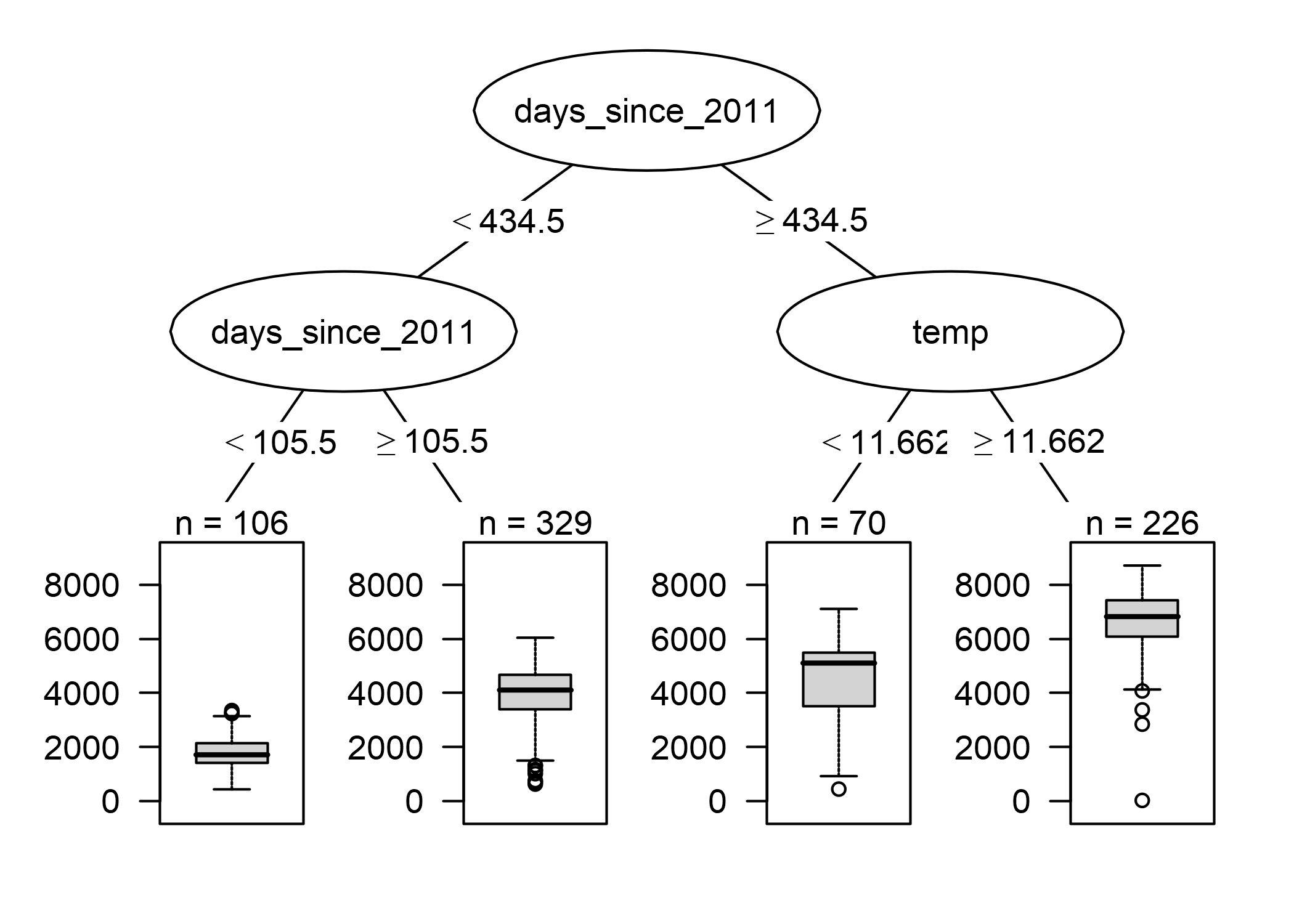
FIGURA 4.16: Árbol de regresión instalado en los datos de alquiler de la bicicleta. La profundidad máxima permitida para el árbol se estableció en 2. La característica de tendencia (días desde 2011) y la temperatura (temperatura) tienen seleccionado para las divisiones. Los diagramas de caja muestran la distribución de los conteos de bicicletas en el nodo terminal.
La primera división y una de las segundas divisiones se realizaron con la función de tendencia, que cuenta los días desde que comenzó la recopilación de datos y cubre la tendencia de que el servicio de alquiler de bicicletas se ha vuelto más popular con el tiempo. Para los días anteriores al día 105, el número previsto de bicicletas es de alrededor de 1800, entre el día 106 y 430 es de alrededor de 3900. Para los días posteriores al día 430, la predicción es 4600 (si la temperatura es inferior a 12 grados) o 6600 (si la temperatura es superior a 12 grados).
La importancia de la característica nos dice cuánto ayudó una característica a mejorar la pureza de todos los nodos. Aquí, se utilizó la regresión, ya que predecir el alquiler de bicicletas es una tarea de regresión.
El árbol visualizado muestra que tanto la temperatura como la tendencia temporal se usaron para las divisiones, pero no cuantifica qué característica fue más importante. La medida de importancia de la característica muestra que la tendencia temporal es mucho más importante que la temperatura.
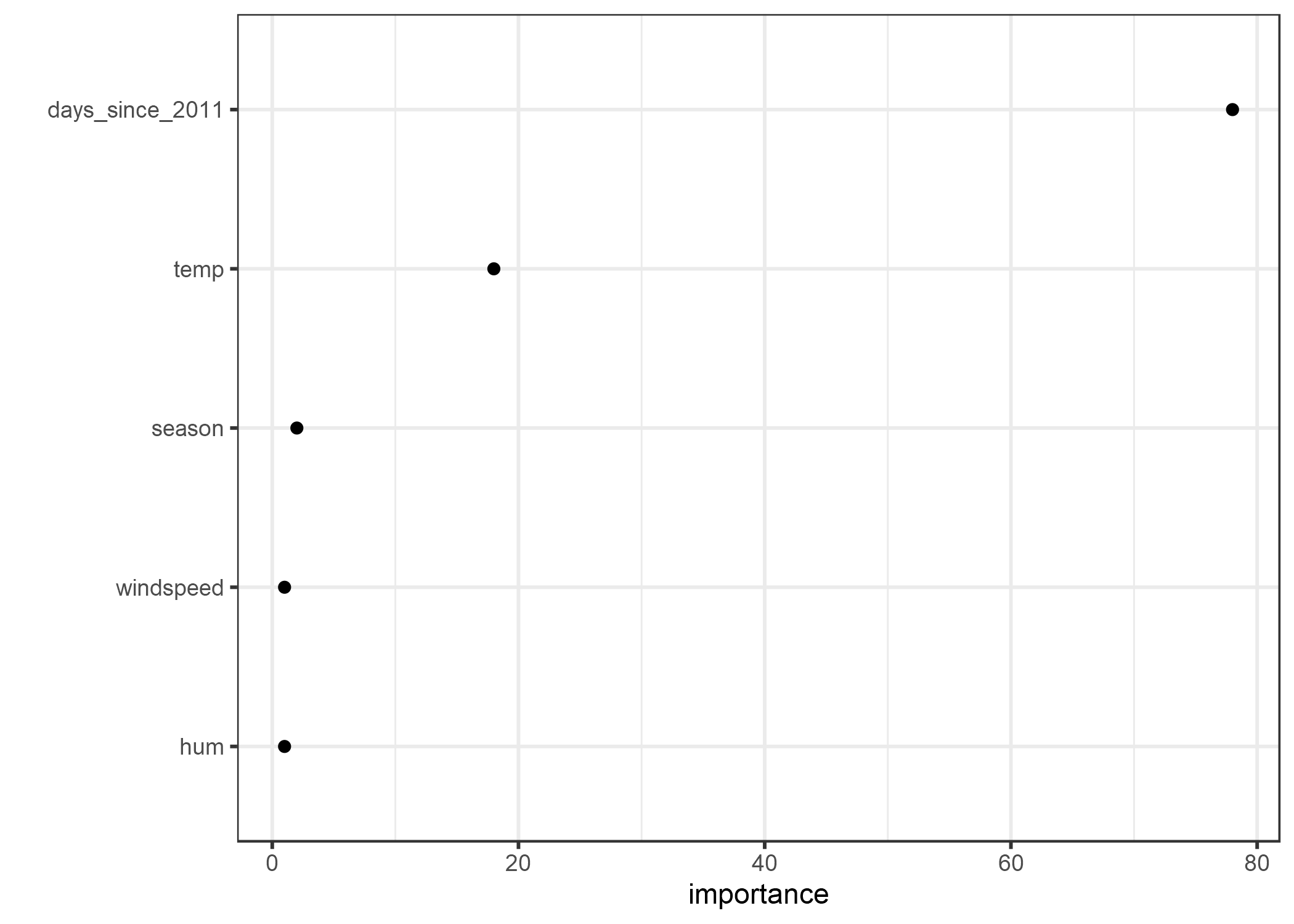
FIGURA 4.17: Importancia de las características medidas por cuánto se mejora la pureza del nodo en promedio.
4.4.3 Ventajas
La estructura de árbol es ideal para capturar interacciones entre características en los datos.
Los datos terminan en grupos distintos que a menudo son más fáciles de entender que los puntos en un hiperplano multidimensional como en la regresión lineal. La interpretación es bastante simple.
La estructura de árbol también tiene una visualización natural, con sus nodos y bordes.
Los árboles crean buenas explicaciones como se define en el capítulo sobre “Explicaciones amigables para los humanos”. La estructura de árbol invita automáticamente a pensar en los valores pronosticados para instancias individuales como contrafactuales: “Si una característica hubiera sido mayor / menor que el punto de división, la predicción habría sido y1 en lugar de y2.” Las explicaciones del árbol son contrastantes, ya que siempre se puede comparar la predicción de una instancia con escenarios relevantes “qué pasaría si” (tal como los define el árbol) que son simplemente los otros nodos de hoja del árbol. Si el árbol es corto (una o tres divisiones de profundidad) las explicaciones resultantes son selectivas. Un árbol con una profundidad de tres requiere un máximo de tres características y puntos divididos para crear la explicación para la predicción de una observación individual. La veracidad de la predicción depende del rendimiento predictivo del árbol. Las explicaciones para los árboles cortos son muy simples y generales, porque para cada división la instancia cae en una u otra hoja, y las decisiones binarias son fáciles de entender.
No hay necesidad de transformar características. En modelos lineales, a veces es necesario tomar el logaritmo de una entidad. Un árbol de decisión funciona igualmente bien con cualquier transformación monotónica de una característica.
4.4.4 Desventajas
Los árboles no pueden lidiar con relaciones lineales. Cualquier relación lineal entre una característica de entrada y el resultado debe ser aproximada por divisiones, creando una función de paso. Esto no es eficiente.
Esto va de la mano con la falta de suavidad. Los cambios leves en la función de entrada pueden tener un gran impacto en el resultado previsto, lo que generalmente no es deseable. Imagina un árbol que predice el valor de una casa y el árbol usa el tamaño de la casa como una de las características divididas. La división ocurre en 100.5 metros cuadrados. Imagina al usuario de un estimador de precios de la vivienda utilizando su modelo de árbol de decisión: Miden su casa, llegan a la conclusión de que la casa tiene 99 metros cuadrados, la ingresan en la calculadora de precios y obtienen una predicción de 200 000 euros. Los usuarios notan que se han olvidado de medir un pequeño trastero con 2 metros cuadrados. El cuarto de almacenamiento tiene una pared inclinada, por lo que no están seguros si pueden contar toda el área o solo la mitad. Entonces deciden probar tanto 100.0 como 101.0 metros cuadrados. Los resultados: la calculadora de precios genera 200.000 euros y 205.000 euros, lo cual es bastante poco intuitivo, porque no ha habido un cambio de 99 metros cuadrados a 100, pero sí de 100 a 101.
Los árboles también son bastante inestables. Algunos cambios en el conjunto de datos de entrenamiento pueden crear un árbol completamente diferente. Esto se debe a que cada división depende de la división principal. Y si se selecciona una característica diferente como la primera característica dividida, la estructura de árbol completa cambia. No crea confianza en el modelo si la estructura cambia tan fácilmente.
Los árboles de decisión son muy interpretables, siempre que sean cortos. El número de nodos terminales aumenta rápidamente con la profundidad. Cuantos más nodos terminales y más profundo sea el árbol, más difícil será comprender las reglas de decisión de un árbol. Una profundidad de 1 significa 2 nodos terminales. Profundidad de 2 significa máx. 4 nodos. Profundidad de 3 significa máx. 8 nodos. El número máximo de nodos terminales en un árbol es 2 a la potencia de la profundidad.
4.4.5 Software
Para los ejemplos de este capítulo, utilicé el paquete rpart R que implementa CART (árboles de clasificación y regresión).
CART se implementa en muchos lenguajes de programación, incluido Python.
Podría decirse que CART es un algoritmo bastante antiguo y algo anticuado y hay algunos algoritmos nuevos e interesantes para ajustar árboles.
Puedes encontrar una descripción general de algunos paquetes R para árboles de decisión en la Vista de tareas CRAN Aprendizaje automático y aprendizaje estadístico bajo la palabra clave Recursive Partitioning.
## Warning in install.packages :
## installation of package '../pkg/sbrl_1.2.tar.gz' had non-zero exit statusFriedman, Jerome, Trevor Hastie, and Robert Tibshirani. “The elements of statistical learning”. www.web.stanford.edu/~hastie/ElemStatLearn/ (2009).↩