4.6 RuleFit
El algoritmo RuleFit de Friedman y Popescu (2008)23 aprende modelos lineales dispersos que incluyen efectos de interacción detectados automáticamente en forma de reglas de decisión.
El modelo de regresión lineal no tiene en cuenta las interacciones entre las características. ¿No sería conveniente tener un modelo que sea tan simple e interpretable como los modelos lineales, pero que también integre interacciones de características? RuleFit llena este vacío. RuleFit aprende un modelo lineal disperso con las características originales y también una serie de características nuevas que son reglas de decisión. Estas nuevas características capturan interacciones entre las características originales. RuleFit genera automáticamente estas características a partir de los árboles de decisión. Cada ruta a través de un árbol se puede transformar en una regla de decisión combinando las decisiones divididas en una regla. Las predicciones de nodo se descartan y solo las divisiones se utilizan en las reglas de decisión:
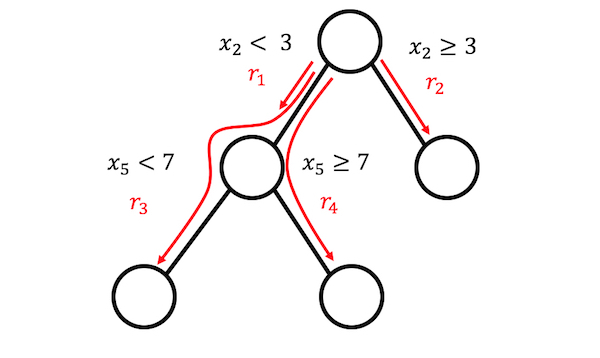
FIGURA 4.20: Se pueden generar 4 reglas desde un árbol con 3 nodos terminales.
¿De dónde vienen esos árboles de decisión? Los árboles están entrenados para predecir el resultado de interés. Esto asegura que las divisiones sean significativas para la tarea de predicción. Cualquier algoritmo que genere muchos árboles se puede usar para RuleFit, por ejemplo, un random forest. Cada árbol se descompone en reglas de decisión que se utilizan como características adicionales en un modelo de regresión lineal disperso (Lasso).
El artículo RuleFit utiliza los datos de vivienda de Boston para ilustrar esto:
El objetivo es predecir el valor medio de la casa de un vecindario de Boston.
Una de las reglas generadas por RuleFit es:
SI número de habitaciones > 6.64 Y concentración de óxido nítrico < 0.67 ENTONCES 1 SI NO 0.
RuleFit también viene con una medida de importancia de características que ayuda a identificar términos lineales y reglas que son importantes para las predicciones. La importancia de la característica se calcula a partir de los pesos del modelo de regresión. La medida de importancia se puede agregar para las características originales (que se utilizan en su forma “bruta” y posiblemente en muchas reglas de decisión).
RuleFit también presenta gráficos de dependencia parcial para mostrar el cambio promedio en la predicción al cambiar una característica. El diagrama de dependencia parcial es un método independiente del modelo que se puede usar con cualquier modelo, y se explica en el capítulo del libro sobre diagramas de dependencia parcial.
4.6.1 Interpretación y ejemplo
Dado que RuleFit estima un modelo lineal al final, la interpretación es la misma que para modelos lineales normales. La única diferencia es que el modelo tiene nuevas características derivadas de las reglas de decisión. Las reglas de decisión son características binarias: Un valor de 1 significa que se cumplen todas las condiciones de la regla; de lo contrario, el valor es 0. Para términos lineales en RuleFit, la interpretación es la misma que en los modelos de regresión lineal: Si la característica aumenta en una unidad, el resultado previsto cambia según el peso de la característica correspondiente.
En este ejemplo, usamos RuleFit para predecir el número de bicicletas alquiladas en un día determinado. La tabla muestra cinco de las reglas generadas por RuleFit, junto con sus pesos e importancias en Lasso. El cálculo se explica más adelante en el capítulo.
| Descripción | Peso | Importancia |
|---|---|---|
| days_since_2011 > 111 & weathersit in (“GOOD”, “MISTY”) | 793 | 303 |
| 37.25 <= hum <= 90 | -20 | 272 |
| temp > 13 & days_since_2011 > 554 | 676 | 239 |
| 4 <= windspeed <= 24 | -41 | 202 |
| days_since_2011 > 428 & temp > 5 | 366 | 179 |
La regla más importante era: “days_since_2011 > 111 & weathersit in (”GOOD“,”MISTY“)” y el peso correspondiente es 793. La interpretación es: Si days_since_2011 > 111 & weathersit in (“GOOD”, “MISTY”), entonces el número predicho de bicicletas aumenta en 793, cuando todos los demás valores de características permanecen fijos. En total, 278 reglas se crearon a partir de las 8 características originales. ¡Bastante! Pero gracias a Lasso, solo 58 de esas 278 tienen un peso diferente de 0.
Calcular la importancia de las características globales revela que la temperatura y la tendencia temporal son las características más importantes:
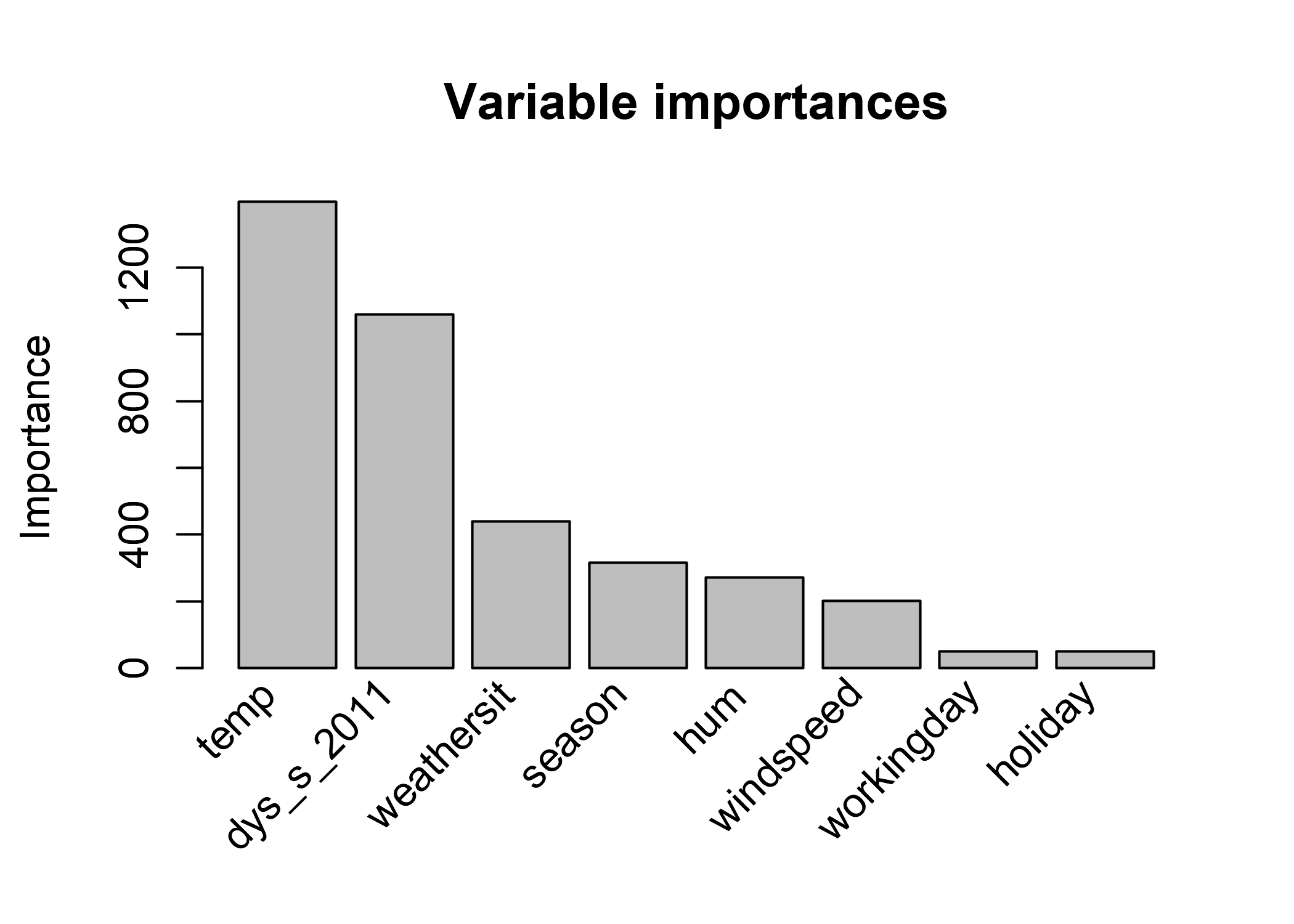
FIGURA 4.21: Importancia de características en un modelo RuleFit que predice cantidad de bicicletas. Las más importantes son la temperatura y la tendencia temporal.
La medición de la importancia de la característica incluye la importancia del término de característica sin procesar y todas las reglas de decisión en las que aparece la característica.
Plantilla de interpretación
La interpretación es análoga a los modelos lineales: El resultado previsto cambia en \(\beta_j\) si la función \(x_j\) cambia en una unidad, siempre que todas las demás funciones permanezcan sin cambios. La interpretación del peso de una regla de decisión es un caso especial: Si se aplican todas las condiciones de una regla de decisión \(r_k\), el resultado previsto cambia en \(\alpha_k\) (el peso aprendido de la regla \(r_k\) en el modelo lineal).
Para la clasificación (usando regresión logística en lugar de regresión lineal): Si se aplican todas las condiciones de la regla de decisión \(r_k\), las probabilidades de evento frente a no evento cambian por un factor de \(\alpha_k\).
4.6.2 Teoría
Profundicemos en los detalles técnicos del algoritmo RuleFit. RuleFit consta de dos componentes: El primer componente crea “reglas” a partir de árboles de decisión y el segundo componente ajusta un modelo lineal con las características originales y las nuevas reglas como entrada (de ahí el nombre “RuleFit”).
Paso 1: generación de reglas
¿Cómo se ve una regla?
Las reglas generadas por el algoritmo tienen una forma simple.
Por ejemplo:
SI x2 < 3 Yx5 < 7 LUEGO 1 SI NO 0.
Las reglas se construyen descomponiendo los árboles de decisión:
Cualquier ruta a un nodo en un árbol se puede convertir en una regla de decisión.
Los árboles utilizados para las reglas se ajustan para predecir el resultado objetivo.
Por lo tanto, las divisiones y las reglas resultantes están optimizadas para predecir el resultado de interés.
Simplemente encadena las decisiones binarias que conducen a un determinado nodo con “Y”, y listo, hay una regla.
Es deseable generar muchas reglas diversas y significativas.
El aumento de gradiente se utiliza para ajustar un conjunto de árboles de decisión al retroceder o clasificar y con sus características originales X.
Cada árbol resultante se convierte en múltiples reglas.
Se puede usar cualquier algoritmo de árboles para generar los de RuleFit.
Un conjunto de árboles se puede describir con esta fórmula general:
\[f(x)=a_0+\sum_{m=1}^M{}a_m{}f_m(X)\]
M es el número de árboles y \(f_m(x)\) es la función de predicción del m-ésimo árbol. Los \(\alpha\) son los pesos. Bagged ensembles, Random forest, AdaBoost y MART producen conjuntos de árboles y se pueden usar para RuleFit.
Creamos las reglas de todos los árboles del conjunto. Cada regla \(r_m\) toma la forma de:
\[r_m(x)=\prod_{j\in\text{T}_m}I(x_j\in{}s_{jm})\]
donde \(\text{T}_{m}\) es el conjunto de características utilizadas en el m-ésimo árbol, I es la función identitaria que es 1 cuando la característica \(x_j\) está en el subconjunto especificado de valores s para la característica j (según lo especificado por las divisiones de árbol) y 0 de lo contrario. Para funciones numéricas, \(s_{jm}\) es un intervalo en el rango de valores de la función. El intervalo se parece a uno de los dos casos:
\[x_{s_{jm},\text{mínimo}}<x_j\]
\[x_j<x_{s_{jm},upper}\]
Las divisiones adicionales en esa característica posiblemente conduzcan a intervalos más complicados. Para las características categóricas, el subconjunto s contiene algunas categorías específicas de la característica.
Un ejemplo inventado para el conjunto de datos de alquiler de bicicletas:
\[r_{17}(x)=I(x_{\text{temp}}<15)\cdot{}I(x_{\text{weather}}\in\{\text{good},\text{cloudy}\})\cdot{}I(10\leq{}x_{\text{windspeed}}<20)\]
Esta regla devuelve 1 si se cumplen las tres condiciones; de lo contrario, 0. RuleFit extrae todas las reglas posibles de un árbol, no solo de los nodos hoja. Entonces, otra regla que se crearía es:
\[r_{18}(x)=I(x_{\text{temp}}<15)\cdot{}I(x_{\text{weather}}\in\{\text{good},\text{cloudy}\}\]
En total, el número de reglas creadas a partir de un conjunto de árboles M con nodos terminales \(t_m\) cada uno es:
\[K=\sum_{m=1}^M2(t_m-1)\]
Un truco introducido por los autores de RuleFit es entrenar árboles con profundidad aleatoria para que se generen muchas reglas diversas con diferentes longitudes. Ten en cuenta que descartamos el valor predicho en cada nodo: solo mantenemos las condiciones que nos llevan a un nodo y luego creamos una regla a partir de él. La ponderación de las reglas de decisión se realiza en el paso 2 de RuleFit.
Otra forma de ver el paso 1: RuleFit genera un nuevo conjunto de características a partir de sus características originales. Estas características son binarias y pueden representar interacciones bastante complejas de sus características originales. Las reglas se eligen para maximizar la tarea de predicción. Las reglas se generan automáticamente a partir de la matriz de covariables X. Simplemente puede ver las reglas como nuevas características basadas en sus características originales.
Paso 2: modelo lineal disperso
Obtienes MUCHAS reglas en el paso 1. Dado que el primer paso puede verse solo como una transformación de características, aún no has terminado de ajustar un modelo. Además, deseas reducir el número de reglas. Además de las reglas, todas tus características “brutas” de su conjunto de datos original también se utilizarán en el modelo lineal disperso. Cada regla y cada característica original se convierte en una característica en el modelo lineal, y por lo tanto obtiene una estimación de peso. Las características originales sin procesar se agregan porque los árboles no pueden representar relaciones lineales simples entre x e y. Antes de entrenar un modelo lineal disperso, clasificamos las características originales para que sean más robustas frente a los valores atípicos:
\[l_j^*(x_j)=min(\delta_j^+,max(\delta_j^-,x_j))\]
donde \(\delta_j^-\) y \(\delta_j^+\) son los cuantiles \(\delta\) de la distribución de datos de la característica \(x_j\). Una opción de \(\delta\) = 0.05 significa que cualquier valor de la característica \(x_j\) que esté en los valores 5% más bajos o 5% más altos se establecerá en los cuantiles en 5% o 95% respectivamente. Como regla general, puedes elegir \(\delta\) = 0.025. Además, los términos lineales deben normalizarse para que tengan la misma importancia previa que una regla de decisión típica:
\[l_j(x_j)=0.4\cdot{}l^*_j(x_j)/std(l^*_j(x_j))\]
\(0.4\) es la desviación estándar promedio de las reglas con una distribución uniforme de \(s_k\sim{}U(0,1)\).
Combinamos ambos tipos de características para generar una nueva matriz de características y entrenar un modelo lineal disperso con Lasso, con la siguiente estructura:
\[\hat{f}(x)=\hat{\beta}_0+\sum_{k=1}^K\hat{\alpha}_k{}r_k(x)+\sum_{j=1}^p\hat{\beta}_j{}l_j(x_j)\]
donde \(\hat{\alpha}\) es el vector de peso estimado para las características de la regla y \(\hat{\beta}\) el vector de peso para las características originales. Dado que RuleFit usa Lasso, la función de pérdida obtiene la restricción adicional que obliga a algunos de los pesos a obtener una estimación cero:
\[(\{\hat{\alpha}\}_1^K,\{\hat{\beta}\}_0^p)=argmin_{\{\hat{\alpha}\}_1^K,\{\hat{\beta}\}_0^p}\sum_{i=1}^n{}L(y^{(i)},f(x^{(i)}))+\lambda\cdot\left(\sum_{k=1}^K|\alpha_k|+\sum_{j=1}^p|b_j|\right)\]
El resultado es un modelo lineal que tiene efectos lineales para todas las características originales y para las reglas. La interpretación es la misma que para los modelos lineales, la única diferencia es que algunas características son ahora reglas binarias.
Paso 3 (opcional): importancia de la característica
Para los términos lineales de las características originales, la importancia de la característica se mide con el predictor estandarizado:
\[I_j=|\hat{\beta}_j|\cdot{}std(l_j(x_j))\]
donde \(\beta_j\) es el peso del modelo con Lasso, y \(std(l_j(x_j))\) es la desviación estándar del término lineal sobre los datos.
Para los términos de la regla de decisión, la importancia se calcula con la siguiente fórmula:
\[I_k=|\hat{\alpha}_k|\cdot\sqrt{s_k(1-s_k)}\]
donde \(\hat{\alpha}_k\) es el peso de Lasso asociado de la regla de decisión y \(s_k\) es el soporte de la característica en los datos, que es el porcentaje de puntos de datos a los que se aplica la regla de decisión (donde \(r_k(x)=0\)):
\[s_k=\frac{1}{n}\sum_{i=1}^n{}r_k(x^{(i)})\]
Una característica ocurre como un término lineal y posiblemente también dentro de muchas reglas de decisión. ¿Cómo medimos la importancia total de una característica? La importancia \(J_j(x)\) de una característica se puede medir para cada predicción individual:
\[J_j(x)=I_l(x)+\sum_{x_j\in{}r_k}I_k(x)/m_k\]
donde \(I_l\) es la importancia del término lineal y \(I_k\) la importancia de las reglas de decisión en las que aparece \(x_j\), y \(m_k\) es el número de características que constituyen la regla \(r_k\). Agregar la importancia de la característica de todas las instancias nos da la importancia de la característica global:
\[J_j(X)=\sum_{i=1}^n{}J_j(x^{(i)})\]
Es posible seleccionar un subconjunto de instancias y calcular la importancia de las características para este grupo.
4.6.3 Ventajas
RuleFit agrega automáticamente interacciones de características a modelos lineales. Por lo tanto, resuelve el problema de los modelos lineales en los que debe agregar términos de interacción manualmente y ayuda un poco con el tema del modelado de relaciones no lineales.
RuleFit puede manejar tareas de clasificación y regresión.
Las reglas creadas son fáciles de interpretar, porque son reglas de decisión binarias. La regla se aplica a una instancia o no. La buena interpretación solo se garantiza si el número de condiciones dentro de una regla no es demasiado grande. Una regla con 1 a 3 condiciones me parece razonable. Esto significa una profundidad máxima de 3 para los árboles en el conjunto de árboles.
Incluso si hay muchas reglas en el modelo, no se aplican a todas las instancias. Para una instancia individual, solo se aplican un puñado de reglas (= tienen pesos distintos de cero). Esto mejora la interpretabilidad local.
RuleFit propone un montón de herramientas de diagnóstico útiles. Estas herramientas son independientes del modelo, por lo que puedes encontrarlas en la sección modelo-agnóstica: importancia de la característica, gráficos de dependencia parcial e interacciones de la característica
4.6.4 Desventajas
A veces, RuleFit crea muchas reglas que obtienen un peso distinto de cero en el modelo Lasso. La interpretabilidad se degrada con el número creciente de características en el modelo. Una solución prometedora es forzar que los efectos de las características sean monótonos, lo que significa que un aumento de una característica tiene que conducir a un aumento de la predicción.
Una anécdota personal: los artículos afirman un buen rendimiento de RuleFit, ¡a menudo cercano al rendimiento predictivo de random forests! pero en los pocos casos en que lo intenté, el rendimiento fue decepcionante. Simplemente pruébalo para tu problema y ve cómo funciona.
El producto final del procedimiento RuleFit es un modelo lineal con características sofisticadas adicionales (las reglas de decisión). Pero dado que es un modelo lineal, la interpretación del peso aún no es intuitiva. Viene con la misma “nota al pie” que un modelo de regresión lineal habitual: “… dado que todas las características son fijas”. Se vuelve un poco más complicado cuando tienes reglas superpuestas. Por ejemplo, una regla de decisión (característica) para la predicción de la bicicleta podría ser: “temp> 10” y otra regla podría ser “temp> 15 & weather = ‘GOOD’”. Si el clima es bueno y la temperatura es superior a 15 grados, la temperatura es automáticamente mayor que 10. En los casos en que se aplica la segunda regla, también se aplica la primera regla. La interpretación del peso estimado para la segunda regla es: “Suponiendo que todas las demás características permanezcan fijas, el número previsto de bicicletas aumenta en \(\beta_2\) cuando el clima es bueno y la temperatura supera los 15 grados”. Pero, ahora queda muy claro que ‘todas las demás características fijas’ son problemáticas, porque si se aplica la regla 2, también se aplica la regla 1 y la interpretación no tiene sentido.
4.6.5 Software y alternativa
El algoritmo RuleFit está implementado en R por Fokkema y Christoffersen (2017)24 y puede encontrar una versión de Python en Github.
Un marco muy similar es skope-rules, un módulo de Python que también extrae reglas de conjuntos. Difiere en la forma en que aprende las reglas finales: Primero, las reglas de skope eliminan las reglas de bajo rendimiento, basadas en los umbrales de recuperación y precisión. Luego, las reglas duplicadas y similares se eliminan al realizar una selección basada en la diversidad de términos lógicos (variable + operador más grande / más pequeño) y el rendimiento (puntaje F1) de las reglas.
Friedman, Jerome H, and Bogdan E Popescu. “Predictive learning via rule ensembles.” The Annals of Applied Statistics. JSTOR, 916–54. (2008).↩
Fokkema, Marjolein, and Benjamin Christoffersen. “Pre: Prediction rule ensembles”. https://CRAN.R-project.org/package=pre (2017).↩